
- •Линейный дифференциальный оператор пространства непрерывных функций. Линейные дифференциальные уравнения и их общее решение.
- •Вронскиан и линейная независимость непрерывных функций
- •3. Матричный метод решения систем дифференциальных уравнений
- •4. Алгебраические действия и их свойства
- •5. Группы и их простейшие свойства
- •6. Подгруппы, определение, критерий, свойства
- •7. Группы подстановок
- •8. Порядок элемента группы
- •9. Порождающие множества в группе. Циклические группы и их свойства.
- •10. Смежные классы по подгруппе и их свойства
- •11. Теорема Лагранжа
- •12. Нормальные делители групп и их свойства
- •13. Факторгруппы
- •14. Гомоморфизмы групп
- •15. Ядро и образ гомоморфизма, и их свойства
- •17. Теорема о строении циклических подгрупп
- •18. Прямое произведение групп. Теорема о строении конечной абелевой группы.
- •19. Действие групп на множестве. Теорема Кэли
- •20. Орбиты элементов. Лемма Бернсайда
- •21. Кольца, определение, примеры и простейшие свойства
- •23. Подкольца, определение, критерий, свойства
- •24. Теорема о минимальном подкольце.
- •32. Теорема о вложимости области целостности в поле
- •33. Абстрактная характеристика алгебраических систем. Абстрактная характеристика кольца целых чисел и поля рациональных чисел
- •36. Алгебры с делением. Алгебра кватернионов. Теорема Фрабениуса
23. Подкольца, определение, критерий, свойства
1)
Подкольцо кольца
—
это пара ![]() ,
где
—
кольцо, а
,
где
—
кольцо, а ![]() — мономорфизм (вложение)
колец. Такое определение согласуется
с общим понятием подобъекта в теории
категорий.
— мономорфизм (вложение)
колец. Такое определение согласуется
с общим понятием подобъекта в теории
категорий.
В
классическом определении подкольцо
кольца ![]() рассматривается
как подмножество
рассматривается
как подмножество ![]() ,
замкнутое относительно операций
и
,
замкнутое относительно операций
и ![]() из
основного кольца.
из
основного кольца.
Примеры
Любой идеал (левый, правый, двусторонний) замкнут относительно сложения и умножения, поэтому является подкольцом в
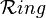 .
.В
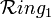 идеал
является подкольцом только тогда, когда
содержит
,
поэтому он обязан совпадать со всем
кольцом. Поэтому в
собственные
идеалы не являются подкольцами.
идеал
является подкольцом только тогда, когда
содержит
,
поэтому он обязан совпадать со всем
кольцом. Поэтому в
собственные
идеалы не являются подкольцами.В подкольцами в являются всевозможные главные идеалы
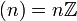 .
В
не
имеет собственных подколец.
.
В
не
имеет собственных подколец.Кольцо целых чисел является подкольцом поля вещественных чисел и подкольцом кольца многочленов
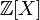 .
.
2) Теорема (критерий подкольца) Подмножество I кольца К является подкольцом тогда и только тогда, когда оно замкнуто относительно вычитания элементов и умножения , т.е. если
(1) (2)
Пусть (где “ ,,- “ быть подкольцом ,,) .Покажем что (1) и (2) имеют место.
Так как , то он является кольцом, а кольцо это абелева група, тогда для , поэтому следовательно (1) выполнено. Выполнимость (2) вытекает из того что I замкнуто относительно умножения.
Пусть , (1),(2) – выполнены. Покажем, что I – подкольцо, т.е. что I – кольцо.
Для этого проверим выполнимость всех аксиом кольца. Из (2) следует, что I – замкнуто относительно умножения, ассоциативность умножения следует из того,что .
Рассмотрим условие (1). Пусть ,но , , ассоциатив -ность сложения вытекает из того что . Таким образом, все аксиомы кольца имеют место в I, следовательно, I – кольцо. Так как , то это подкольцо.
Свойства
подкольца.
Пусть ![]() подкольцо
кольца
подкольцо
кольца ![]() .
Тогда справедливы следующие утверждения:
.
Тогда справедливы следующие утверждения:
1) для
любых элементов ![]() и
и ![]() множества
множества ![]() элементы
элементы ![]() и
и ![]() также
принадлежат множеству
;
также
принадлежат множеству
;
2) ноль
и единица кольца
являются
соответственно нулём и единицей
подкольца ![]()
24. Теорема о минимальном подкольце.
тетрадь
25. Идеалы колец
Для кольца идеалом называется подкольцо, замкнутое относительно умножения на элементы из . При этом идеал называется левым(соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из . Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.
Более
точно: Идеалом кольца
называется
такое подкольцо ![]() кольца
,
что
кольца
,
что
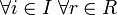 произведение
произведение 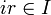 (условие
на правые идеалы);
(условие
на правые идеалы);произведение
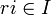 (условие
на левые идеалы).
(условие
на левые идеалы).
Аналогично для полугруппы её идеалом называется подполугруппа, для которой верно какое-нибудь из этих условий (или оба для двустороннего идеала), то же самое и для алгебры.
Свойства:
Левые идеалы в R являются правыми идеалами в т.н. противоположном кольце
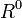 —
кольце с теми же элементами и тем же
сложением, что и данное, но с умножением
определенным
—
кольце с теми же элементами и тем же
сложением, что и данное, но с умножением
определенным 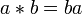 ,
и наоборот.
,
и наоборот.Двусторонние идеалы в кольцах и алгебрах играют ту же роль, что и нормальные подгруппы в группах:
Для всякого гомоморфизма
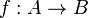 ядром
ядром 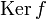 является
идеал, и обратно, всякий идеал — ядро
некоторого гомоморфизма.
является
идеал, и обратно, всякий идеал — ядро
некоторого гомоморфизма.Более того, идеал однозначно (с точностью до изоморфизма) определяет образ гомоморфизма, ядром которого он является:
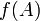 изоморфенфакторкольцу (факторалгебре)
изоморфенфакторкольцу (факторалгебре) 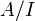 .
.
В кольце целых чисел все идеалы главные и имеют вид
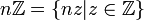 ,
где
,
где 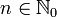 .
.Пересечение идеалов также является идеалом (часто, особенно в коммутативной алгебре, пересечение называется наименьшим общим кратным).
26. Главные идеалы колец
Левый идеал кольца
называется главным
левым идеалом,
если он порождён одним элементом ![]() .
Аналогично определяются главные
правые идеалы и главные
двусторонние идеалы.
.
Аналогично определяются главные
правые идеалы и главные
двусторонние идеалы.
Общепринятых
обозначений для главных идеалов нет.
Иногда используют обозначения ![]() ,
, ![]() ,
, ![]() для
левых, правых и двусторонних главных
идеалов соответственно.
для
левых, правых и двусторонних главных
идеалов соответственно.
Если
—
коммутативное кольцо, то эти три понятия
эквивалентны. В этом случае идеал,
порождённый
,
обозначают через ![]() .
.
Пример:
Все евклидовы
кольца являются
областями главных идеалов; в них для
поиска порождающего элемента данного
идеала можно использовать алгоритм
Евклида.
Вообще, у любых двух главных идеалов
коммутативного кольца есть наибольший
общий делитель в
смысле умножения идеалов; благодаря
этому в областях главных идеалов можно
вычислять (с точностью до умножения на
обратимый элемент) НОД элементов
и
как
порождающий элемент идеала![]() .
.
27. Гомоморфизмы колец, их свойства
1)
Гомоморфизмом
кольца
в
(на) кольцо ![]() называется
отображение
называется
отображение ![]() сохраняющее
главные операции кольца
сохраняющее
главные операции кольца ![]() т.
е. для любых элементов
т.
е. для любых элементов ![]() имеют
место следующие равенства:
имеют
место следующие равенства:
1) ![]()
2) ![]()
3) ![]()
4) ![]() если
если ![]() и
и ![]() существуют.
существуют.
Гомоморфизм кольца на кольцо называется эпиморфизмом.
Эпиморфизм кольца на кольцо называется изоморфизмом, если отображение
 является
инъективным. При этом кольца называются
изоморфными. Факт изомор-физма колец
обозначают записью вида
является
инъективным. При этом кольца называются
изоморфными. Факт изомор-физма колец
обозначают записью вида 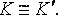
2) Свойства:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]() –
двусторонний идеал кольца K.
–
двусторонний идеал кольца K.
28. Факторкольца
Определение 2.8. Пусть H – двусторонний идеал кольца A, тогда факторкольцом кольца A по идеалу H называется факторгруппа аддитивной
группы кольца по аддитивной группе идеала, на которой определена операция умножения классов смежности по следующему правилу:
(x+H)(y+ H)=xy+ H x.
29. Поле, определение, примеры и простейшие свойства
тетрадь
Множество F с
двумя бинарными операциями
(сложение)
и ![]() (умножение)
называется полем,
если оно образует коммутативную
группупо
сложению
(умножение)
называется полем,
если оно образует коммутативную
группупо
сложению ![]() ,
все его ненулевые элементы образуют
коммутативную группу по умножению
,
все его ненулевые элементы образуют
коммутативную группу по умножению ![]() ,
и выполняется свойство дистрибутивности.
,
и выполняется свойство дистрибутивности.
Свойства:
Характеристика поля всегда
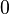 или простое
число.
или простое
число.Поле характеристики содержит подполе, изоморфное полю рациональных чисел .
Поле простой характеристики содержит подполе, изоморфное полю вычетов
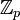 .
.
Количество элементов в конечном поле всегда равно
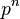 —
степени простого числа.
—
степени простого числа.При этом для любого числа вида существует единственное (с точностью до изоморфизма) поле из элементов, обычно обозначаемое
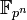 .
.
Любой ненулевой гомоморфизм полей является вложением.
В поле нет делителей нуля.
Примеры:
— рациональные числа,
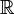 — вещественные
числа,
— вещественные
числа,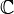 — комплексные
числа,
— комплексные
числа,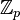 —
поле вычетов по
модулю
,
где
—
простое число.
—
поле вычетов по
модулю
,
где
—
простое число.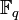 — конечное
поле из
— конечное
поле из 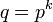 элементов,
где
—
простое число,
—
натуральное.
элементов,
где
—
простое число,
—
натуральное.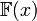 —
поле
рациональных функций вида
—
поле
рациональных функций вида 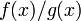 ,
где
,
где 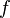 и
—
многочлены над некоторым полем
и
—
многочлены над некоторым полем 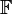 (при
этом
(при
этом 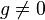 ,
а
и
не
имеют общих делителей, кроме констант).
,
а
и
не
имеют общих делителей, кроме констант).Числа вида
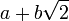 ,
, 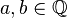 ,
относительно обычных операций сложения
и умножения.
,
относительно обычных операций сложения
и умножения.
30. Подполе, определение, критерий, свойства.
тетрадь
Подполе. Множество M поля P называется подполем P, если оно само является полем при тех же операциях сложения и умножения, которые заданы в поле P. Тогда P называется надполем или расширением поля M.
Так, поле рациональных чисел является подполем поля действительных чисел, а последнее - подполем поля комплексных чисел.

31. Теорема о минимальном подполе
тетрадь
