
- •Линейный дифференциальный оператор пространства непрерывных функций. Линейные дифференциальные уравнения и их общее решение.
- •Вронскиан и линейная независимость непрерывных функций
- •3. Матричный метод решения систем дифференциальных уравнений
- •4. Алгебраические действия и их свойства
- •5. Группы и их простейшие свойства
- •6. Подгруппы, определение, критерий, свойства
- •7. Группы подстановок
- •8. Порядок элемента группы
- •9. Порождающие множества в группе. Циклические группы и их свойства.
- •10. Смежные классы по подгруппе и их свойства
- •11. Теорема Лагранжа
- •12. Нормальные делители групп и их свойства
- •13. Факторгруппы
- •14. Гомоморфизмы групп
- •15. Ядро и образ гомоморфизма, и их свойства
- •17. Теорема о строении циклических подгрупп
- •18. Прямое произведение групп. Теорема о строении конечной абелевой группы.
- •19. Действие групп на множестве. Теорема Кэли
- •20. Орбиты элементов. Лемма Бернсайда
- •21. Кольца, определение, примеры и простейшие свойства
- •23. Подкольца, определение, критерий, свойства
- •24. Теорема о минимальном подкольце.
- •32. Теорема о вложимости области целостности в поле
- •33. Абстрактная характеристика алгебраических систем. Абстрактная характеристика кольца целых чисел и поля рациональных чисел
- •36. Алгебры с делением. Алгебра кватернионов. Теорема Фрабениуса
20. Орбиты элементов. Лемма Бернсайда
1) Подмножество
![]()
называется орбитой элемента ![]() .
.
Действие
группы
на
множестве ![]() определяет
на нём отношение
эквивалентности
определяет
на нём отношение
эквивалентности
![]()
При
этом классами
эквивалентности являются
орбиты элементов. Поэтому, если общее
число классов эквивалентности равно ![]() ,
то
,
то
![]()
где ![]() попарно
неэквивалентны. Для транзитивного
действия
попарно
неэквивалентны. Для транзитивного
действия ![]() .
.
Стабилизаторы [править]
Подмножество
![]()
является подгруппой группы и называется стабилизатором или стационарной подгруппой элемента .
Стабилизаторы
элементов одной орбиты сопряжены, то
есть если ![]() ,
то найдется такой элемент
,
то найдется такой элемент ![]() ,
что
,
что
![]()
Количество элементов в орбите [править]
![]() ,
, ![]() —
стабилизатор элемента
и
—
стабилизатор элемента
и ![]() — индекс
подгруппы
— индекс
подгруппы ![]() ,
в случае конечных
групп равен
,
в случае конечных
групп равен ![]() .
.
Если ![]() ,
то
,
то
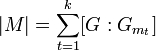 — формула
разложения на орбиты.
— формула
разложения на орбиты.
Эта формула также влечёт следующие тождества:
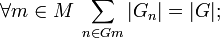
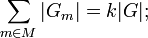
лемма Бёрнсайда.
2) В теории групп лемма Бёрнсайда связывает количество орбит в подгруппе симметрической группы с цикловой структурой элементов этой подгруппы.
Пусть
—
конечная группа, действующая на множестве
.
Для любого элемента ![]() из
будем
обозначать через
из
будем
обозначать через ![]() множество
элементов
,
оставляемых на месте
.
Лемма Бёрнсайда даёт формулу
числа орбит группы
,
обозначаемого
множество
элементов
,
оставляемых на месте
.
Лемма Бёрнсайда даёт формулу
числа орбит группы
,
обозначаемого ![]() :
:
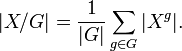
Число орбит (натуральное число или бесконечность) равно среднему количеству точек, оставляемых на месте элементом из .
Док-во:
Доказательство основано на подсчёте числа элементов одного множества двумя способами:
![]()
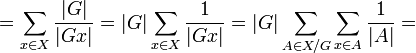
![]()
21. Кольца, определение, примеры и простейшие свойства
Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:
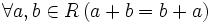 — коммутативность сложения;
— коммутативность сложения;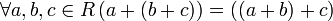 — ассоциативность сложения;
— ассоциативность сложения; —
существование
нейтрального элемента относительно
сложения;
—
существование
нейтрального элемента относительно
сложения;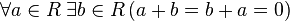 —
существование
противоположного элемента относительно
сложения;
—
существование
противоположного элемента относительно
сложения;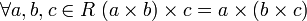 —
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы[1])
—
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы[1])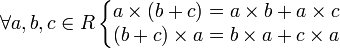 — дистрибутивность.
— дистрибутивность.
Иными
словами, кольцо —
это универсальная
алгебра ![]() ,
такая что алгебра
,
такая что алгебра ![]() — абелева
группа,
и операция
— абелева
группа,
и операция ![]() дистрибутивна слева
и справа относительно
дистрибутивна слева
и справа относительно ![]() .
Кольцо называется ассоциативным,
если операция
ассоциативна.
.
Кольцо называется ассоциативным,
если операция
ассоциативна.
Ассоциативные кольца могут обладать следующими дополнительными свойствами:
наличие единицы:
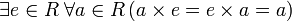 (кольцо
с единицей);
(кольцо
с единицей);коммутативность умножения:
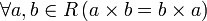 (коммутативное
кольцо);
(коммутативное
кольцо);отсутствие делителей нуля:
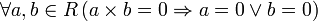 (целостное
кольцо или область
целостности).
(целостное
кольцо или область
целостности).
Кольца, для которых выполнены два последние свойства, называются целостными (иногда также областями целостности или просто областями, хотя условие коммутативности не всегда считается обязательным).
Иногда под ассоциативным кольцом понимают ассоциативное кольцо с единицей. Но имеются примеры ассоциативных колец без единицы, например — нулевое кольцо, кольцо чётных чисел, или же любой несобственный идеал в кольце. Рассматриваются также неассоциативные кольца без единицы, например лиевские кольца и др.
Если умножение в данном кольце коммутативно, то принято называть его коммутативным кольцом.
Простейшие свойства:
Пусть ![]() —
кольцо, тогда выполнены следующие
свойства:
—
кольцо, тогда выполнены следующие
свойства:
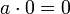 ,
то есть 0 — поглощающий элемент по
умножению.
,
то есть 0 — поглощающий элемент по
умножению.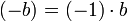 ,
где
,
где 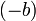 —
элемент, обратный к
—
элемент, обратный к 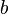 по
сложению.
по
сложению.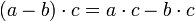
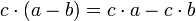
Примеры:
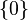 —
тривиальное
кольцо, состоящее из одного нуля. Это
единственное кольцо, в котором ноль
является мультипликативной единицей.
Считать этот тривиальный пример кольцом
важно с точки зрения теории
категорий,
так как при этом в категории колец
возникает нулевой объект, через который
пропускается любой нулевой гомоморфизм
колец.
—
тривиальное
кольцо, состоящее из одного нуля. Это
единственное кольцо, в котором ноль
является мультипликативной единицей.
Считать этот тривиальный пример кольцом
важно с точки зрения теории
категорий,
так как при этом в категории колец
возникает нулевой объект, через который
пропускается любой нулевой гомоморфизм
колец.— целые числа (с обычным сложением и умножением). Это важнейший пример кольца, так как любое кольцо можно рассматривать как алгебру над
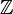 .
.— кольцо вычетов по модулю натурального числа n. Это классические примеры колец из теории чисел. Они являются полями тогда и только тогда, когда число простое. Соответствующие поля являются отправной точкой для построения теории конечных полей. Кольца вычетов также важны при исследовании структуры конечнопорождённых абелевых групп, Их также можно использовать для построения p-адических чисел.
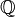 —
кольцо рациональных
чисел,
являющееся полем. Это простейшее
поле характеристики 0.
Оно является основным объектом
исследования в теории чисел. Пополнение
его по всем неэквивалентным нормам
даёт поля вещественных
чисел
—
кольцо рациональных
чисел,
являющееся полем. Это простейшее
поле характеристики 0.
Оно является основным объектом
исследования в теории чисел. Пополнение
его по всем неэквивалентным нормам
даёт поля вещественных
чисел 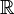 и p-адических
чисел
и p-адических
чисел 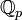 ,
где
—
произвольное простое число.
,
где
—
произвольное простое число.
22. Кольца с сокращением и кольца с единицей
1) Закон существования единичного элемента
![]() ,
,
то кольцо А называется кольцом с единицей.
Замечание. Любое поле является коммутативным кольцом с единицей. Но обратное утверждение является неверным, т.к. не в каждом коммутативном кольце с единицей справедлив закон существования обратного элемента.
Пример. Пусть ![]() —
произвольное множество и
—
произвольное множество и ![]() —
ассоциативное коммутативное кольцо с
единицей. Тогда на
множестве
—
ассоциативное коммутативное кольцо с
единицей. Тогда на
множестве ![]() отображений из
в
возникает
структура ассоциативного коммутативного
кольца с единицей, если положить
отображений из
в
возникает
структура ассоциативного коммутативного
кольца с единицей, если положить
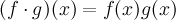 и
и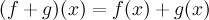 для
всех
для
всех 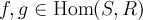 и
и 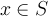 .
.
Мультипликативной
единицей служит постоянное отображение ![]() ,
значение которого есть мультипликативная
единица кольца
,
которое обычно обозначается как
,
значение которого есть мультипликативная
единица кольца
,
которое обычно обозначается как ![]() .
Нулевым элементом служит постоянное
отображение
.
Нулевым элементом служит постоянное
отображение ![]() ,
значение которого есть нулевой
элемент
,
значение которого есть нулевой
элемент ![]() кольца
.
кольца
.
2) Теорема. В кольце без делителей нуля выполняется закон сокращения относительно умножения.
Доказательство.
Пусть А – произвольное кольцо без
делителей нуля, a, b,![]() –
его произвольные элементы и
выполняется равенство:
–
его произвольные элементы и
выполняется равенство: ![]() .
Тогда
.
Тогда ![]() .
Так как по условию
и
в кольце нет делителей нуля, то
.
Так как по условию
и
в кольце нет делителей нуля, то ![]() .
Таким образом мы доказали, что если
.
Таким образом мы доказали, что если
и
,
то ![]() ,
т.е. выполняется закон сокращения справа.
Аналогично доказывается закон сокращения
слева. Теорема доказана.
,
т.е. выполняется закон сокращения справа.
Аналогично доказывается закон сокращения
слева. Теорема доказана.
Заметим, что в любом кольце выполняется закон сокращения относительно сложения, т.к. кольцо относительно сложения является группой, а в любой группе, как мы видели, справедлив закон сокращения.
