10. Смежные классы по подгруппе и их свойства

Пусть G – группа и H – ее собственная подгруппа, т.е.  . Тогда существует  . Тогда множество   называется левым смежным классом группы G по подгруппе H, порожденное элементом a.

Свойства смежных классов:

Доказательство: 

aH и bH – либо полностью совпадают, либо полностью не пересекаются.

Доказательство: Пусть  , тогда  .

Рассмотрим  , тогда  , тогда для любого h принадлежащего H:  . Обратное включение очевидно: . Имеем: cH=aH и cH=bH, т.е. смежные классы совпадают.

Все левые смежные классы равны по мощности и эта мощность совпадает с мощностью H. 

Доказательство:

Построим отображение:  . Это отображение сюръективно. Но это отображение инъективно. Если

, т.е. f – биекция. Это значит, что 

Группу G можно представить в виде объединения попарно пересекающихся левых смежных классов.

11. Теорема Лагранжа

Теорема 5.1 (Теорема Лагранжа).

Для любой подгруппы H конечной группы G

|G| = |G : H| |H|.

Доказательство. Каждый класс gH, Hg равномощен подгруппе H, как

показывают взаимнооднозначные соответствия h ↔gh, h ↔hg, h∈H. В

частности, если группа G конечна, то её порядок |G| можно подсчитать,

умножив мощность |H| каждого класса на число |G : H| всех классов. Теорема

доказана.

Следствия:

1. Количество правых и левых смежных классов любой подгруппы   в   одинаково и называется индексом подгруппы   в   (обозначается  ).

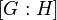2. Порядок любой подгруппы конечной группы   делит порядок  .

3. Из того, что порядок элемента группы равен порядку циклической подгруппы, образованной этим элементом, следует, что порядок любого элемента конечной группы   делит порядок  . Это следствие обобщает теорему Эйлера и малую теорему Ферма в теории чисел.

4. Группа порядка 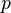 , где   — простое число, циклична. (Поскольку порядок элемента, отличного от единицы, не может быть равен 1, все элементы, кроме единицы, имеют порядок  , и значит, каждый из них порождает группу.)

12. Нормальные делители групп и их свойства

13. Факторгруппы

Пусть   — группа, и   — её нормальная подгруппа. Тогда на классах смежности   в 

можно ввести умножение:

Легко проверить что это умножение не зависит от выбора элементов в классах смежности, то есть если   и  , то  . Это умножение определяет структуру группы на множестве классов смежности, а полученная группа   называется факторгруппой   по  .

Свойства:

• Теорема о гомоморфизме: Для любого гомоморфизма 

,

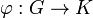
то есть факторгруппа   по ядру   изоморфна её образу   в  .

• Отображение 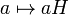  задаёт естественный гомоморфизм  .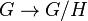

• Порядок   равен индексу подгруппы  . В случае конечной группы   он равен  .

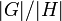• Если   абелева, нильпотентна, разрешима, циклическая или конечнопорождённая, то и   будет обладать тем же свойством.

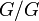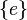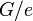•  изоморфна тривиальной группе ( ),   изоморфна  .

Примеры:

• Пусть 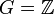 ,  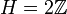, тогда   изоморфна  .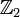

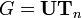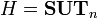• Пусть   (группа невырожденных верхнетреугольных матриц),   (группа верхних унитреугольных матриц), тогда  изоморфна группе диагональных матриц.