
- •Линейный дифференциальный оператор пространства непрерывных функций. Линейные дифференциальные уравнения и их общее решение.
- •Вронскиан и линейная независимость непрерывных функций
- •3. Матричный метод решения систем дифференциальных уравнений
- •4. Алгебраические действия и их свойства
- •5. Группы и их простейшие свойства
- •6. Подгруппы, определение, критерий, свойства
- •7. Группы подстановок
- •8. Порядок элемента группы
- •9. Порождающие множества в группе. Циклические группы и их свойства.
- •10. Смежные классы по подгруппе и их свойства
- •11. Теорема Лагранжа
- •12. Нормальные делители групп и их свойства
- •13. Факторгруппы
- •14. Гомоморфизмы групп
- •15. Ядро и образ гомоморфизма, и их свойства
- •17. Теорема о строении циклических подгрупп
- •18. Прямое произведение групп. Теорема о строении конечной абелевой группы.
- •19. Действие групп на множестве. Теорема Кэли
- •20. Орбиты элементов. Лемма Бернсайда
- •21. Кольца, определение, примеры и простейшие свойства
- •23. Подкольца, определение, критерий, свойства
- •24. Теорема о минимальном подкольце.
- •32. Теорема о вложимости области целостности в поле
- •33. Абстрактная характеристика алгебраических систем. Абстрактная характеристика кольца целых чисел и поля рациональных чисел
- •36. Алгебры с делением. Алгебра кватернионов. Теорема Фрабениуса
7. Группы подстановок
Симметрической
группой множества ![]() называется группа всех перестановок
(то
естьбиекций
называется группа всех перестановок
(то
естьбиекций ![]() )
относительно операции композиции.
)
относительно операции композиции.
Симметрическая
группа множества
обычно
обозначается ![]() .
Если
.
Если ![]() ,
то
также
обозначается через
,
то
также
обозначается через ![]() .
Но если
.
Но если ![]() ,
то
изоморфна
,
то
изоморфна ![]() ,
потому при конечном
,
потому при конечном ![]() считают,
что
равно
.
считают,
что
равно
.
Нейтральным
элементом в
симметрической группе
является тождественная перестановка ![]() ,
определяемая как тождественное
отображение:
,
определяемая как тождественное
отображение:
![]() для
всех
для
всех ![]() .
.
Свойства:
При
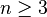 симметрическая
группа
некоммутативна.
симметрическая
группа
некоммутативна.При
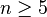 симметрическая
группа
является неразрешимой (и
напротив: при
симметрическая
группа
является неразрешимой (и
напротив: при 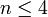 —
разрешимой).
—
разрешимой).В случае, если конечно, число элементов равно
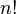 (факториал n),
где
(факториал n),
где 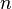 —
число элементов
.
В частности,
—
число элементов
.
В частности, 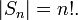
Каждая конечная группа изоморфна некоторой подгруппе группы
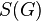 (Теорема
Кэли).
(Теорема
Кэли).Симметрическая группа допускает следующее задание:
![]()
(Можно
считать, что ![]() переставляет
переставляет ![]() и
и ![]() .)
.)
Максимальный порядок элементов группы - функция Ландау.
центр симметрической группы тривиален при .
8. Порядок элемента группы
Пусть ![]() — группа и
— группа и ![]() —
элемент группы.
—
элемент группы.
Определение
1. Говорят,
что ![]() имеет порядок1)
имеет порядок1) ![]() ,
если
,
если ![]() —
наименьшее положительное число такое,
что
—
наименьшее положительное число такое,
что ![]() ,
то есть
,
то есть ![]() .
Если такого положительного
не
существует, то говорят, что
имеет бесконечный
порядок2).
Порядок единичного
элемента
.
Если такого положительного
не
существует, то говорят, что
имеет бесконечный
порядок2).
Порядок единичного
элемента ![]() считается
равным нулю.
считается
равным нулю.
Примеры:
В множестве целых чисел
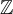 любой
ненулевой элемент имеет бесконечный
порядок.
любой
ненулевой элемент имеет бесконечный
порядок.В группе классов вычетов
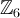 элементы
элементы 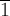 и
и 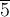 имеют
порядок 6, элементы
имеют
порядок 6, элементы 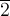 и
и 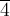 —
порядок 3, элемент
—
порядок 3, элемент 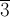 —
порядок 2.
—
порядок 2.
9. Порождающие множества в группе. Циклические группы и их свойства.
1) Порождающее множество группы G (или генератор группы G) - это подмножество S в G, такое что каждый элемент G может быть записан как произведение конечного числа элементов S и их обратных.
Более формально, если S это подмножество группы G, тогда <S>, — подгруппа, порождённая S, — это наименьшая подгруппа в G, содержащая все элементы S, то есть пересечение всех подгрупп, содержащих S. Эквивалентно, <S> это подгруппа всех элементов G, которые могут быть представлены как конечные произведения элементов S и их обратных.
Если G = <S>, говорят, что S порождает G, а элементы S называются порождающими элементами (группы). Если S пусто, то по определению считается <S> = {e}.
2)
В теории
групп группа ![]() называется циклической,
если она может быть порождена одним
элементом a,
то есть все её элементы являются
степенями a (или,
если использовать аддитивную терминологию,
представимы в виде na,
где n — целое
число).
Математическое обозначение:
называется циклической,
если она может быть порождена одним
элементом a,
то есть все её элементы являются
степенями a (или,
если использовать аддитивную терминологию,
представимы в виде na,
где n — целое
число).
Математическое обозначение: ![]() .
.
Несмотря
на своё название, группа не обязательно
должна буквально представлять собой
«цикл». Может случиться так, что все
степени ![]() будут
различными. Порождённая таким образом
группа называется бесконечной
циклической группой и
изоморфна группе целых
чисел по
сложению (
будут
различными. Порождённая таким образом
группа называется бесконечной
циклической группой и
изоморфна группе целых
чисел по
сложению (![]() ).
).
Свойства:
Все циклические группы абелевы.
Каждая конечная циклическая группа изоморфна группе
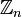 —
— 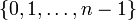 со сложением
по модулю n (её
также обозначают
со сложением
по модулю n (её
также обозначают 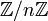 ),
а каждая бесконечная — изоморфна
),
а каждая бесконечная — изоморфна 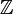 ,
группе целых чисел по сложению.
,
группе целых чисел по сложению.В частности, для каждого натурального числа n существует единственная (с точностью до изоморфизма) циклическая группа порядка n.
Каждая подгруппа циклической группы циклична.
У циклической группы порядка n существует ровно φ(n) порождающих элементов, где φ — функция Эйлера
Если p — простое число, то любая группа порядка p циклическая и единственна с точностью до изоморфизма (это следует из теоремы Лагранжа).
Прямое произведение двух циклических групп порядков и
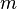 циклично
тогда и только тогда, когда n и m взаимно
просты.
циклично
тогда и только тогда, когда n и m взаимно
просты.Например,
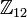 изоморфна
изоморфна 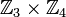 ,
но не изоморфна
,
но не изоморфна 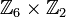 .
.
Основная теорема о конечнопорождённых абелевых группах утверждает, что любая конечнопорождённая абелева группа единственным образом разлагается в прямое произведение примарных циклических групп. Примарной группой может быть циклическая группа
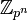 ,
где p —
простое число, или
.
,
где p —
простое число, или
.Мультипликативная группа любого конечного поля является циклической (она порождается элементом поля наибольшего порядка).
Кольцо эндоморфизмов группы изоморфно кольцу . При этом изоморфизме числу r соответствует эндоморфизм , который сопоставляет элементу сумму r его экземпляров. Такое отображение будет биекцией, если и только если r взаимно просто с n, так что группа автоморфизмов изоморфна
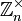 .
.
Примеры:
Группа корней из единицы степени n по умножению.
Группа Галуа любого конечного расширения конечного поля конечна и циклична; обратно, если дано конечное поле F и конечная циклическая группа G, существует конечное расширение F группой Галуа которого будет G.
