Ответы

1. Линейный дифференциальный оператор пространства непрерывных функций. Линейные дифференциальные уравнения и их общее решение.

1) В узком смысле - оператор, действующий на функции, заданные на открытом множестве   и принимающий значения в поле  или   по формуле 

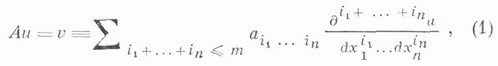
где   - функции со значениями в том же поле, наз. коэффициентами А. Если коэффициенты принимают значения во множестве матриц размера   над полем k, то Л. д. о. А определен на вектор-функциях u=(u₁, ..., u_n).и преобразует их вектор-функции v=(v₁, ..., v_t). Вслучае n=1 он наз. обыкновенным линейным дифференциальным оператором, ав случае n>1 - линейным дифференциальным оператором с частными п. <р оизводными.

2) Опр. Линейным дифференциальным уравнением n-го порядка называется уравнение, в которое неизвестная функция y(x) и её производные входят линейно, т.е. в первой степени:

;

(19)

Если старший коэффициент q₀ (x) отличен от нуля на интервале (a, b), т.е.   для  , то, умножая (19) на  , приводим уравнение к виду со старшим коэффициентом, равным 1:

;

(20)

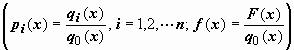; дальше мы будем рассматривать уравнение (20).  Если правая часть уравнения тождественно равна нулю на рассматриваемом интервале (f(x)=0 при  ), то уравнение называется однородным. Таким образом, однородное уравнение - это уравнение вида

;

(21)

Задача Коши для уравнений (20) и (21) ставится также, как и для общего уравнения n-го порядка (17)  : требуется найти решение уравнения (20) или (21), удовлетворяющее начальным условиям

(22)

где y₀, y₁, y₂, …, y_n-1 - заданные числа. Для уравнения (17) теорема существования и единственности решения задачи Коши требовала непрерывности функции   и её производных  ; если привести (20) к виду (17):  ,  то  . Таким образом, условия теоремы Коши приводят к необходимости непрерывности функций f(x) и p_i(x), i = 1, 2, …, n. Далее, вывод теоремы Коши для уравнения (17) заключался в том, что найдётся окрестность точки x₀, в которой существует однозначно определённое решение задачи Коши; для линейных уравнений (20) и (21) вывод более глобален: единственное решение существует на всём интервале (a, b), на котором выполняются условия теоремы: 

2. Вронскиан и линейная независимость непрерывных функций

1) Определитель Вронского (вронскиан).

       Пусть функции   непрерывны вместе с своими производными (до  порядка включительно) на интервале  . Определитель Вронского (вронскиан) указанной системы функций задаётся следующей формулой:

       Для того, чтобы функции   были линейно независимыми на  , достаточно, чтобы   хотя бы в одной точке интервала  . Отметим, что это условие является достаточным, но не необходимым. Т.е., если   для всех значений переменной из интервала  , то про линейную зависимость функций   в общем случае ничего определённого сказать нельзя.

Пусть имеем конечную систему из   функций  , определенных на интервале  . Функции  называют линейно зависимыми на интервале  , если существуют постоянные  , не все равные нулю, такие, что для всех значений  из этого интервала справедливо тождество

2) Если же это тождество выполняется только при  , то функции   называют линейно независимымина интервале  .

Теорема. Если система функций   линейно зависима на отрезке  , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Так, например, система функций   линейно зависима в интервале  , и определитель Вронского этих функций равен нулю всюду в этом интервале (см. примеры 4 и 8).

Эта теорема дает необходимое условие линейной зависимости системы функций. Обратное утверждение неверно, т. е. определитель Вронского может тождественно обращаться в ноль и в том случае, когда данные функции образуют линейно независимую систему на некотором интервале.