Файловый архив студентов. Файловый архив студентов.
1301 вуз, 5075 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Государственный институт экономики, финансов, права и технологий
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
отчет 6.docx
Скачиваний:
1
Добавлен:
01.05.2025
Размер:
284.9 Кб
Скачать
☆
►Содержание►

2. Алгоритм вычислений показателей и экономический анализ полученных результатов

  1. По имеющимся в таблице 1 значениям показателей: A, , g, m, a, φ, K0, L0, используя табличный редактор Excel, рассчитать:

  • по формуле (18) – зависимость X(t);

  • по формуле (9) – зависимость I(t);

  • по формуле (7) – зависимость

  • по формуле (10) – зависимость C(t);

  • по формуле (6) – зависимость L(t), кроме значения L(0)=L0;

  • по формуле: - зависимость K(t), кроме значения K(0)=K0.

Значения t задаём в пределах от 0 до 50 лет с интервалом году. Полученные результаты записаны в таблице 2.

Таблица 2

t

X(t)

I(t)

DK(t)

C(t)

L(t)

K(t)

0

306,03

67,33

52,33

100,99

75,00

750,00

1

324,09

71,30

55,25

106,95

78,45

802,33

2

343,06

75,47

58,32

113,21

82,06

857,58

3

362,97

79,85

61,54

119,78

85,84

915,90

4

383,89

84,45

64,91

126,68

89,79

977,44

5

405,84

89,28

68,44

133,93

93,92

1 042,34

6

428,88

94,35

72,14

141,53

98,25

1 110,78

7

453,07

99,67

76,02

149,51

102,77

1 182,92

8

478,45

105,26

80,08

157,89

107,50

1 258,93

9

505,08

111,12

84,34

166,68

112,45

1 339,01

10

533,02

117,26

88,80

175,90

117,62

1 423,35

11

562,33

123,71

93,47

185,57

123,04

1 512,15

12

593,08

130,48

98,36

195,72

128,70

1 605,62

13

625,33

137,57

103,49

206,36

134,62

1 703,98

14

659,16

145,01

108,86

217,52

140,82

1 807,47

15

694,63

152,82

114,49

229,23

147,30

1 916,34

16

731,83

161,00

120,38

241,50

154,08

2 030,83

17

770,83

169,58

126,56

254,37

161,17

2 151,22

18

811,72

178,58

133,02

267,87

168,59

2 277,77

19

854,59

188,01

139,79

282,02

176,35

2 410,80

20

899,53

197,90

146,89

296,85

184,47

2 550,59

21

946,64

208,26

154,31

312,39

192,96

2 697,48

22

996,02

219,12

162,09

328,69

201,84

2 851,79

23

1 047,77

230,51

170,23

345,76

211,13

3 013,88

24

1 102,01

242,44

178,76

363,66

220,85

3 184,11

25

1 158,85

254,95

187,69

382,42

231,02

3 362,87

26

1 218,41

268,05

197,04

402,08

241,65

3 550,56

27

1 280,83

281,78

206,83

422,67

252,77

3 747,60

28

1 346,22

296,17

217,08

444,25

264,41

3 954,43

29

1 414,74

311,24

227,81

466,86

276,58

4 171,51

30

1 486,52

327,03

239,05

490,55

289,31

4 399,32

31

1 561,73

343,58

250,81

515,37

302,62

4 638,37

32

1 640,51

360,91

263,13

541,37

316,55

4 889,18

33

1 723,03

379,07

276,02

568,60

331,12

5 152,31

34

1 809,48

398,09

289,52

597,13

346,36

5 428,33

35

1 900,03

418,01

303,65

627,01

362,31

5 717,85

36

1 994,87

438,87

318,44

658,31

378,98

6 021,50

37

2 094,20

460,72

333,92

691,08

396,43

6 339,94

38

2 198,23

483,61

350,13

725,41

414,67

6 673,86

39

2 307,18

507,58

367,10

761,37

433,76

7 023,99

40

2 421,27

532,68

384,86

799,02

453,72

7 391,09

41

2 540,76

558,97

403,45

838,45

474,61

7 775,95

42

2 665,87

586,49

422,90

879,74

496,45

8 179,40

43

2 796,89

615,32

443,27

922,97

519,30

8 602,30

44

2 934,08

645,50

464,59

968,25

543,21

9 045,57

45

3 077,72

677,10

486,90

1 015,65

568,21

9 510,16

46

3 228,13

710,19

510,25

1 065,28

594,36

9 997,05

47

3 385,60

744,83

534,69

1 117,25

621,72

10 507,30

48

3 550,47

781,10

560,26

1 171,65

650,34

11 041,99

49

3 723,08

819,08

587,03

1 228,62

680,27

11 602,25

50

3 903,79

858,83

615,05

1 288,25

711,58

12 189,28

Затем, применив «Мастер диаграмм» табличного редактора Excel, строим графики зависимостей: X(t), I(t), C(t), L(t), K(t) (Приложение 1).

  1. Далее используя формулу (23), определяем значение фондовооружённости труда для стационарной траектории а по формуле:

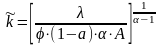(36)

значение фондовооружённости 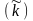при одинаковой скорости роста функций h1(k) и h2(k). Получаем в результате следующие значения: k0= 20,49

  1. На основе ранее полученных данных, рассчитываем и строим функции изменения относительных показателей (Приложение 2):

(37)

Полученные результаты записаны в таблице 3.

Таблица 3

t

k(t)

x(t)

c(t)

i(t)

10,00

4,08

1,35

0,90

10,00

10,23

4,13

1,36

0,91

10,23

10,45

4,18

1,38

0,92

10,45

10,67

4,23

1,40

0,93

10,67

10,89

4,28

1,41

0,94

10,89

11,10

4,32

1,43

0,95

11,10

11,31

4,37

1,44

0,96

11,31

11,51

4,41

1,45

0,97

11,51

11,71

4,45

1,47

0,98

11,71

11,91

4,49

1,48

0,99

11,91

12,10

4,53

1,50

1,00

12,10

12,29

4,57

1,51

1,01

12,29

12,48

4,61

1,52

1,01

12,48

12,66

4,64

1,53

1,02

12,66

12,84

4,68

1,54

1,03

12,84

13,01

4,72

1,56

1,04

13,01

13,18

4,75

1,57

1,04

13,18

13,35

4,78

1,58

1,05

13,35

13,51

4,81

1,59

1,06

13,51

13,67

4,85

1,60

1,07

13,67

13,83

4,88

1,61

1,07

13,83

13,98

4,91

1,62

1,08

13,98

14,13

4,93

1,63

1,09

14,13

14,27

4,96

1,64

1,09

14,27

14,42

4,99

1,65

1,10

14,42

14,56

5,02

1,66

1,10

14,56

14,69

5,04

1,66

1,11

14,69

14,83

5,07

1,67

1,11

14,83

14,96

5,09

1,68

1,12

14,96

15,08

5,12

1,69

1,13

15,08

15,21

5,14

1,70

1,13

15,21

15,33

5,16

1,70

1,14

15,33

15,45

5,18

1,71

1,14

15,45

15,56

5,20

1,72

1,14

15,56

15,67

5,22

1,72

1,15

15,67

15,78

5,24

1,73

1,15

15,78

15,89

5,26

1,74

1,16

15,89

15,99

5,28

1,74

1,16

15,99

16,09

5,30

1,75

1,17

16,09

16,19

5,32

1,76

1,17

16,19

16,29

5,34

1,76

1,17

16,29

16,38

5,35

1,77

1,18

16,38

16,48

5,37

1,77

1,18

16,48

16,57

5,39

1,78

1,18

16,57

16,65

5,40

1,78

1,19

16,65

16,74

5,42

1,79

1,19

16,74

16,82

5,43

1,79

1,19

16,82

16,90

5,45

1,80

1,20

16,90

16,98

5,46

1,80

1,20

16,98

17,06

5,47

1,81

1,20

17,06

17,13

5,49

1,81

1,21

17,13

  1. Определяем величины L(0) по следующей формуле: . Получаем следующее значение L(0)=36,6. Далее изменяем значение L(0) таким образом, чтобы получить выполнение условий: 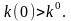Тогда для значение L(0)= 36,6 для значение L(0)> 138,19 для L(0) должно находится в следующем неравенстве 36,6<L(0)< 138,19 и для значение L(0) определяется из следующего неравенства L(0)< 36,6.

Рассчитаем и построим, с применением ТР Excel, функции изменения относительных показателей, используя формулы (37). Графики функции изменения относительных показателей приведены в приложения 3-6.

  1. Рассчитаем коэффициенты фондовооружённости труда 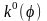для стационарных траекторий при изменении нормы накопления в пределах от 0 до 1 с шагом равным 0,1, используя формулу (23). Тогда получаем:

Таблица 4

φ

к0

0

20,49139

0,1

0,941153

0,2

4,391531

0,3

10,81259

0,4

20,49139

0,5

33,64551

0,6

50,45281

0,7

71,06504

0,8

95,61522

0,9

124,2222

1

156,9938

  1. Для каждого коэффициента фондовооруженности труда k0() и соответствующего ему коэффициента величины нормы накопления рассчитываем значения функций:

  • X(t) по формуле (18);

  • I(t) по формуле (9);

  • по формуле (7);

  • C(t) по формуле (10);

  • K(t) по формуле: ; кроме значения K(0) = K0.

  • L(t) по формуле для выбранного значения φ;

  • k(t) = k0 по формуле ;

  • x(t) = x0 по формуле ;

  • c(t) = c0 по формуле ;

  • i(t) = i0 по формуле .

Значения t задать в пределах от 0 до 10 лет с интервалом году. Вычисления приведены в таблице 5.

Таблица 5

t

X(t)

I(t)

K(t)

C(t)

K(t)

L(t)

k(t)

x(t)

c(t)

i(t)

0

221,59

0,00

-15,00

121,88

750,00

36,60

20,49

6,05

0,00

0,00

1

868,64

47,78

33,08

429,98

735,00

780,96

0,94

1,11

0,55

0,06

2

453,86

49,92

34,56

199,70

768,08

174,90

4,39

2,59

1,14

0,29

3

316,19

52,17

36,12

121,73

802,64

74,23

10,81

4,26

1,64

0,70

4

247,81

54,52

37,74

81,78

838,76

40,93

20,49

6,05

2,00

1,33

5

207,17

56,97

39,44

56,97

876,50

26,05

33,65

7,95

2,19

2,19

6

180,41

59,54

41,22

39,69

915,94

18,15

50,45

9,94

2,19

3,28

7

161,60

62,22

43,07

26,66

957,16

13,47

71,07

12,00

1,98

4,62

8

147,76

65,02

45,01

16,25

1 000,23

10,46

95,62

14,12

1,55

6,21

9

137,25

67,94

47,04

7,55

1 045,24

8,41

124,22

16,31

0,90

8,07

10

129,09

71,00

49,15

0,00

1 092,28

6,96

156,99

18,55

0,00

10,20

  1. На основании результатов вычислений, выполненных в предыдущем пункте, выписываем в отдельную таблицу значения среднедушевого потребления на стационарных траекториях (c0) и соответствующие этим значениям величины нормы накопления (φ).

Полученные результаты представлены в таблице 6

Таблица 6

t

c(t)

0

0

1

0,550575

2

1,141798

3

1,63991

4

1,997911

5

2,186958

6

2,186289

7

1,979669

8

1,553747

9

0,89716

10

0

Затем, используя «Мастер диаграмм» табличного редактора Excel, строим график зависимостей (Приложение 7). Сравнивая величину нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0), с коэффициентом эластичности выпуска по основным производственным фондам (). Значение нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0)=2,2, т.е. коэффициент эластичности выпуска по основным производственным фондам ()=0,4.

8. Рассчитываем и строим, с применением табличного редактора Excel, функцию изменения среднедушевого потребления (c0) от нормы накопления (φ), используя формулу (24). Рассчитанная по формуле (24) норма накопления (φ), приведена в таблице7.

Таблица 7

φ

c0

0

0

0,1

0,550575

0,2

1,141798

0,3

1,63991

0,4

1,997911

0,5

2,186958

0,6

2,186289

0,7

1,979669

0,8

1,553747

0,9

0,89716

1

0

Сравнивая полученные результаты из пунктов 7 и 8 видим, что значения среднедушевой нормы накопления совпадают, что говорит о правильности проведённых расчетов. График функции приведён в приложение 7.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности