2. Задачи, приводящие к теорем Муавра-Лапласа.
Проводится n независимых испытаний, при каждом из которых вероятность наступления события P(А)=р.
1. Чему равна вероятность того, что частота наступления события А отклонится от вероятности р не более чем на α?
.
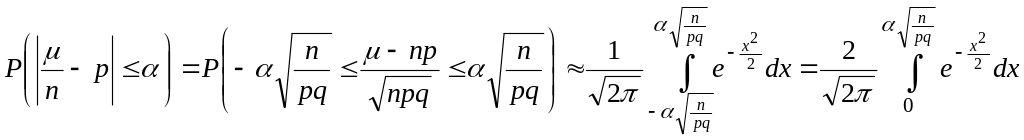2. Какое наименьшее число испытаний нужно произвести для того, чтобы с вероятностью, не меньшей β, частота отклонялась от вероятности не больше чем на α?
Нужно определить
n
из неравенства
.
Вероятность, стоящую в левой части
неравенства, приближённо заменим по
теореме Муавра-Лапласа интегралом. В
результате для определения n
получится неравенство
.
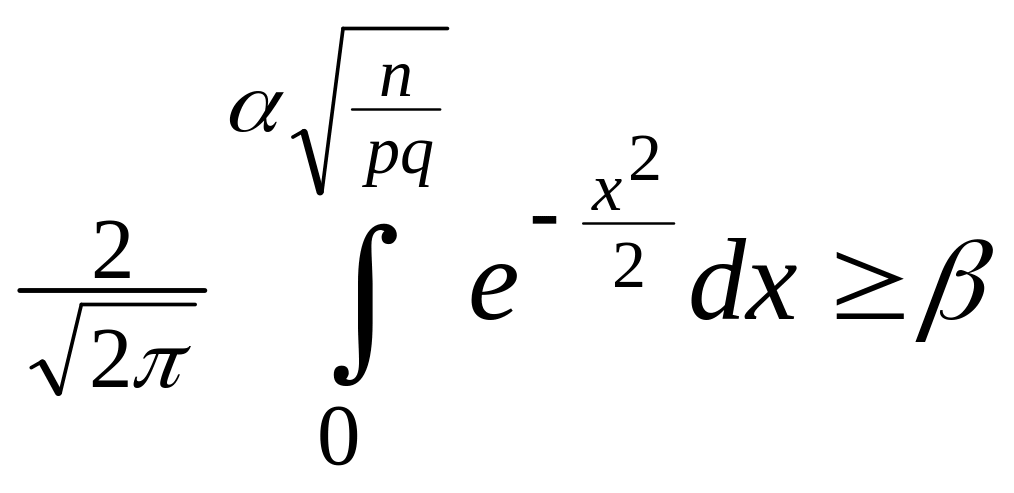3. При данной
вероятности β и числе испытаний n
требуется определить границу возможных
изменений
.
Другими словами, зная β и n,
нужно найти α, для которого
.
Применение интегральной теоремы Лапласа
даёт для определения α уравнение
.
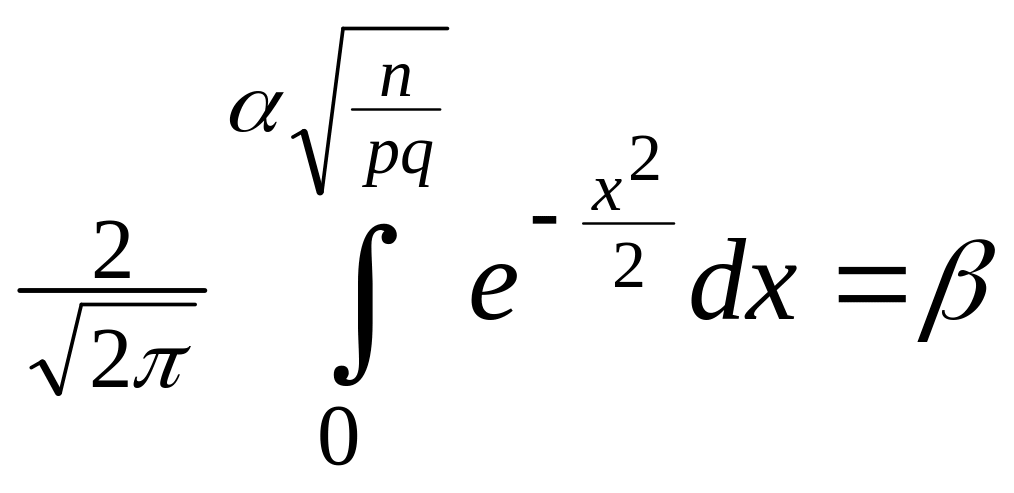Определение.
Функция
называется функцией Лапласа.
Замечание. Так
как
в конечном виде через элементарные
функции не выражается, то для вычисления
,
а также для решения обратной задачи –
вычисления х
по заданному А, используют специальные
таблицы и свойства функции Лапласа.
1. Нечётность.
2. Непрерывность.
3.
.
4. График.
Пример 2. Вероятность изделию некоторого производства оказаться бракованным равна 0б005. Чему равна вероятность того, что из 10000 наудачу взятых изделий бракованных изделий окажется не более 70?
Решение. n=10000, p=0,005. Поэтому по формуле (1) находим вероятность того, что число бракованных изделий окажется не больше 70, равна сумме вероятностей числу бракованных изделий оказаться равным 1, 2, 3, …, 70. Таким образом: .
По интегральной теореме Муавра-Лапласа
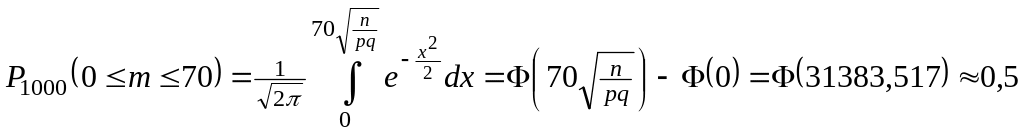
Замечание 1.
Значения (…) в таблице значений функции
Лапласа нет. Все значения, большие 5,
заменяются значением при х=5,
погрешность при этом составляет менее
.
Замечание 2. Если значения р и q не слишком близки к 0 и 1, то интегральная теорема Муавра Лапласа даёт удовлетворительные результаты, но при р и q близких к 0 или 1это представление работает плохо. Для того, чтобы в этом случае теорема Муавра-Лапласа дала хороший результат, требуется, чтобы n было очень велико.
11.4. Теорема Пуассона
Пуассон доказал асимптотическую формулу, приспособленную для малых р.
Теорема Пуассона.
Если в последовательности серий испытаний
события каждой серии взаимно независимы
между собой и имеют каждое вероятность
,
зависящую только от номера серии, а
- число фактически появившихся событий
n-ой
серии, тогда из
следует, что
.
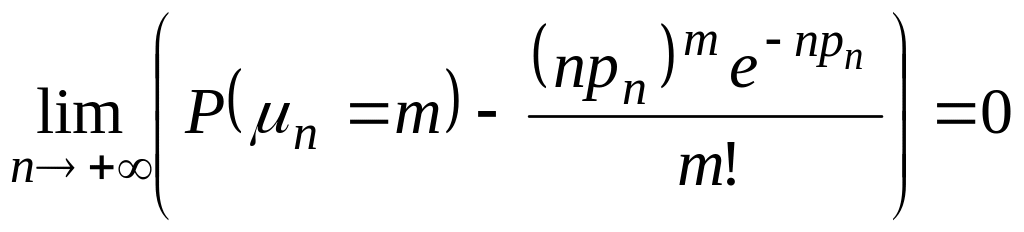Доказательство. См [5, C. 98 – 99].
Обозначим
,
будем предполагать, что эта величина
слабо меняется от серии к серии, обозначим
.
Определение. Распределение вероятностей называется законом Пуассона.
Замечание.
.
Свойства
как функции m.
Рассмотрим отношение
.
Если
,
то
,
если же
,
то
.
Если
,
то
.
Отсюда следует, что величина
возрастает при увеличении m
от 0 до
и при дальнейшем увеличении m
убывает. Если а
– целое число, то
имеет 2 максимальных значения: при
и при
.
Пример. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.