§ 4. Непрерывные цепи маркова
4.1 Основные определения
Определение 1. Марковский случайный процесс с дискретными состояниями и непрерывным временем называется непрерывной цепью Маркова при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.
Примеры: поломки деталей станков и автоматов, поступление вызовов на АТС, приход клиентов к билетным кассам и т.д.
Пусть система
характеризуется
состояниями
,
,
… ,
,
а переход из состояния в состояние может
осуществляться в любой момент времени.
Обозначим через
вероятность того, что в момент времени
система S
будет находиться в состоянии
(
).
Требуется определить для любого
вероятности состояний
,
,
… ,
.
Очевидно, что для любого
.
Для процесса с
непрерывным временем вместо переходных
вероятностей
рассматриваются плотности вероятностей
перехода
.
Определение 2.
Плотностью
вероятности перехода
называется предел отношения вероятности
перехода системы за время
из состояния
в состояние
к длине промежутка
при
:
,
(4.7)
где
– вероятность того, что система,
пребывавшая в момент времени
в состоянии
,
за время
перейдёт из него в состояние
,
при этом всегда
.
Определение 3.
Если плотности вероятностей
,
то процесс называется однородным.
Определение 4.
Если плотности вероятностей зависят
от времени
,
то процесс называется неоднородным.
Замечание. При изучении марковских случайных процессов с дискретными состояниями и непрерывным временем в графе состояний над стрелками, ведущими из состояния в состояние , проставляют соответствующие значения . Такой граф состояний называют размеченным.
Пусть система имеет конечное число состояний , , … , . Случайный процесс, протекающий в этой системе описывается вероятностями состояний , , … , , где – вероятность того, что в момент времени система S будет находиться в состоянии ( ). Требуется определить для любого вероятности состояний , , … , . Для любого . Вероятности состояний находят путём решения системы дифференциальных уравнений (уравнений Колмогорова), имеющих вид:
,
.
(4.8)
Определение 5.
Величина
называется потоком
вероятности перехода из состояния
в состояние
.
Замечание.
Величины
могут быть постоянными или зависеть от
времени. Их также удобно представить в
виде матрицы
.
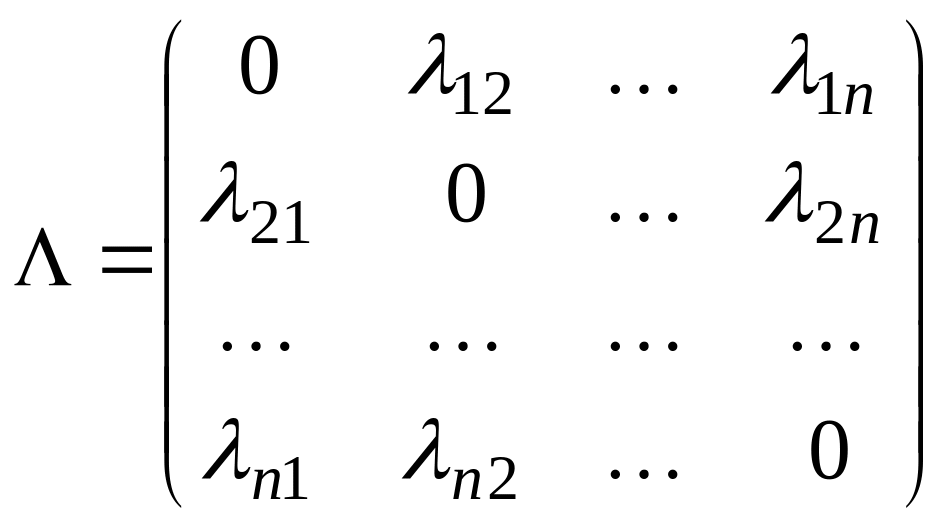Уравнения (4.8) составляют по размеченному графу состояний, пользуясь следующим мнемоническим правилом: производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное ( -е) состояние, минус сумма всех потоков вероятности, идущих из данного ( -го) состояния в другие.
Чтобы решить систему дифференциальных уравнений (4.8), нужно задать начальное распределение вероятностей , , …, .
В случае однородного процесса система (4.8) всегда может быть решена аналитически. В случае неоднородного процесса решение системы (4.8) может быть затруднено. Тогда для решения системы (4.8) применяют, как правило, численные методы.