Особенности матрицы перехода
1.
Каждая строка характеризует выбранное
состояние системы, а её элементы
представляют собой вероятности всех
возможных переходов за один шаг из
выбранного (из
-го)
состояния, в том числе и переход в самое
себя.
2.
Элементы столбцов показывают вероятности
всех возможных переходов системы за
один шаг в заданное (в
-е)
состояние.
Другими словами, строка характеризует вероятность перехода системы из состояния, а столбец – в состояние.
3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий:
,
.
(4.4)
4.
По главной диагонали матрицы переходных
вероятностей стоят вероятности
того, что система не выйдет из состояния
,
а останется в нём.
Теорема 4.1. Если
для однородной марковской цепи заданы
начальное распределение вероятностей
(4.2) и матрица переходных вероятностей
(4.3), то вероятности состояний системы
на
-м
шаге
(
)
определяются по рекуррентной формуле:
(
,
).
(4.5)
Замечание.
Если начальное распределение вероятностей,
распределение вероятностей на
-м
шаге и распределение вероятностей на
-м
представить в виде вектор-столбцов
,
,
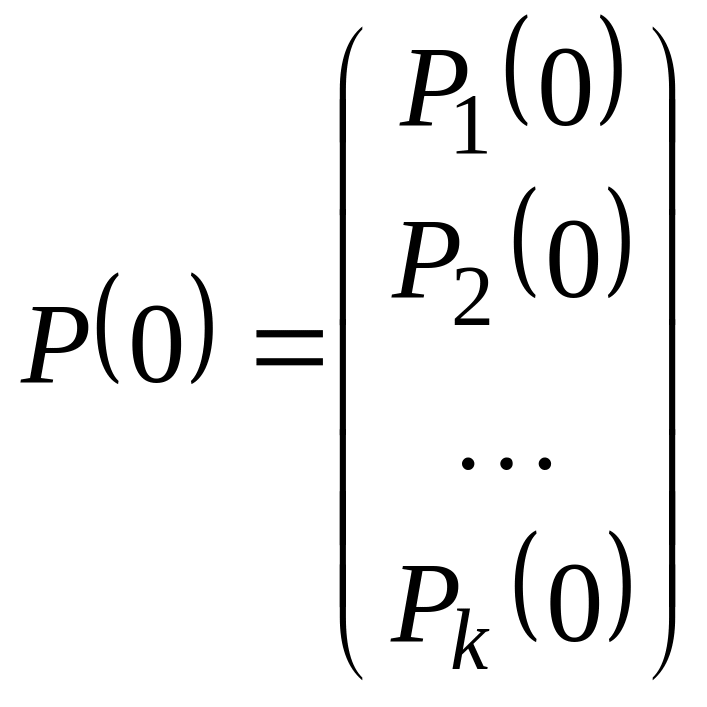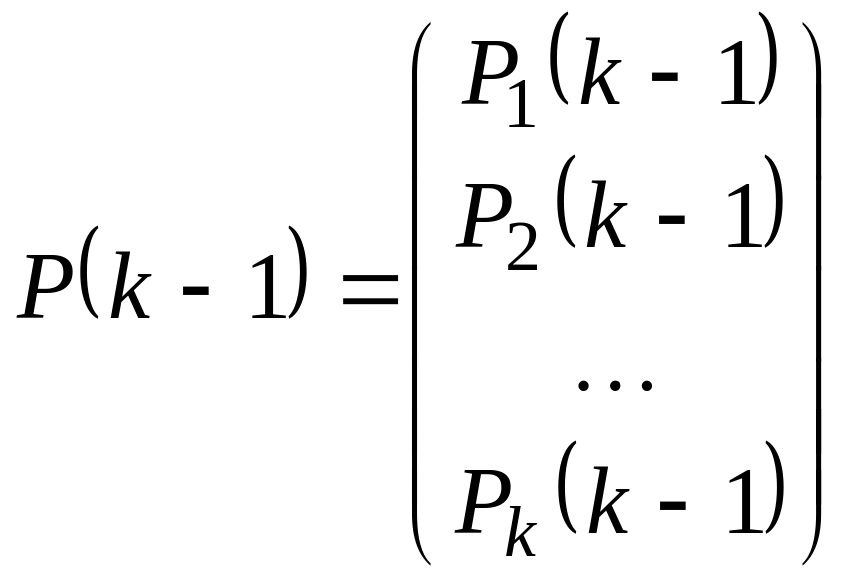соответственно, то рекуррентную формулу
(4.5) можно записать в эквивалентной
матричной форме:
,
(4.5’)
а вектор распределения вероятностей на -м шаге можно вычислить по формуле:
,
(4.6)
Пример 4.1. Пусть автомобиль (система) в течение одной смены (суток) может находиться в одном из двух состояний: исправном ( ) и неисправном ( ). В результате массовых наблюдений за работой автомобиля было выявлено, что в течение суток в 80% случаев автомобиль останется исправным, в 20% случаев сломается, в 90% случаев неисправный автомобиль починят, в 10% случаев поломку устранить не смогут. В начальный момент времени автомобиль был неисправен. Требуется:
1) построить граф состояний системы;
2) составить матрицу вероятностей перехода;
3) определить вероятности состояний автомобиля через трое суток.
Решение. 1) Построим граф состояний системы «автомобиль». Так как система «автомобиль» имеет два состояния – исправен и – неисправен, причём в каждом из состояний она может как задержаться, так и перейти в другое состояние, то граф состояний системы будет иметь:
две вершины – состояния и ;
п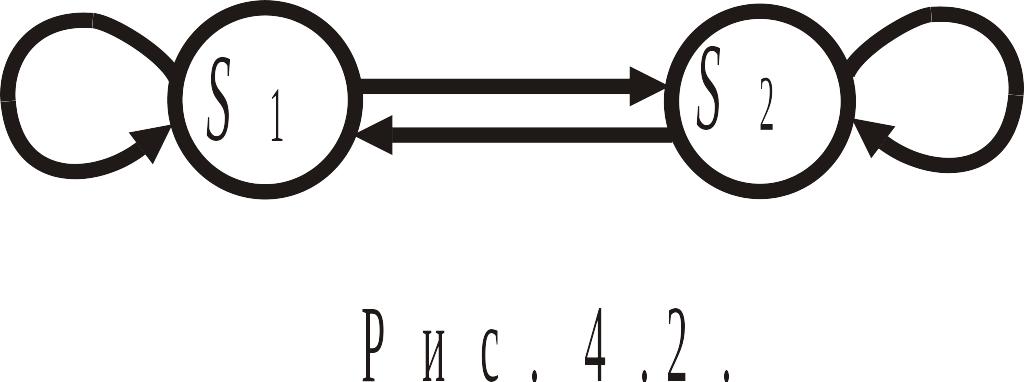
етли
в каждой вершине; петли характеризуют
тот факт, что система может задержаться
в каждом из состояний;
две дуги, соединяющие эти вершины, и характеризующие переход из одного состояния в другое (см. рис. 4.2).
2) Составим матрицу вероятностей перехода.
Так как в течение
суток в 80% случаев автомобиль останется
исправным, то
– вероятность того, что автомобиль
останется в исправном состоянии.
Так как в течение
суток в 20% случаев автомобиль сломается,
то
– вероятность того, что автомобиль
перейдёт из состояния «исправен» в
состояние «неисправен».
Так как в течение
суток в 90% случаев неисправный автомобиль
починят, то
– вероятность того, что автомобиль
перейдёт из состояния «неисправен» в
состояние «исправен».
Так как в течение
суток в 10% случаев поломку устранить не
смогут, то
– вероятность того, что автомобиль
задержится в состоянии «неисправен».
Таким образом, матрица вероятностей
перехода примет вид:
.
3) Найдём распределение
вероятностей состояний автомобиля
через трое суток (
).
Так как в начальный момент времени
автомобиль был неисправен, то
,
и начальное распределение вероятностей
автомобиля имеет вид:
.
Тогда по формуле (4.6) имеем
.
Ответ. После третьих суток автомобиль будет находиться в исправном состоянии с вероятностью 0,819 и в состоянии «неисправен» с вероятностью 0,181.