3.Характеризація вагових систем голосування

_{Вище ми навели необхідну умову для того, щоби система голосування була ваговою. Побудуємо приклад, який показує, що умова стійкості до обмінів не є достатньою для того, щоб система голосування була ваговою. Справді, нехай м} , причому вважаємо, що деяка підмножина з трьох елементів, скажімо, є меншиною з правом вето: рішення приймається, якщо за нього проголосує не менше п’яти учасників голосування, у тім не менше двох представників меншини. Очевидно, що така система стійка до обмінів. Нижче ми сформулюємо сильнішу, ніж умова стійкості до обмінів. Насамперед розгляньмо довільні дві коаліції 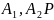_{і нехай , .}

_{Вважаймо}

, .

Перехід від до і називається торгівлею. Зауважмо, що при торгівлі коаліції обмінюються не обов’язково однаковою кількістю учасників.

Означення 3.1. Система голосування називається k – стійкою до торгівлі, де k - деяке натуральне число ,якщо не існує k виграшних коаліцій,які можна перетворити в k програшних коаліцій за допомогою послідовності торгівель. Система голосування називається стійкою до торгівлі, якщо вона є k- стійкою до торгівлі для кожного натурального k.

Теорема 3.2. Для системи голосування S на n-елементній множині такі умови еквівалентні:

1. S- вагова система голосування;

2. S- стійка до торгівлі;

3. - стійка до торгівлі.

Доведення. Доведення того, що з умови 1 випливає умова 2, аналогічне доведенню твердження,яке була написано вище. За означенням, з 2 випливає 3.Для того, щоб довести, що з 3 випливає 1, введімо одне поняття, проміжне між ваговою системою голосування та системою голосування - стійкою до торгівлі. Якщо , то функцію назвімо стійкою до торгівлі для , якщо для кожного і кожних послідовностей коаліцій

що задовольняють умови: 1) для кожного ;

2) і ;

3)

4)Для кожного маємо ,

не може бути, що всі коаліції виграшні, а всі коаліції програшні.

Зауважмо, що функція не є стійкою до торгівлі для , то існують послідовності коаліцій

що задовольняють умови 1) – 4), і або не всі коаліції виграшні, або не всі коаліції програшні.

Це означення можна сприймати так: система голосування на множині поводиться як вагова, а на доповненні як стійка до торгівлі, то порожня функція стійка до торгівлі для , а якщо стійка до торгівлі для , то система голосування вагова. Отже , стратегія доведення теореми так. Починаючи з порожньої функції, будуємо елемент за елементом нарощувати її область визначення, тобто доведемо, що якщо стійкою до торгівлі для , то для довільного(фіксованого) елемента таке, що функція стійка до торгівлі для . Для доведення останнього твердження скористаймося такою ідеєю . Якщо ми невдало приписали елементові вагу, то вона завелика, або замала. Покажімо, що нижня грань множини завеликих ваг більша ніж верхня грань множини занизьких ваг, тому залишається свобода для вибору належної ваги. Назвімо число 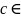замалим, якщо існують послідовності

які показують, що функція не є стійкою до торгівлі і водночас

.

Якщо в цьому означенні замінити у формулі на , то одержимо значення завеликого числа. Доведімо, що якщо число не є ні замалим ні завеликим, то у цьому випадку існують послідовності

,

які показують, що функція не є стійкою до торгівлі і водночас

Вважаймо

, , , ,

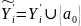тоді для послідовностей

,

Виконано умови 3) і 4) з означення стійкої до торгівлі функції( з заміною та на ) тому одержимо, що функція не є стійкою до торгівлі - суперечність .

Далі доведення розбивається на послідовність тверджень.

1. Якщо дійсне число с занизьке, то існує послідовність, яка це показує і в якій не трапляється в жодному з ,

Справді, маючи дві послідовності, які показують, що с є занизьким значенням, перекиньмо в них з до відпо­відних . Одночасно виберімо таке ж число появ елемен­та серед ; і перемістімо іх до відповідних .

2. Якщо дійсне число с зависоке, то існує послідовність, яка це показує і в якій не трапляється в жодному з .

Доводиться аналогічно до попереднього.

3. Якщо с' < с і с — занизьке значення, то і с' — занизьке значення.

Справді, послідовності, які демонструють, що с — занизь­ке значення, підходять і для с'.

4. Якщо с' > с і с — зависоке значення, то і с' — зависоке значення.

Доводиться аналогічно до попереднього

5. Жодне число не може бути одночасно зависоким і занизьким значенням.

Припустімо протилежне. Нехай с – занизьке значення і

- послідовності, які це

демонструють, причому не трапляється в жодному з . Нехай, крім того, с- зависоке значення і

- послідовності, які це демонструють, причому не зустрічаються в жодному з .Тоді

.

Нехай — і t = Побудуймо нові послідовності коаліцій таким способом. Повторімо кожну ”нештриховану” коаліцію t разів і кожну “нештриховану” коаліцію s разів; цією процедурою одержимо нову послідовність “нештрихованих” коаліцій. Аналогіч­но одержимо нову послідовність “штрихованих” коаліцій. В утворених послідовностях коаліцій елемент трапля­ється st разів серед і жодного разу серед . Також елемент трапляється st разів серед і жодного разу сере . Перекиньмо тепер елемент а₀ від до відпо­відних і від до відповідних . Легко видно, що при цьому зберігається виконання умови 4) з означення стійкої до торгівлі функції. Крім того, зберігається і виконання умови 3), оскільки кожна з сум, що входить до цієї умови зменшується на stc. Зауважмо також, що довжина нових послідовностей коаліцій не перевищує

=

Ми одержали суперечність з тим фактом, що

6. Нехай .

Якщо с' > с, то с не є занизьким значенням. Якщо с'< -с, то с не є зависоким значенням.

Справді, припустімо,що с' > с і с' є занизьким значенням. Тоді існують послідовності

,

які це демонструють, причому не трапляється у жодному з ю за умовою 3),

Оскільки елемент не трапляється а лише серед , маємо

Ця суперечність показує, що с' не є занизьким значенням. Аналогічно доводиться інша частина твердження.

7.Множина занизьких значень обмежена згори, а множина зависоких значень — знизу.

Це випливає з попереднього твердження.

8. Якщо с є верхньою гранню множини занизьких значень то с — занизьке значення.

Припустімо протилежне. Тоді для деякої послідовності значень < ..., що збігається до с, існує єдина для всіх пара послідовностей коаліцій, яка показує , що — занизьке значення, для кожного і .

Оскільки для кожного j нерівність

виконана при , то ця ж нерівність виконана і при .

Звідси випливає, що – занизьке значення.

9. Якщо с є нижньою гранню множини зависоких значень, то с — зависоке значення.

Доведення проходить аналогічно до попереднього.

Для завершення доведення теореми зазначмо, що занизькі значення утворюють замкнений інтервал, обмежений згори, а зависокі значення — замкнений інтервал, обмежений знизу. То­ді залишається непорожній відкритий інтервал для значень, що не є ні зависокими, ні занизькими. □