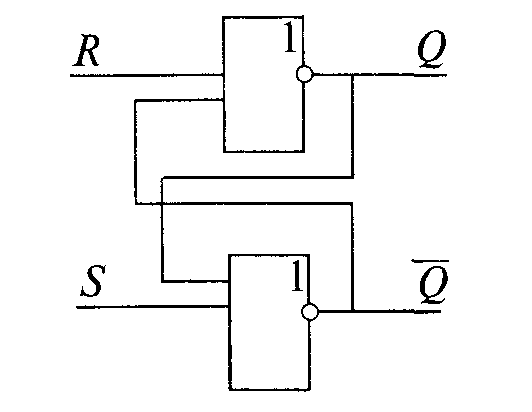
5.12.2. Триггер
Триггером называют узел, способный хранить один разряд двоичного числа. Самый простой триггер — RS. Он состоит из двух элементов ИЛИ—НЕ. Его схема и таблица истинности приведены ниже:
|
Входы
Состояние
Q
R
S
0
0
Q
0
1
1
1
0
0
1
1
Недопустимо |
|||||||||||||||||
Обычно на входы поступают сигналы R = 0 и S = 0, и триггер хранит старое состояние. Если на вход S поступает на короткое время сигнал 1, то триггер переходит в состояние 1, и после того как сигнал S станет равен 0, он будет сохранять это состояние. При подаче 1 на вход R триггер перейдет в состояние 0. Подача на оба входа логической единицы может привести к неоднозначному результату, поэтому такая комбинация входных сигналов запрещена.
Для запоминания 1 байта информации необходимо 8 триггеров, для 1 Кбайта — 8—1024 триггера. Оперативная память современных ЭВМ содержит миллионы триггеров.
В заключение отметим, что ЭВМ состоит из огромного числа отдельных логических элементов, образующих все ее узлы и память.
5.12.3. Дешифратор
Дешифратор — комбинационное устройство, преобразующее комбинацию входных переменных в активный сигнал только на одном из его выходов.
Максимальное количество выходов дешифратора равно 2n, где n – число входов.
Таблица истинности дешифратора
Входы |
Выходы |
||||||
A |
B |
C |
D |
1 |
2 |
3 |
4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
5.12.4. Шифратор
Шифратор (coder) — комбинационное устройство, выполняющее функцию, обратную по отношению к дешифратору, т. е. формирование двоичного кода на выходах при появлении сигнала на одном из входов.
Таблица истинности шифратора
Входы |
Выходы |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |