Введение
Мысль выражать все числа немногими знаками, придавая им значение по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна.
Пьер Симон Лаплас (1749—1827)
Считать приходилось человеку уже очень давно. При этом использовались некоторые вполне определенные способы наименования и записи чисел, то есть определенная система счисления.
Первые приспособления для вычислений облегчали не столько сам процесс счета, сколько запоминание исходных чисел и промежуточных результатов. Числа изображались в привычной цифровой форме в определенной системе счисления (почти всегда — десятичной, которая стала общепризнанной). Такими же были и первые вычислительные машины.
Существует два различных способа изображения чисел в вычислительных машинах и приборах. Первый из них условно называется цифровым. Этот способ реализуется в русских счетах и большом количестве различных приспособлений и машин.
Второй способ изображения чисел называют непрерывным или аналоговым. Здесь для изображения числа применяется некоторая физическая величина, имеющая непрерывный характер. Это может быть длина отрезка или угол поворота вала, ток или напряжение в электрической цепи, температура, давление и другие физические величины. Простейшим примером вычислительного устройства с непрерывным способом изображения чисел является логарифмическая линейка. На ней число изображается длиной отрезка.
Различие в способах представления чисел на русских счетах и логарифмической линейке состоит в физической природе величин. Непрерывные величины, в отличие от цифровых (дискретных) величин, могут принимать любые вещественные значения. Это различие положено в основу классификации вычислительных машин: существуют цифровые (дискретные) машины и аналоговые (непрерывные) машины. Применение того или иного способа изображения чисел диктует свои принципы устройства.
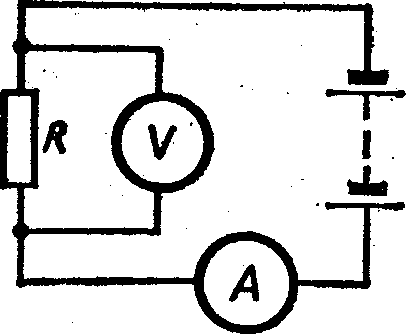
Современные вычислительные машины являются цифровыми и используют электронные элементы. В них используется двоичная система счисления. Если изображать числа с помощью каких-либо электрических величин, то нужно создать электрические схемы, позволяющие выполнять над этими величинами те или иные операции.
Рассмотрим
простой пример схемы, которую можно
использовать для умножения и деления
и в которой числа изображаются
электрическими величинами. Электрическая
цепь состоит из источника, например
гальванической батареи, и резистора.
Известно, что ток такой цепи подчиняется
закону Ома
,
где I
—
ток; Е
—
напряжение
и R
—
сопротивление.
В
Машинные элементы делятся на логические, запоминающие и вспомогательные. Из логических элементов строят операционные схемы, выполняющие арифметические и иные операции. Запоминающие элементы хранят информацию. Вспомогательные элементы предназначены для формирования стандартных сигналов и согласования режимов работы операционных схем. Это деление условно, так как одни и те же элементы могут использоваться различным образом: запоминающий элемент — триггер — может быть построен из логических элементов, а операционная схема — регистр — может рассматриваться как запоминающее устройство.
Результат любой операции, выполняемой в машине, есть двоичное число. Поэтому операционная схема представляет собой функциональный преобразователь, на входах и выходах которого двоичные числа. Для удобства аргументами и значениями функции считают отдельные разряды двоичных чисел. Таким образом, речь идет о переменных и функциях, принимающих лишь значения 0 и 1. Такие переменные и функции носят название логических или булевых функций — по имени английского математика и логика Джорджа Буля (1815—1864) — создателя современной символической логики. Математическая логика, которую называют иногда алгеброй логики, занимается подробным изучением булевых функций.
В данном учебном пособии мы рассмотрим арифметические и логические основы построения вычислительных машин (ВМ).