3. 2. Общий случай условий доминирования

Обобщим результаты, полученные в предыдущем разделе, на слу­чай упорядочений вида (..., t_k, ..., t_r, ...). А именно, определим доста­точные условия того, что неравенство T( ) — T( ) верно для любых расписаний вида = ( , t_k, , t_r, ) и = ( , t_r, , t_k, ).

Теорема 3.2. Для того чтобы упорядочение (..., t_k, ..., t_r, ...) доминировало над упорядочением (..., t_r, ..., t_k, ...), достаточно, что­бы выполнялась система неравенств:

Доказательство. Рассмотрим 5-разбиение:

множества индексов работ = {1, 2, ..., n}. Пусть р¹, р² и р³ - произ­вольные перестановки элементов множеств соответствен­но. Из подпоследовательностей , и и работ сформируем два перестановочных расписания = ( , t_k, , t_r, ) и = ( , t_r, , t_k, ), отличающихся транспозицией элементов и . Расписание предпочтительнее расписания относительно критерия T_max, если верно неравенство

(3.18)

Покажем, что если система неравенств (3.15-3.17) совместна, то неравенство (3.18) верно при любых подпоследовательностях и .

Определим

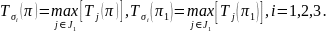
Перепишем неравенство (3.18) в виде

Из очевидного

следует

так что неравенство

эквивалентно неравенству . Из равенства = сле­дует: для того чтобы неравенство было верно для любой подпоследовательности , достаточно выполнения условия

В свою очередь, для того чтобы условие (3.21) было выполнено, дос­таточно, чтобы была непротиворечива система неравенств

Определим условия, при выполнении которых эта система верна для любых подпоследовательностей и .

1. Система неравенств

Очевидно(1.22)⇔ :

Для частичных расписаний и построим мат­рицы и В матрице выделим некоторый критический путь S и разобьем его на четыре сегмента

. Действуя по той же схеме, что и при доказательстве теоремы 3.1, получим, что условия (3.15) являются достаточными для выполнения системы (3.22).

2. Система неравенств

(3.23)

Заметим, как и в п.1,

(1.23)⇔

Пусть - некоторая начальная подпоследовательность в , так что частичные расписания определяют «начальные участки» расписаний и соответственно. Для выполнения усло­вия (3.23) достаточно потребовать:

Исследуя критические пути матрицы и соответствующие пути матрицы и , нетрудно получить

Таким образом, условия (3.16) являются достаточными для выполне­ния (3.23).

3. Система неравенств

(3.24)

Этот случай является обобщением случая 2. Пусть - некоторая начальная подпоследовательность в . Для выполнения условия (3.24) достаточно потребовать:

Проводя рассуждения по аналогии с тем, как это было сделано при доказательстве теоремы об оптимальности транспозиции работ, убеждаемся, что условия (3.17) являются достаточными для выполнения (3.24).

Теорема доказана.