2. Математическая модель

Для нахождения оптимального решения описанной задачи доста­точно исследовать множество (класс) P квазикомпактных перестано­вочных расписаний без искусственных простоев. Перестановоч­ные расписания полностью определяются порядком выполнения ра­бот и в случае n работ задаются одной из n! возможных перестановок их номеров.

Введем следующие обозначения:

1. _n - множество всех перестановок из n элементов 1, 2, ..., n;

2. p(r) - r-й элемент перестановки p ∈ _n.

Перестановке p соответствует упорядочение работ (расписание, перестановочное расписание) (p) = (t_p(1) , t_p(2), , … , t_p(n)) ∈ P. Если p(r) = k, то работа t_k в расписании 𝜋(p) занимает r-е место. Если p(r) = r при всех r = 1, 2, ..., n, то расписание 𝜋 (p) есть (t₁, t₂, ..., t_n).

Обозначим через C_p(r)(𝜋, i) момент завершения выполнения i-й операции (на машине М_i) работы, занимающей в расписании 𝜋 (p) r-е место. Величина определяет момент окончания обра­ботки, то есть длину расписания π.

, будем считать заданными величины (длительность обработки машиной ) и (директивный срок окончания ее выполнения).

Определение 2.1. Разность

называется временным смещением работы .

Определение 2.2.Величина

называется запаздыванием работы в расписании

Критерий оценки расписания есть максимальное временное запаздывание

Задача состоит в нахождении во множестве P перестановочных расписаний такого расписания (оптимального) что

Пусть p – некоторая перестановка элементов 1, 2, …, n. Рассмотрим расписание , соответствующее перестановке p. Директивный срок, запаздывание и временное смещение работы занимающей в расписании -е место, будем обозначать и соответственно.

Для представления расписания используем матричную модель:

Директивные сроки работ , упорядоченных в соответствии с расписанием , будем описывать вектором

2. Условия доминирования

На примере задачи Fm | | C_max было показано, что опре­деление условий доминирования - один из подходов к построению приближенно оптимальных расписаний. Мы проведем аналогичное исследование для конвейерной задачи с директивными сроками Fm | | T_max. При этом будем использовать понятия и опреде­ления, введенные в разделах 1 и 2. Говоря о предпочтительности (доми­нировании) одного множества расписаний перед другим, мы будем иметь в виду критерий T_max - максимальное запаздывание.

Вначале рассмотрим условия, на основании которых можно сде­лать вывод о предпочтительности упорядочения работ вида (..., t_k, t_r, ...) перед упорядочением вида (..., t_r, t_k, ...). Результаты, полученные для упорядочений работ вида (., t_k, t_r, .), мы затем обобщим на случай упорядочений вида (., t_r, ., t_k, .).

3. 1. Доминирование упорядочений вида (..., , , ...) над упорядочениями вида (..., ,...).

Рассмотрим 4-разбиение:

множества индексов работ = {1, 2, ..., n}. Пусть p¹ и p² - произ­вольные перестановки элементов множеств соответственно. Из подпоследовательностей и и работ и сформируем два перестановочных расписания, отличающихся транс­позицией соседних элементов и :

Расписание предпочтительнее расписания в смысле крите­рия T_max, если верно неравенство

Условия доминирования упорядочения работ (..., t_k, t_r, ...) над упорядочением (…, t_r, t_k, ...) будем искать, как решения неравен­ства (3.2), верные при любых и (то есть при всех возможных разбиениях вида (3.1) и перестановках и элементов множеств соответственно).

Замечание 3.1. Говоря обо всех возможных 4-разбиениях ви­да (3.1), мы подразумеваем, что допустимыми, помимо всех прочих, являются специальные случаи:

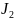1. = ∅, ≠ ∅, то есть E₄( ) = {∅, , {k}, {r}} = { , {k}, {r}}

и

1. ≠∅, = ∅, то есть E₄ = { , ∅, {k}, {r}} = { , {k}, {r}}.

В первом случае расписания и определяются как и , во втором - и .

Для частичных расписаний и в соответствии с выражени­ем (2.3) определим величины максимального запаздывания

Так как

то (1.2) эквивалентно

(3.3)

Очевидно, в оптимальном расписании временные параметры (длительности операций, директивные сроки) любой пары соседних работ t_k и t_r удовлетворяют условию (3.3).

Так как в расписании работа t_k предшествует работе t_r, а в рас­писании работа t_r предшествует работе t_k, то

Отсюда при учете (2.1), (2.2) получаем:

Стало быть, неравенство (3.3) эквивалентно неравенству

(3.4)

Интерес представляют решения последнего неравенства, не зави­сящие от подпоследовательностей и . Так как , то для того чтобы решение неравенства (3.4) было верно для любой подпоследовательности , достаточно выполнения условия

∀ (3.5)

Для получения конструктивного признака оптимальности следует искать решения неравенства (3.5), которые зависят только от пара­метров работ t_k и t_r. Найти такие решения удается лишь в результате сопоставления

1. 

и

2. 

Для выполнения условия (3.5)необходимо потребовать, чтобы для любого было верным хотя бы одно из неравенств

(3.6)

или

(3.7)

Одновременного выполнения неравенств (3.6) и (3.7) достаточно для выполнения условия (3.5). Таким образом, достаточным услови­ем доминирования упорядочения работ (..., t_k, t_r, ...) над упорядоче­нием (., t_r, t_k, .) является

(3.8)

Найдем решения системы (3.8), верные для любых подпоследо­вательностей , и получим условия доминирования в явной форме через параметры работ t_k и t_r.

Из элементов с v-го по w-й векторов A_k и A_r образуем матрицы

Матрица является подматрицей матрицы ( ), = , а - подматрицей ( ), = .

Пусть подпоследовательность (частичное расписание) содержит элементов (| ₁| = ). Построим матрицы ( ), и времен выполнения работ для частич­ных расписаний , и :

1. 

2. 

3. 

По аналогии с введем определители и для матриц , , соответственно.

Рассмотрим первое неравенство системы (3.8) и определим усло­вия, при которых оно верно для всех .Так как

то при учете (2.2) условие

∀ может быть записано в виде:

(3.9)

где и длины частичных расписаний и соответственно. Прини­мая во внимание соотношение представим условие (3.9) в сле­дующей форме:

Зафиксируем подпоследовательность (то есть зафиксируем J₁ и p¹) и рассмотрим критический путь матрицы . Этот путь имеет непустое пересечение с сегментом , которому со­ответствует вектор – -й столбец матрицы :

.

Выделим в критическом пути два сегмента и . Сег­менты имеют общий элемент . Соответствующий элемент матрицы есть a_vk. Очевидно, сегмент является кри­тическим путем матрицы

В частичном расписании работы упорядочены в соответ­ствии с перестановкой индексов p¹ = (p¹, k, r). Поэтому (в силу ра­венства ) для матрицы имеет место:

Рассмотрим теперь частичное расписание , в котором ра­боты упорядочены в соответствии с перестановкой индексов p¹** = (p¹, r, k). В матрице выделим путь , состоящий из сегмента , который содержит те же элементы-клетки, что и сегмент матрицы , и критического пути матрицы . Нетрудно видеть, что

1. 

2. ,

Путь в матрице A не обязательно является критиче­ским. Поэтому

Сопоставляя выражения и , получаем

и

что верно при произвольном и, значит, верно, для любого v = . Отсюда следует, что если система неравенств

совместна, то

и условие (3.10) выполнено.

Таким образом, если система неравенств (3.13) верна, то первое неравенство системы (3.8) справедливо при любой начальной по­следовательности работ .

Перейдем к анализу условия

(второе неравенство системы (3.8)). Пусть - некоторая начальная подпоследовательность в , так что частичные расписания ( t_k, t_r, ) и ( , t_r, t_k, ) определяют «начальные участки» расписа­ний и соответственно. Для выполнения рассматриваемого усло­вия достаточно потребовать, чтобы для любых и выполнялось неравенство

С[( t_k, t_r, ) ,m] ≤ C[( , t_r, t_k, ) ,m].

Будем действовать так же, как при выводе соотношений (3.13). А именно, сопоставим критические пути в матрицах (t_k, t_r),1≤v≤w≤m, и соответствующим им путям в матрицах (t_r, t_k), ( , t_r, t_k) и ( , t_r, t_k, ). Имеем:

Таким образом, доказана следующая теорема.

Теорема 3.1. Для того чтобы упорядочение работ (..., t_k, t_r, ...) доминировало над упорядочением (..., t_r, t_k, ...), достаточно, чтобы выполнялась система неравенств: