2. Распределение электронов у поверхности металла
Движущиеся
из металла электроны проводимости
притягиваются к положительному заряду
ионов, индуцированному на поверхности
металла при выходе электронов, и
возвращаются назад. Около поверхности
образуется облако из вылетающих и
возвращающихся электронов с концентрацией
n(x),
где ось x
перпендикулярна к поверхности металла
и начинается на ней. Получим равновесное
распределение
.
При
используем распределение Больцмана
,
(П.7.12а).
где потенциальная энергия электрона связана с потенциалом точки, где он находится, соотношением
.
Потенциал j(x) создают заряды с объемной плотностью
.
Они связаны уравнением Пуассона, которое в системе СИ
,
где
– электрическая постоянная; ε –
диэлектрическая проницаемость среды
вне металла. Для распределения по оси
x
используем
.
С учетом (П.7.12а) для потенциальной энергии электрона получаем
.
Частное решение уравнения
требует
задания граничных условий на поверхности
металла и вдалеке от него. Используем
,
тогда с учетом (П.7.12а)
,
получаем для заземленного металла
,
.
Напряженность
поля, равная
,
на бесконечности равна нулю, тогда
.
Уравнение
умножаем
на
и интегрируем. Получаем
.
При
учитываем
,
и находим
.
В уравнении
разделяем переменные
,
и интегрируем
.
При
учитываем
,
находим
.
Вводим расстояние экранирования Дебая
,
и получаем
,
.
(П.7.13)
Из (П.7.12а)
и (П.7.13) получаем
.
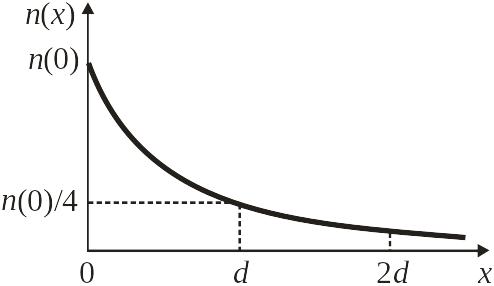
Концентрация
электронов убывает в четыре раза при
.
Расстояние Дебая показывает характерную
протяженность электронного облака у
поверхности металла и имеет величину
порядка ангстрема.
3. Капля жидкости в насыщенном паре
В насыщенном паре образовалась капля жидкости радиусом R. Найти условия увеличения и уменьшения размера капли. Аналогичная задача возникает для квантовой точки, образующейся в насыщенном растворе.
При
образовании капли происходит переход
N
частиц пара в жидкость. Для этого
химический потенциал пара
должен превышать химический потенциал
жидкости
.
При изотермическом и изохорическом
образовании капли система равновесная
при минимуме свободной энергии
.
Из (2.67) с учетом энергии поверхностного
натяжения капли
получаем
,
где
–
площадь поверхности
капли радиусом R;
– коэффициент поверхностного натяжения.
Изменение свободной энергии при образовании капли
,
где
– число частиц
жидкости в капле;
v – объем одной частицы.
Размер капли не меняется в равновесной системе. Это требует экстремума свободной энергии
.
Используем
,
получаем равновесный радиус капли
.
(П.7.16)
С учетом
выполняется
.
Следовательно,
свободная энергия максимальна. Устойчивое
равновесие соответствует минимуму
свободной энергии, поэтому в рассматриваемом
случае
состояние капли неустойчиво:
при
капля увеличивается; при
капля испаряется.
Как изменится состояние капли, если она образуется вокруг иона?