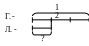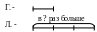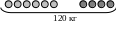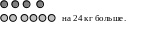Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

Высшего профессионального образования

«Стерлитамакская государственная педагогическая академия имени Зайнаб Биишевой»

Организация самостоятельной работы студентов по изучению курса

«Методика преподавания математики

в начальных классах»

Стерлитамак 2010

УДК 372.8:51(0.7) ББК 74 262.21 М 54

Организация самостоятельной работы студентов по изучению курса «Методика преподавания математики в начальных классах» для студентов 3—6-х курсов заочного отделения по специальности “031200 — Педагогика и методика начального образования” / Сост. Р..3. Мустафина. Стерлитамак. Стерлитамак. гос, пед. академия им. Зайнаб Биишева, 2010. - 120 с.

Пособие представляет собой изложенную в сжатой форме систему подготовки по методике преподавания математики учителей начальных классов. Задания, выполняемые ими по изучению начального курса математики (задания и вопросы к практическим и лабораторным занятиям, задания к контрольным работам, вопросы к экзамену по методике математики, задания исследовательского характера к педагогическим практикам на 4 и 5-м курсах, вопросы к занятиям слецкурса), собраны воедино, образуя целостную картину подготовки будущего учителя начальных классов.

© Составитель: Р.З. Мустафина, 2010 ©  Стерлитамакская государственная педагогическая академия им. Зайнаб Биишевой, 2010.

ВВЕДЕНИЕ

Основная цель пособия к изучению курса “Методика преподавания математики в начальных классах” — оказание помощи в подготовке студентов дневного и заочного отделений к экзамену, к выполнению контрольных работ, выбору темы, направления исследования при написании курсовой и дипломной работы, заданий к педагогической практике.

Пособие состоит из 5 частей:

Введение.

§ 1. Содержание лекций и практических занятий.

§ 2. Задания к выполнению контрольных работ.

§ 3. Задания к педагогической практике.

§ 4. Вопросы к экзамену.

§ 5. Темы курсовых работ.

В конце приводится список основной литературы, используемый при обучении.

В работе реализуется идея интеграции содержания и методов таких дисциплин, как педагогика (раздел дидактики), математика (конкретный смысл арифметических действий и их свойства, вопросы изучения величин и действий с ними, понятие разряда, класса, числа и др.) методика преподавания математики. Осознанное применение общедидактических закономерностей и знаний по вузовскому курсу математики к обучению математике младших школьников, а также мобильность современного учителя в умении анализировать новые подходы в обучении, являются действенным фактором совершенствования профессиональной подготовки будущего учителя. К практическим занятиям предлагаются задания, нацели- / вающие на установление межпредметных связей между названными дисциплинами. За период обучения методике преподавания математики и параллельно за время прохождения педпрактики в качестве учителя начальных классов у каждого. студента будет накоплен материал, куда войдет тематическое планирование, конспекты уроков, фрагменты уроков по отдельным трудным вопросам, методические разработки внеклассных мероприятий, набор дидактических игр, образцы и описание наглядных пособий, конспекты необходимых статей. Тогда каждый студент за годы изучения названного курса подготовит так называемую копилку” для работы с учащимися начальных классов.

К каждой теме указана литература, дополняющая учебники. В том числе предлагаются статьи 1970-80-х годов издания, которые в теоретическом и методическом плане важнее статей последних лет — их студенты могут подобрать самостоятельно, а также воспользоваться имеющимися в кабинете списками литературы к изучаемому курсу.

Содержание лекций и практических занятий

НУМЕРАЦИЯ ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (6 часов)

Тема: Изучение нумерации чисел первого десятка

План:

1. Подготовительный период к теме «Десяток».

1. Основные задачи темы.

2. Последовательность ознакомления с каждым числом.

3. Использование дидактических игр на уроках.

Рекомендательная литература

1. Программа (для 4-летней школы).

1. Жикалкина Т.К. Игровые и занимательные задания по математике: 1-й Кл. – М.: Просвещение, 1986.

2. Король Я.А., Король Я.Р. Изучение нумерации чисел // Начальная школа. – 1987. - №9. – С. 44-47.

3. Кушнерук Е.Н., Медведевская В.Н. Упражнения по составу чисел первого десятка // Начальная школа. – 1979. - №9. – С. 42-45.

4. Кушнерук Е.Н. Письмо цифр // Начальная школа. – 1980. - №9.

5. Семья Ф.Ф. Формирование навыка письма цифр // Начальная школа. – 1990. - № 10. – С. 80-82.

Основные цели изучения нумерации в 1 классе

Программа предусматривает, что в 1 классе дети знакомятся с числами от 1 до 20 (включая 0), причем данный раздел распределен на две самостоятельные темы: «Числа от 1 до 10» (изучается с конца сентября до начала декабря) и «Числа от 11 до 20» (изучается с начала апреля до середины мая).

В процессе изучения темы «Числа от 1 до 10» ребенок усваивает последовательность чисел первого десятка как в прямом, так и в обратном порядке, место каждого числа в натуральном ряду, учится для каждого числа называть предыдущее и непосредственно следующее за ним число, продолжать счет как в прямом, так и в обратном порядке от любого заданного числа. Кроме того, он начинает различать и читать цифры, соотносить цифры, числовые фигуры (далее мы поясним этот термин) и множества конкретных предметов или их изображения в виде иллюстраций.

Важно добиться, чтобы ребенок понимал, как образуется каждое число в пределах десяти из предыдущего числа и единицы, умел сравнивать любые два числа из этого промежутка (без использования знаков «<», «>» и «=»). В ходе изучения этой темы постепенно усваивается состав чисел первого пятка (от 2 до 5), что служит хорошей подготовкой к прочному усвоению арифметических действий. Опишем методику работы над этими вопросами программы.

Счет в прямом и обратном порядке

Как правило уже в дошкольный период дети осваивают счет в пределах десяти. поэтому на данном этапе это умение следует закрепить и развить в том направлении, чтобы счет осуществлялся, начиная не только с единицы или десяти, а с любого, произвольно взятого числа первого десятка. Для этого можно использовать следующий методический прием. Положите на столе 7 кружочков. Попросите ребенка пересчитать их вслух, сопровождая счет показом каждого следующего кружочка. Предложите продолжать счет, начиная с числа 7, сначала в прямом, а затем в обратном порядке. В случае затруднения можно добавлять кружочки (при прямом счете) или убирать их (при обратном счете). Аналогично отрабатывается счет, начиная с любого другого числа первого десятка.

В ходе изучения темы восприятие ребенком количественной стороны предметного мира постепенно абстрагируется. Если первоначально эта сторона рассматривается на примере реальных предметных множеств (карандашей, ручек, тетрадей, книг и т.д.) или соответствующих иллюстраций, то в дальнейшем реальные предметы заменяются числовыми фигурами (карточками с различным количеством кружочков, похожими на домино), а те – цифрами. Приведем пример такого задания.

Соедини каждую цифру с нужной фигурой:

Для того, чтобы ребенок знал место каждого числа в отрезке натурального ряда в пределах десяти, удобно использовать «Кассу цифр и счетного материала» с разрезными цифрами. Попросите его расставить карточки с разрезными цифрами сначала в порядке возрастания, а затем убывания. Опираясь на выстроенный ряд, попросите назвать числа, которые: следуют за числами 3, 6, 9; предшествуют числам 2, 5, 8; являются «соседями» числе 4, 7, 9.

Знакомство с образованием чисел первого десятка

При изучении образования чисел первого десятка целесообразно использовать метод составления возрастающих и убывающих числовых последовательностей. Опишем этот метод.

Ребенку предлагается положить перед собой один кружочек из «Кассы цифр счетного материала», затем добавить еще один такой же кружочек.

• Это действие записывается в кассе с помощью разрезных цифр: 1 + 1 = 2.

• Добавь справа еще один красный кружочек. Сколько теперь стало кружочков? (Три.) Как получили три кружочка? (К двум кружочкам добавили еще один кружочек.) Как это можно записать? (2 + 1 = 3.)

Данная работа продолжается до тех пор, пока не будет получено нужное число:

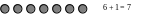
Аналогичным образом строится убывающая числовая последовательность. В этом случае кружочки не добавляются, а убираются:

Методика обучения письму цифр

Методика обучения письму цифр предполагает деление этого процесса на несколько последовательных этапов.

На первом этапе с ребенком подробно разбирается состав цифры (из каких элементов состоит цифра). Например, цифра 4 состоит из трех элементов – палочек, а цифра 3 – из двух правых полуовалов, один из которых (верхний) немного меньше по размеру, чем нижний.

После того, как элементы выделены и проанализированы, можно переходить ко второму этапу, в рамках которого показывается образец написания цифры с подробным комментированием. Проиллюстрируем это на примере цифры 4: «Ставлю ручку немного правее середины верхней стороны клетки и веду ее под наклоном к середине. Затем, не отрывая ручки от бумаги, поворачиваю и веду вправо до правой стороны клетки. Отрываю ручку, ставлю ее немного ниже правого верхнего угла клетки и веду палочку под наклоном к нижней стороне клетки».

На третьем этапе осуществляется «письмо» цифры в воздухе. Ребенок под счет взрослого («раз – и – и – два – и – и – три») пишет цифры в воздухе.

На четвертом этапе отрабатывается письмо цифры на кальке (прозрачной бумаге, под которую помешаются прописных цифр). Кроме кальки можно использовать прописи, в которых ребенок обводит контуры цифры.

На пятом этапе ребенок пишет две-три пробные цифры. Они сравниваются с эталоном и отмечаются те элементы, которые не соответствуют эталону. Порядок написания ошибочно выполненных элементов еще раз проговаривается вместе с ребенком. После этого можно предложить написать одну-две строчки цифры, внимательно следя за правильностью написания, т.к. ошибка может закрепиться.

Сравнение чисел первого десятка

Числа первого десятка сравниваются путем соотнесения соответствующих предметных множеств. Например, нужно сравнить два числа: 4 и 3. для этого ребенку предлагаем положить на стол в одном ряду 4 синих квадрата, а в другом 3 красных так, чтобы каждый квадрат второго ряда лежал под соответствующим квадратом первого ряда:

• Сколько синих квадратов? (Четыре.) Сколько красных квадратов? (Три.) Каких квадратов больше? (Синих.) Значит, - делаем вывод, - четыре больше трех.

• Каких квадратов меньше? (красных.) Значит, три меньше четырех.

Выполнив вместе с ребенком несколько сравнений чисел первого десятка, можно ему предложить самостоятельно найти зависимость между отношениями «больше», «меньше»и расположением сравниваемых чисел в числовом ряду. Дети, как правило, без особого труда подмечают следующую закономерность: если число больше, то оно находится в числовом ряду правее, а если меньше, то левее.

На данном этапе отношения «больше» и «меньше» соответствующими знаками пока не фиксируются. Знаки «>» и «<» вводятся позже, при сравнении чисел второго десятка.

Изучение состава чисел первого пятка (от 2 до 5)

Хорошее знание состава чисел в дальнейшем значительно облегчает усвоение табличных случаев сложения и вычитания однозначных чисел. Если ребенок хорошо может заменять любое число в пределах 10 суммой из двух слагаемых, то у него практически не возникает проблем с выполнением арифметических действий и формированием прочных вычислительных навыков. Поэтому усвоение состава чисел приобретает особое значение.

Работу по изучению состава произвольного числа опишем с помощью следующего примера. Возьмем две тарелки и на одну из них положим 5 яблок. После этого одно яблоко переложим на другую тарелку, сопровождая данное действие следующими вопросами:

1. Сколько яблок в первой тарелке? (Четыре.)

2. Сколько яблок во второй тарелке? (Одно.)

3. Сколько яблок всего в двух тарелках? (Пять.)

4. Значит, пять – это четыре да один.

Вслед за этим еще одно яблоко перекладывается из первой тарелки во вторую. Следуют похожие вопросы, на основе которых делается вывод, что пять – это три да два. И так продолжаем до тех пор, пока все яблоки не переместятся из первой тарелки во вторую.

Все случаи состава числа пять рекомендуется свести в одну таблицу:

5	4	3	2	1
	1	2	3	4

По такому же принципу рассматривается состав остальных чисел. Следует отметить, что по программе четырехлетней начальной школы дети учатся писать цифры несколько позднее, при изучении темы «Сложение и вычитание».

Тема: Методика изучения нумерации

в концентре «Сотня»

План:

1. Задачи и структура темы.

2. Последовательность изучения темы:

а) Числа 11-20.. реализация задач изучения темы на следующих уроках:

- урок ознакомления с новой счетной единицей – десятком;

- уроки устной нумерации

- уроки письменной нумерации.

б) Числа 21-100. Поурочная характеристика реализации основных задач по учебнику математики М-2.

Выполнить задание:

Сделать анализ использования следующих средств наглядности:

- «лента ста»;

- полоски с кружками;

- карточки с разрядными числами.

г) Изучение дидактических игр к теме: Дрозд В.Л. и др. Практикум по методике начального обучения математике: Минский Е.М. От игры к знаниям. – М.: Просвещение, 1982.; Дышинский Е.А. Игротека математического кружка. – М.: Просвещение, 1972.

Нумерация чисел второго десятка (от 11 до 20)

В начале четвертой учебной четверти первоклассники знакомятся с числами второго десятка. В ходе изучения этой темы они усваивают последовательность натуральных числе в пределах 20, учатся читать, записывать и сравнивать эти числа (с использованием знаков «>», «<» и «=»), а также рассматривают десятичный состав двузначных чисел. рассмотрим методику работы над этими вопросами более подробно.

Изучая данную тему, важно показать ребенку процесс образования новой разрядной единицы – десятка. Для этого используются счетные палочки. Отсчитав вместе с ребенком десять палочек, их связывают в пучок и получают новую разрядную единицу - десяток. (Следует отметить, что «десять» и «десяток» - разные понятия. Если «десять» - это десять отдельных единиц, то «десяток» - это десять единиц, объединенных вместе, образующих новую счетную единицу.) Добавляя к десятку отдельные палочки (единицы), получают все остальные числа от 11 до 20. число 20 состоит из двух пучков палочек - десятков.

При знакомстве ребенка с записью и чтением чисел от 11 до 20 хорошую помощь оказывает специальное наглядное пособие – абак:

Сначала счетные палочки по одной кладут в правый верхний кармашек абака, сопровождая этот процесс счетом. Получив десять палочек, их связывают в пучок (десяток) и перекладывают из правого кармашка в левый. В правый кармашек добавляют еще несколько палочек. Дойдя до числа пятнадцать, ребенку задают следующие вопросы:

• Сколько десятков в числе пятнадцать? (Один.) Обозначим это цифрой (внизу на абаке ставится разрезная карточка с цифрой 1).

• Сколько отдельных (т.е. не объединенных в десяток) единиц в числе пятнадцать? (Пять.) Обозначим это цифрой (под пятью палочками ставится цифра 5).

Аналогично ведется работа над записью и чтением остальных чисел второго десятка. При этом следует обратить внимание на объединение значения каждой цифры в записи числа: когда она обозначает количество единиц, а когда – десятков. Тем самым у ребенка формируется понимание позиционной записи двузначных чисел.

Сравнение двузначных чисел

При сравнении натуральных чисел в пределах 20 ребенок может уже самостоятельно использовать второй прием сравнения, основанный не на соотнесении соответствующих предметных множеств, а на взаимном расположении сравниваемых чисел в числовом ряду. Его рассуждения могут выглядеть так: «Шестнадцать больше четырнадцати, так как шестнадцать в ряду чисел находится правее, чем четырнадцать».

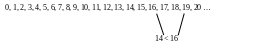
На этом этапе дети уже начинают при сравнении чисел использовать знаки «>, «<» и «=».

Предложив ребенку несколько заданий на сравнение однозначных чисел с двузначными, желательно так потом построить с ним обсуждение этой работы, чтобы он самостоятельно «открыл» следующую закономерность: любое однозначное число меньше любого двузначного числа.

Сложение и вычитание чисел вида 10 + 8, 18 – 10, 18 – 8

Уже при изучении нумерации чисел второго десятка первоклассники могут научиться выполнять простейшие случаи сложения и вычитания, основанные на разрядном составе двузначных чисел. Так, например, выполняя вычитание чисел вида 18 – 10, ребенок сопровождает его следующим комментарием: «Восемнадцать – это десять и восемь. Если из восемнадцати вычесть десять, то останется восемь». Аналогично проводятся рассуждения для случая 18 – 8. На первоклассном этапе решение таких примеров желательно сопровождать соответствующими предметными действиями, например, со счетными палочками.

Таким образом, заканчивая 1 класс, ребенок должен достаточно хорошо ориентироваться в следующих вопросах раздела «Нумерация целых неотрицательных чисел»: знать последовательность чисел в пределах 20 как в прямом, так и в обратном порядке, место каждого числа в натуральном ряду; уметь для каждого числа называть предыдущее и непосредственно следующее за ним число, продолжать счет как в прямом, так и в обратном порядке от любого заданного числа в этих пределах; понимать, как образуется каждое число путем прибавления единицы к предыдущему числу и вычитания единицы из последующего числа натурального ряда; читать, записывать и сравнивать любые числа в пределах 20, записывать результат сравнения с помощью знаков «>, «<» и «=»; до автоматизма знать состав чисел в пределах десяти, а также разрядный состав (из десятков и единиц) двузначных чисел второго десятка. В качестве опережения требований программы 1 класса можно с ребенком хорошо отработать знание состава всех чисел в пределах 18 из двух однозначных слагаемых (например, 14 = 7 + 7, 14 = 6 + 8, 14 = 5 + 9).

С целью контроля за усвоением этих вопросов ребенку можно предложить следующие задания.

Проверочные задания по темам

«Числа от 1 до 10» и «Числа от 11 до 20»

1. Посчитай от 1 до 20 сначала в прямом, а затем в обратном порядке.

2. Посчитай от 8 до 20 в прямом порядке, от 14 до 1 в обратном порядке.

3. Вставь пропущенные числа в ряду:

а) 1, 2, …, 4, 6, 7, …, …, 10, …, …, …, 14, …, …, …, 19 …

б) … 18, …, …, …, …, …, …, …, 10, …, 8, …, …, …, 4, …, …, 1.

4. Используя карточки с разрезными цифрами, попросите ребенка построить из них в «Кассе счетного материала» отрезок натурального ряда от 1 до 10. предложите ему отвернуться, а сами в это время переставьте между собой местами два каких-либо числа. Задача ребенка – найти перестановку и восстановить исходный ряд.

5. Поставьте нужные знаки >, < или =:

8 … 6; 11 … 17; 8 … 13;

4 … 9; 20 … 18; 14 … 5;

7 … 7; 13 … 10; 20 … 10;

0 … 5; 15 … 15; 9 … 11;

6. Замени каждое число суммой десятка и единиц по образцу:

12 = 10 + 2; 17 = … + …; 14 = … + …;

15 = … + …; 18 = … + …; 10 = … + …;

7. Заполни таблицы состава следующих чисел:

8
1
	6
3
	4
5
	2
7

9
8
	4
3
	5
7
	6
1
	2

14
9
	6
7
5

Нумерация от 21 до 100

Во 2 классе дети продолжают знакомство с двузначными числами в пределах от 21 до 100. эта тема изучается аналогично нумерации чисел от 11 до 20. вместе с тем, существует важная особенность, которая является причиной раздельного изучения этих двух числовых областей: если числа от 21 до 100 пишутся и читаются в одном и том же порядке (сначала десятки, потом - единицы, то во втором десятке читаются сначала единицы, а затем – десятки, в то время как запись числа осуществляется в обратном порядке. Ребенок сначала знакомится с разрядными числами («круглыми» десятками) – 20, 30, 40, 50, 60, 70, 80, 90, 100, - а затем со всеми остальными числами в пределах ста. При этом целесообразно использовать уже описанное выше наглядное пособие – абак:

При изучении чисел от 21 до 100 необходимо обратить особое внимание на чтение чисел 40 и 90, которое отличается от чтения остальных разрядных чисел.

Проверочные задания по теме

«Нумерация чисел от 21 до 100»

1. Назови числа по порядку: а) от 17 до 31; б) от 79 до 93; в) от 82 до 58.

2. Запиши числа по порядку: а) от 28 до 43; б) от 65 до 37.

3. Назови числа, которые предшествуют числам: 57, 81, 40.

4. Назови числа, которые следуют за числами: 34, 68, 70, 59, 99.

5. Назови «соседей числа: 42, 79, 50, 81.

6. Замени следующие числа суммой разрядных слагаемых: 35, 68, 70.

7. Сравни числа: 35 … 38; 57 … 27; 49 … 61; 90 … 53.

8. Сравни двузначные числа, в которых некоторые цифры заменены буквами (одинаковым цифрам соответствуют одинаковые буквы, знак 0 обозначает цифру «нуль»):

257 … 72; ж0 … ж7; ж5 … д5;

42 … 40; 3д … 4ж; жд …дж.

Тема: Методика изучения нумерации в концентре

«Тысяча»

План:

1. Цели обучения нумерации в пределах 1000.

2. Преемственность изучения нумерации чисел в концентре «Сотня» и «Тысяча» (сходство и различие).

3. Реализация задач темы на основе анализа фрагментов уроков.

- по ознакомлению с новой единицей «сотня».

- по ознакомлению с трехзначными числами.

4. Дидактические игры, способствующие закреплению различных вопросов нумерации.

Рекомендательная литература

1. Савина Л.П. Изучение чисел до 1000 // Начальная школа. – 1993. - №8. – С. 27-29.

В раздел, связанный с освоением нумерации трехзначных чисел, входит: изучение последовательности чисел в пределах 1000, их чтение и запись; знакомство с разрядом сотен, сотней как новой разрядной единицей; представление трехзначного числа в виде суммы разрядных слагаемых.

В целом методика изучения этой темы сходна с изучением нумерации двузначных чисел. Поэтому остановимся только на изучении записи трехзначных чисел. Для этого целесообразно использовать трехразрядный абак:

Для того, чтобы записать число 352, сначала построим его модель в верхнем ряду абака. В этой модели маленькие квадратики обозначают единицы, полоски – десятки (каждая полоска содержит 10 квадратиков), большие квадраты – сотни (каждый большой квадрат состоит из 100 маленьких или 10 полосок.) После этого проводится следующая беседа: «Сколько сотен в числе триста пятьдесят два?» (Три.) «Обозначим это цифрой» (в левый нижний кармашек вставляется карточка с цифрой три). «Сколько отдельных десятков?» (Пять.) (В средний кармашек вставляется цифра 5.) «Сколько в числе триста пятьдесят два отдельных единиц?» (Две.) (В правый нижний кармашек вставляется цифра 2.)

При изучении нумерации следует обратить внимание на формирование умения заменять любое трехзначное число суммой разрядных слагаемых:

583 = 500 + 80 + 3; 405 = 400 + 5; 620 = 600 + 20.

Более трудными являются случаи с числами, содержащими в записи нули. Так, иногда дети допускают следующие ошибки (во втором примере действие хотя и выполнено верно, но оно ошибочно представляет разрядный состав числа 600):

608 = 60 + 8 600 = 500 + 100.

Разрядный состав играет большую подготовительную роль в изучении арифметических действий над трехзначными числами.

Тема: Нумерация многозначных чисел

План:

1. Структура темы и задачи. Актуализация знаний по теме.

2. Знакомство со вторым классом – классом тысяч.

3. Изучение «круглых тысяч».

4. Изучение чисел, содержащих единицы 1-2 классов.

5. Виды упражнений на закрепление знаний по нумерации.

6. Обобщение знаний нумерации при ознакомлении с классами миллиона, миллиарда, триллиона.

Выполнить задания: подобрать упражнения с использованием следующих наглядных пособий;

а) перфокарта для проверки знаний по нумерации многозначных чисел;

б) папка для записи многозначных чисел;

средства наглядности к дидактическим играм.

Рекомендательная литература

1. Богданова И.Г. Методические приемы при изучении нумерации многозначных чисел // Начальная школа. – 1981. - №9. – С. 41-43.

2. Уткина Н.Г. Нумерация многозначных чисел. Изучение трудных тем по математике 1-3-х классах. – М.: Просвещение, 1982. – С. 89.

3. Бельтюкова Г.В. Изучение нумерации многозначных чисел // Начальная школа. – 1989. - №8. – С. 36-39.

В 4 классе программой предусмотрено знакомство с числами до 1 миллиона. Дети должны хорошо знать последовательность натуральных чисел в этих пределах, уметь читать и записывать многозначные числа, знать из разрядный состав. Основным средством при изучении нумерации многозначных чисел является таблица разрядов и классов:

Класс тысяч			Класс единиц
сотни тысяч	десятки тысяч	единицы тысяч	сотни	десятки	единицы
	5	9	0	7	8

Наибольшую трудность в данной теме представляет запись чисел, содержащих нули в середине, например: 59078, 830005 и т.д. Дети часто эти нули в записи пропускают. Чтобы предупредить данную ошибку, необходимо обратиться к таблице разрядов и классов. Например, нужно записать число «пятьдесят девять тысяч семьдесят восемь». Слово «тысяч» делит название числа на две части: все, что идет до этого слова следует записывать в классе тысяч, а что следует за ним – в классе единиц. В классе тысяч – пять десятков тысяч (пишем в этом разряде цифру пять) и девять единиц тысяч (пишем в этом разряде цифру 9.) В классе единиц – семь десятков и восемь единиц (пишем соответственно цифры 7 и 8). В классе единиц единицы разряда сотен отсутствуют – значит, на их месте пишем нуль. Таким образом, получается следующая запись – 59078 (см. таблицу).

Кроме таблицы разрядов и классов хорошую помощь в изучении нумерации могут оказать счеты.

МЕТОДИКА ИЗУЧЕНИЯ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

(8 часов)

Тема: Сложение и вычитание чисел в пределах 10

План:

1. Методика изучения конкретного смысла действий сложения и вычитания.

2. Характеристика знаний по нумерации, используемых учащимися при изучении данной темы.

3. Методика формирования вычислительного навыка.

4. Методика изучения табличных случаев.

5. Методика изучения приемов сложения и вычитания в пределах 10:

а) ±1;

б) ± 2, 3, 4;±

в) + 5, 6, 7, 8, 9;

г) - 5, 6, 7, 8, 9.

6. Работа с наглядными пособиями к работе над составом чисел.

7. Дидактические игры на закрепление теоретических навыков.

Рекомендательная литература

1. Моро М.И. Усилить внимание к формированию вычислительных навыков // Начальная школа. – 1984. - №7. – С. 34.

2. Истомина Н.Б., Шмырева Г.Г. Формирование навыков сложения и вычитания в пределах 10 // Начальная школа. – 1987. - №10. – С. 36-37.

3. Романова В.А. Работа над составом чисел // Начальная школа. – 1991. - №9. – С. 36-37.

4. Никитина Л.В. Как я учу шестилеток // Начальная школа. – 1987. - №9. – С. 48-50.

5. Попов В.К. Игра помогает учиться // Начальная школа. – 1987. - №2. – С. 39-40.

6. Моисеев О.И. Формирование приемов самоконтроля у первоклассников - шестилеток // Начальная школа. – 1987. - № 10. – С. 33-34.

Основные цели изучения сложения и вычитания в 1 классе

К концу 1 класса ребенок должен понимать конкретный смысл действий сложения и вычитания, до автоматизма знать таблицу сложения чисел в пределах десяти и соответствующие случаи вычитания. Однако достижение этих конечных результатов опирается на последовательное освоение конкретных вычислительных приемов, которые расположены в порядке возрастания степени трудности. В логике развертывания данной темы можно выделить следующие этапы: 1) прибавление к числу единицы и вычитание из числа единицы; 2) прибавление и вычитание чисел 2, 3, 4 (с использованием приема «по частям»); 3) изучение переместительного свойства сложения; 4) сложение чисел вида  + 5,  + 6,  + 7,  + 8,  + 9; 5) вычитание чисел вида  - 5,  - 6,  – 7,  - 8,  - 9; 6) составление таблиц сложения и вычитания в пределах десяти и их запоминание. В ходе данной темы дети учатся писать цифры. Необходимой предпосылкой для этого является хорошее развития у ребенка мелких мышц пальчиков, координации движений. Их развитию способствуют такие упражнения, как лепка, шитье, раскрашивание, штриховка и др. Опишем методику работы над этими вопросами более подробно.

Прибавление к числу единицы и вычитание

из числа единицы

В основе данного приема лежит хорошее владение ребенком счетом в пределах десяти в прямом и обратном порядке и знание соотношений между соседними числами. Этот материал был уже изучен в теме «Числа от 1 до 10». Поэтому прибавление к числу единицы и вычитание из числа единицы вводится с помощью следующих правил: а) чтобы прибавить к числу 1 нужно назвать следующее за ним число; б) чтобы вычесть из числа 1 нужно назвать предыдущее число. Эти случаи нужно обобщить (это удобно сделать в виде следующих таблиц) и запомнить:

1 + 1 = 2 6 + 1 = 7 2 + 1 = 3 7 + 1 = 8 3 + 1 = 4 8 + 1 = 9 4 + 1 = 5 9 + 1 = 10 5 + 1 = 6

2 – 1 = 1 7 – 1 = 6 3 – 1 =2 8 – 1 = 7 4 – 1 = 3 9 – 1 = 8 5 – 1 = 4 10 – 1 = 9 6 – 1 = 5

Сложение и вычитание в случаях вида   2,   3,   4

В основе решения всех примеров данного вида лежит прием, который называется «прибавление и вычитание по частям». Суть этого приема состоит в том, что второй компонент действия (числа 2, 3 или 4) дробится на более мелкие части и действия производятся последовательно с каждой частью. Покажем это на следующих примерах:

5 + 2 =		7 – 2 =		6 + 3 =		8 – 3 =		5 + 4 =		9 – 4 =
5+1+1		7-1-1		6+2+1		8–2-1		5+2+2		9–2–2

Приступая к изучению данного приема, необходимо повторить состав чисел 2, 3 и 4 из различных слагаемых. На начальном этапе освоения приема каждый пример желательно иллюстрировать наглядным материалом и сопровождать его выполнение предметными действиями (например, со счетными палочками). Приведем образец числовой записи, облегчающей восприятие приема сложения и вычитания «по частям»:

Сложение чисел вида  + 5,  + 6,  + 7,  + 8,  + 9

Этот случай в себя включает выражения, в которых второе слагаемое больше или равно пяти, например: 3 + 6; 2 + 7; 1 + 8. в этом случае первое слагаемое будет меньше пяти, т.к. действия осуществляются в пределах десяти. Это позволяет поменять слагаемые местами и использовать уже известный ребенку прием прибавления и вычитания «по частям»:

3 + 6 = ?

6 + 3 = 9

Таким образом, в основе сложения чисел вида  + 5,  + 6,  + 7,  + 8,  + 9 лежит переместительное свойство сложения, с которым необходимо предварительно познакомиться.

Вычитание чисел вида  - 5,  - 6,  - 7,  - 8,  - 9

Этот случай в себя включает выражения, в которых вычитаемое больше или равно пяти, например: 9 – 5; 8 – 6 и т.д. нахождение результатов в таких выражениях опирается на хорошее знание состава чисел первого десятка. Например, при вычислении значения выражения 9 – 6 = ребенок рассуждает следующим образом: «Девять – это шесть и три. Если из девяти вычтем шесть, то останется три». Эти рассуждения сопровождаются записью:

9 - 6 =

9 = 6 + 3

На первых этапах желательно, чтобы ребенок вслух комментировал решение таких примеров. Постепенно можно перейти к комментированию «про себя». При этом необходимость в записи «примера-помощника» (9 = 6 + 3) отпадает.

Проверочные задания по теме «Сложение и вычитание»

1. Найди значения выражений:

а) 6 + 4 = 3 – 2 = 3 + 6 =

9 – 7 = 2 + 8 = 10 – 8 =

3 + 5 = 8 – 5 = 6 + 1 =

6 – 3 = 3 + 7 = 3 – 3 =

10 – 4 = 9 + 1 = 6 – 2 =

2 + 8 = 9 – 3 = 5 + 4 =

1 – 0 = 4 + 5 = 6 – 0 =

1 + 0 = 8 – 5 = 4 + 4 =

2 + 3 = 9 – 6 = 7 + 2 =

10 – 9 = 4 + 0 = 9 – 0 =

8 + 0 = 7 – 6 = 4 + 4 =

9 – 4 = 9 + 1 = 7 – 6 =

б) 10 + 5 = 10 + 7 = 10+ 9 =

10 + 10 =

16 – 6 = 19 – 9 = 12 – 2 =

18 – 8 = 15 – 10 = 13 – 10 =

17 – 10 = 20 – 10 =

2. Вставь в окошко нужное число:

6 + 4 +ð = 13; 12 – 2 - ð = 6;

3 + ð + 7 = 17; 17 - ð - 8 = 2.

Тема: Сложение и вычитание чисел в пределах 20

План:

1. Задачи работы над темой.

2. Содержание подготовительного этапа.

3. Ознакомление с приемами сложения и вычитания с переходом через десяток.

4. Работа по осмыслению приемов сложения и вычитания и заучиванию таблиц наизусть. Методика формирования вычислительного навыка.

5. Дидактические игры к работе над темой.

6. Работа с индивидуальным наборным полотном с двумя рядами карманов по 10 штук

Рекомендательная литература

1. Моро М.И. Усилить внимание к формированию вычислительных навыков // Начальная школа. – 1984. - №7. – С. 34-36.

2. Уткина Н.Г. Изучение трудных тем по математике. – М.: Просвещение, 1982. – С. 10-18.

3. Петерсон Л.Г. Активация деятельности детей при изучении вычитания двузначных чисел с переходом через десяток // Начальная школа – 1997. - №6.

Сложение и вычитание с переходом через десяток

в пределах 20

Сложение чисел с переходом через десяток рассмотрим на примере случая 9 + 4. Для этого используется следующий прием: второе слагаемое (число 4) разбивается на две части (числа 1 и 3) так, чтобы первая часть (число 1) дополняло первое слагаемое (число 9) до целого десятка. Затем к целому десятку добавляется вторая часть (число 3) и получается ответ – число 13.

Чтобы наглядно представить этот процесс, используется двухрядное наборное полотно, каждый ряд которого состоит из 10 частей. Сначала на первый ряд выставляется 9 красных квадратов, а на второй ряд – 4 синих квадрата. Затем один синий квадрат переставляется в верхний ряд (т.к. там осталось место только для одного квадрата), а три квадрата остаются в нижнем ряду.

Числовая запись этого приема выглядит следующим образом:

Программой предусмотрено, что случаи сложения с переходом через десяток изучаются не все сразу, а постепенно, чтобы у ребенка была возможность не только понять сам прием, но и запомнить результаты каждого примера. В учебнике изучение сложения с переходом через десяток сгруппировано в несколько уроков так, что на каждом уроке рассматриваются преимущественно случаи сложения с одинаковым вторым слагаемым.

После изучения всех случаев сложения, они обобщаются и систематизируются в виде таблицы, которую нужно знать наизусть:

9 + 2	8 + 3	7 + 4	6 + 5	11
9 + 3	8 + 4	7 + 5	6 + 6	12
9 + 4	8 + 5	7 + 6		13
9 + 5	8 + 6	7 + 7		14
9 + 6	8 + 7			15
9 + 7	8 + 8			16
9 + 8				17
9 + 9				18

После сложения изучается вычитание с переходом через десяток. При этом, в отличие от сложения, рассматривается два приема вычитания:

1) Прием замены вычитаемого суммой двух частей, одна из которых равна количеству единиц уменьшаемого. Этот прием похож на рассмотренный выше прием сложения с переходом через десяток:

2) Прием. Основанный на соответствующих случаях сложения. Например, выполняя вычитание чисел вида 12 – 5, ребенок рассуждает следующим образом: «Двенадцать – это пять и семь. Поэтому, если из двенадцати вычтем пять, то останется семь». Запись в этом случае выглядит так:

12 – 5 = ?

12 = 5 + 7

Все случаи вычитания с переходом через десяток также должны быть постепенно выучены наизусть. Таким образом, в результате изучения этой темы ребенок должен наизусть знать таблицу сложения всех однозначных чисел (до 18 включительно) и на этой основе выполнять соответствующие случаи вычитания.

Тема: Методика изучения сложения и вычитания чисел от 21 до 100

План:

1. Задачи изучения темы.

2. Последовательность изучения устных приемов сложения и вычитания.

3. Методика использования свойств действий сложения и вычитания с теоретико-множественной точки зрения.

4. Методика формирования вычислительного навыка.

5. Различные подходы к изучению сложения и вычитания чисел 21-100.

Рекомендательная литература

1. Бантова М.А. Система формирования вычислительных навыков //Начальная школа. – 1993. - №11. – С. 38-44.

2. Бельтюкова Г.В. Методические ошибки при формировании у школьников вычислительных навыков // Начальная школа. - №8. – 20-27.

3. Белошистая А.В. Прием формирования устных вычислительных умений в пределах 100 // Начальная школа. – 1980. - №8. – С. 20-27.

4. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: ЛИНКА-ПРЕСС, 1997. – №2. - С. 36-39.

5. Моро М.И. Усилить внимание к формированию вычислительных навыков / Начальная школа. 1985. - №7. – С. 34-36.

6. Никулина А.М. Формирование у первоклассников навыков проверки арифметических действий //Начальная школа. – 1983. - №9. – С. 45-47.

7. Пиядин Н.С. Формирование вычислительных умений и навыков // Начальная школа. 1990. - №10. – С. 82-84.

8. Шилова Е.С. Занимательные задания для формирования вычислительных навыков // Начальная школа. – 1979. - №9. – С. 45-46.

9. Эрдниев П.М., Эрдниев Б.П. Теория и методика обучения математике в начальных классах. М.: Педагогика, 1988. – 208 с.

К концу учебного года ребенок должен уверенно складывать и вычитать числа в пределах ста (виды этих чисел перечислены ниже), знать правила, на которых основываются вычислительные приемы, и осознанно применять их в вычислениях. Арифметические действия осваиваются не над всеми сразу двузначными числами, а постепенно, начиная с самых простых случаев:

1) 30 + 20, 60 – 20, 80 + 20, 100 – 30;

2) правило замены соседних слагаемых их суммой;

3) 25 + 3, 3 + 25;

4) 50 + 23, 23 + 50;

5) 36 – 20, 36 – 2;

6) 26 + 4; 30 – 4;

7) 60 – 24;

8) 26 + 7;

9) 35 – 7;

10) Сложение и вычитание двузначных чисел в столбик:

а) 45 + 23; б) 57 – 26;

в) 37 + 48, 37 + 53, 87 + 13;

г) 50 – 24, 52 – 24.

Рассмотрим более подробно методику работы над перечисленными вычислительными приемами.

Сложение и вычитание разрядных чисел вида 30 + 20, 60 – 20 опирается на умение складывать и вычитать однозначные числа в пределах десяти. Рассуждения в данном случае выглядят следующим образом: «30 – это 3 десятка, а 20 – это 2 десятка. Если к 3 десяткам прибавим 2 десятка, то получим 5 десятков. 5 десятков – это 50 единиц, значит, 30 + 20 = 50».

На начальном этапе рассуждения можно сопровождать записью:

30 + 20 =

3д. + 2д. = 5д.

В дальнейшем запись можно сократить: 30 + 20 =50.

Если ребенок затрудняется с вычислением результата, то следует обратиться к предметным действиям с пучками счетных палочек:

Аналогично проводятся рассуждения при вычитании разрядных чисел вида 60 – 20. специально следует остановиться на случаях сложения и вычитания, в которых присутствует число 100: 80 + 20, 100 – 30. все остальные устные вычислительные приемы изучаются по одной и той же схеме. Поэтому мы ограничимся подробным рассмотрением методики изучения только одного приема: 23 + 50.

1) Подготовительный этап.

На подготовительном этапе отрабатываются следующие опорные знания: а) замена двузначного числа суммой разрядных слагаемых (23 = 20 + 3); б) сложение разрядных чисел (20 + 50 = 70); в) сложение разрядного числа с однозначным (70 + 3 = 73). Все эти операции являются составными частями вычислительного приема 23 + 50. поэтому, приступая к его изучению, необходимо добиться хорошего выполнения всех перечисленных операций.

2) Этап знакомства со свойством сложения, которое является теоретическим обоснованием данного вычислительного приема.

Для того, чтобы вычислительные приемы осваивались учащимися осознанно, программой предусмотрено знакомство со свойствами арифметических действий, выполняющих роль теоретических обоснований. В программе 1-3 роль теоретического обоснования выполняет правило прибавления числа к сумме. В программе 1-4 это правило используется в другой форме – в форме правила замены соседних слагаемых их суммой.

3) Этап знакомства с самим вычислительным приемом.

а) Выполнение предметных действий с использованием счетных палочек или полосок с кружочками:

б) Моделирование выполняемых предметных действий с помощью схемы. На схеме десяток можно обозначить треугольником с десятью точками-единицами. В дальнейшем точки можно не изображать, считая треугольник моделью десятка. В этом случае модель вычислительного приема 23 + 50 будет выглядеть следующим образом:

в) числовая запись вычислительного приема:

23 + 50 = (20+ + 3) + 50 = (20 + 50) + 3 = 70 + 3 = 73.

Так как некоторым детям бывает сложно в уме удержать последовательность выполняемых операций при решении данного примера, то в этом случае задать алгоритм можно в виде тройки опорных слов:

заменю …, получу …, удобнее …

ориентируясь на эти опорные слова, ребенок следующим образом комментирует выполнение данного примера: «Заменю число 23 суммой разрядных слагаемых 20 и 3; получу пример (20 + 3) + 50; удобнее к десяткам (20) прибавить десятки (50), получим семьдесят, семьдесят плюс три – получится семьдесят три».

4) В дальнейшем, на этапе формирования вычислительных навыков сложения и вычитания, отдельные операции постепенно начинают выполняться ребенком в умственном плане без подробной фиксации этих операций в виде моделей или числовых записей. Для формирования прочих вычислительных навыков в этот период нужно увеличить количество тренировочных упражнений, которые могут быть представлены в занимательной форме. Все остальные вычислительные приемы изучаются по этой же схеме, поэтому в данном методическом пособии они не рассматриваются.

Устные приемы сложения и вычитания в пределах 1000

Рассмотрим основные случаи устного сложения и вычитания в пределах 1000.

1) Сложение и вычитание чисел вида 500 + 400 и 700 – 200 основывается на сложении и вычитании однозначных чисел:

500 + 400 =		700 – 200 =
5 с. + 4 с. = 9 с.		7 с. – 2 с. = 5 с.

2) Сложение и вычитание чисел вида 340 + 200 и 870 – 600 сводится к сложению и вычитанию двузначных чисел:

340 + 200 =		870 – 600 =
34 д. + 20 д. = 54 д.		87 д. – 60 д. = 27 д.

Устные приемы умножения и деления в пределах 1000

В 3 классе изучаются простейшие случаи умножения и деления в пределах 1000.

1) Умножение и деление разрядных чисел сводится к умножению и делению однозначных чисел:

400 · 2 =		600 : 3 =
4 с. · 2 = 8 с.		6 с. : 3 = 2 с.

2) Случаи 60 · 7 и 540 : 6 опираются на табличное умножение и деление:

60 · 7 =		540 : 6 =
6 д. · 7 = 42 д.		54 д. : 6 = 9 д.

Тема: Письменные приемы сложения и вычитания

План:

1. Последовательность изучения темы по концентрам.

2. Переход от устных к письменным приемам сложения и вычитания двузначных чисел, формирование алгоритма письменного сложения и вычитания.

3. Особенности изучения вопроса в одном из альтернативных подходов (2, 123), (21, 168-202).

4. Предупреждение ошибок у учащихся при сложении и вычитании многозначных чисел.

Кроме устных приемов вычислений, во 2 классе ребенок должен осознанно и быстро складывать и вычитать любые двузначные числа «в столбик». Освоение этого осуществляется в следующей последовательности: 1) сложение двузначных чисел без перехода в другой разряд (57 - 26); 3) сложение двузначных чисел с переходом в другой разряд (37 + 48); 4) вычитание двузначных чисел с переходом в другой разряд (52 - 24).

Прием сложения в столбик опирается на правило прибавления суммы к сумме, которое в явном виде в начальных классах не изучается. Поэтому освоение данного приема можно начать в его иллюстрации на абаке с помощью счетных палочек (в верхнем ряду – число 45, в нижнем - число 23).

Перекладывая три отдельных счетных палочки из нижнего правого кармашка в верхний, а два пучка палочек – из нижнего левого кармашка в верхний, мы тем самым иллюстрируем способ прибавления десятков к десяткам, а единиц – к единицам. Эти предметные действия сопровождаются записью:

5 + 3 = 8; 40 + 20 = 60; 60 + 8 = 68.

Цель этой работы – помочь ребенку осознать данный вычислительный прием, предупредить его формальное выполнение. Только после этого формулируется алгоритм сложения в столбик:

+	45
	23

1. Пишу десятки под единицами, единицы под единицами.

2. Складываю единицы: 5 + 3 = 8.

3. Складываю десятки: 4 + 2 = 6.

4. Читаю ответ: 68.

Остальные случаи сложения и вычитания двузначных чисел в столбик рассматриваются аналогично. При их рассмотрении следует обратить внимание на наиболее сложные случаи, когда сложение и вычитание происходит с переходом в другой разряд: 37 + 48 и 52 – 24. при освоении этих приемов ребенок иногда забывает, что при сложении с переходом через десяток в разряд десятков нужно добавить еще одну единицу, а при вычитании с переходом через десяток из количества десятков уменьшаемого нужно вычесть одну единицу. Чтобы предупредить эту типичную ошибку, целесообразно использовать следующие приемы: при сложении над разрядом десятков дописывать цифру 1, а при вычитании над разрядом десятков ставить точку, обозначающую то, что один десяток из уменьшаемого заменили на десять единиц и добавили их к единицам уменьшаемого.

	1			•
+	37		–	52
	48			24
	85			28

Сложение и вычитание трехзначных чисел в столбик изучается на основе алгоритмов сложения и вычитания в столбик двузначных чисел. Отличие состоит только в том, что добавляется еще один шаг: «Складываю (вычитаю) сотни …». Все приемы фиксации в записи перехода в другой разряд остаются прежними.

Сложение и вычитание трехзначных чисел в столбик изучается на основе алгоритмов сложения и вычитания в столбик двузначных чисел. Отличие состоит только в том, что добавляется еще один шаг: «Складываю (вычитаю) сотни …». Все приемы фиксации в записи перехода в другой разряд остаются прежними.

Опираясь на алгоритмы письменного сложения и вычитания трехзначных чисел в столбик, можно легко перейти к сложению и вычитанию многозначных чисел. Обобщить этот вычислительный прием ребенок может и сам, без существенной помощи взрослого.

Следует особо выделить наиболее трудный случай вычитания чисел вида:

5. Вставь пропущенные цифры:

–	6005
	327

В этом примере дети часто вычитают 3 и 2 не из девяти, а из десяти. Чтобы предупредить эту ошибку, нужно подробно рассмотреть процесс дробления единиц более крупного разряда и распределения их между единицами более мелких разрядов: «Так как из 5 единиц нельзя вычесть 7 единиц, а единицы десятков и сотен в уменьшаемом отсутствуют, то из 6 тысяч берем 1 тысячу и дробим ее на 10 сотен. Из 10 сотен берем 1 сотню и заменяем ее на 10 десятков (остается 9 сотен, которые мы подписываем над разрядом сотен). Из 10 десятков берем 1 десяток и заменяем его на 10 единиц (цифру оставшихся 9 десятков подписываем над разрядом десятков). Десять единиц да пять единиц дают 15 единиц …». После этого процесс вычитания выполнить уже легко. Запись, таким образом, выглядит следующим образом:

	. 99
–	6005
	327

Выполнить задание:

1. На занятии изучите статьи по теме и выполните задание. Перечислите возможные ошибки учащихся при решении следующих примеров:

   +	121346		–	10004
   	3502			397

2. Самостоятельно выполните задания:

1. Вставьте пропущенные цифры:

   +	345?		–	64853
   	94?7			1?1??
   	1??39			?9?55

2. Вставьте в окошко число так, чтобы корень первого уравнения был равен корню второго уравнения:

х – 10003 = 513; х – (10003 + ?) = 499.

3. Пользуясь первым равенством, найдите значение второго равенства: 41835 – 2016 = 33819, 418835 – 2026 = ?

4. Сколько еще равенств можно составить используя равенство: 3612 – 837 = 2715.

5. Не выполняя действий сравните значение выражения с числом: 276 + 242 и 500.

6. Из чисел 699762, 8579, 92838, 167148 составьте и вычислите примеры на сложение и вычитание.

7. К заданиям 1-6 подберите и составьте еще по два примера.

8. Какие еще задания можно предложить для формирования у учащихся вычислительных навыков? Запишите их.

Рекомендательная литература

1. Волкова С.И., Моро М.И. Сложение и вычитание многозначных чисел // Начальная школа. – 1989. - №9. – С. 34-41.

2. Бельтюкова Г.В. Методические ошибки при формировании у школьников вычислительных навыков // Начальная школа. - 1980 - №8. – С. 20-27.

3. Уткина Н.Г. Изучение трудных тем по математике. – М.: Просвещение, 1982. – С. 10-18.

МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ ЗАДАЧ (12 часов)

Тема: Обучение решению простых задач на

сложение и вычитание

План:

1. Роль задач в начальном курсе математики (записать ответ на вопрос в тетрадь для лекций).

1. Обучение решению простых задач:

а) раскрывающих смысл действий сложения и вычитания;

б) на увеличение (уменьшение) числа на несколько единиц;

в) на разностное сравнение;

г) с неизвестным слагаемым;

д) с неизвестным уменьшаемым;

е) с неизвестным вычитаемым.

3. Анализ видав задач с теоретико-множественной точки зрения.

Рекомендательная литература

1. Гребенникова Н.Л. Ознакомление первоклассников с задачей // Начальная школа. 1990. - №10. – С. 34-37.

2. Истомина Н.Б. Первые шаги в формировании умения решать задачи //Начальная школа. – 1981. - №11. – С. 40-42.

3. Царева С.Е. Приемы первичного анализа задачи // Начальная школа. – 1985. - №9. – С. 46-49.

4. Шмырева Г.Г. Предупреждение ошибок в выборе арифметического действия при обучении решению задач // Начальная школа. – 1985. - №10. – С. 37-39.

В начальном курсе математики большую роль играют задачи. Они выполняют функцию не только самостоятельного объекта изучения, но и важного средства, с помощью которого младшие школьники осваивают математические понятия. В зависимости от количества действий, с помощью которых решается задача, различают задачи простые (в одно действие) и составные (в два и более действий) в начальных классах вводятся 25 видов только простых задач, каждый из которых имеет свои методические особенности. Поэтому решение обычно является «камнем преткновения» для младших школьников. В связи с этим, рассмотрим данный вопрос более подробно.

Что значит решить задачу? На этот вопрос отвечают, как правило, следующим образом: «Решить задачу – это значит найти правильный ответ». Но это не совсем так. решить задачу, это значит:

- разобраться в условии задачи, выделить входящие в нее величины, определить, какие из них известны, а какую надо найти;

- выяснить, как между собой эти величины связаны;

- на основе этого правильно выбрать арифметическое действие;

- записать соответствующий пример, вычислить его и записать ответ.

Как видим, решение задачи включает в себя следующие элементы: а) анализ условия задачи, выделение известных величин и той, которую надо найти; б) краткая запись условия задачи; в) разбор задачи, составление плана решения (в составных задачах); г) запись решения; д) проверка решения.

Виды задач в 1 классе

В 1 классе четырехлетней начальной школы дети знакомятся со следующими видами простых задач:

Вид задачи	Пример данного вида задачи
1. На нахождение суммы	У Саши было 6 тетрадей в клетку и 2 в линейку. Сколько всего тетрадей было у Саши?
2. На нахождение остатка	У Саши было 8 тетрадей. 2 тетради он сдал учителю. Сколько тетрадей у него осталось?
3. На увеличение числа на несколько единиц	У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради больше. Сколько всего тетрадей было у Саши?
4. На уменьшение числа на несколько единиц	У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради меньше. Сколько всего тетрадей было у Саши?

Задачи на нахождение суммы

Задачи на нахождение суммы раскрывают конкретный смысл действия сложения. Поэтому на подготовительном этапе работы над этим видом задачи необходимо постоянно оперировать с предметными множествами, делая упор на операцию объединения множеств. Приведем пример такой работы.

- Положи слева 5 красных кружочков, а справа – 3 синих кружочка. Придвинь синие кружочки к красным (при этом делается жест объединения синих кружочков с красными). Больше стало кружочков или меньше? (Больше.) Сколько всего стало кружочков? (8.) Каким действием это узнаем? (Сложением.)

В дальнейшем осуществляется переход предметных действий с кружочками к их моделям, которые вычерчиваются в тетради (размер кружочка – одна клеточка, интервал между ними тоже одна клеточка). В этом случае объединение множеств ребенок осуществляет мысленно и фиксирует это объединение на чертеже в виде стрелочки.

Для того, чтобы лучше разобраться в условии задачи, выделить входящие в нее величины, выполняется краткая запись условия, которая предшествует выбору арифметического действия и записи решения задачи. Для данного вида задач традиционной является следующая форма краткой записи условия (рассмотрим ее на примере приведенного выше текста задачи):

К. – 6 т.	?
Л. – 2 т.

Пояснение обозначений: К. – тетрадей в клетку, Л. – тетрадей в линейку.

Однако величины, входящие в условие задачи, и отношения между ними более наглядно отображаются в краткой записи условия, которая выполнена в виде следующих схем:

а) схема в форме полоски:

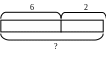
б) схема в форме отрезка:

Использование таких схем больше помогает детям правильно выбрать нужное арифметическое действие для решения задачи.

Решение задачи на данном этапе записывают следующим образом:

6 + 2 = 7 (т.)

Ответ: 8 тетрадей.

Задачи на нахождение остатка

Данный вид задачи раскрывает конкретный смысл действия вычитания. Методика работы с такими задачами похожа на предыдущий вид, только вместо операции объединения множеств используется операция удаления части множества. Традиционная форма краткой записи условии выглядит так:

Б. – 8 т.	Ост. - ?
С. – 2 т.

Пояснение обозначений: Б. – было, С. – сдал, Ост. - осталось.

Задачи на увеличение и уменьшение числа на несколько единиц

В основе правильного решения этих видов задач лежит понимание смысла отношений «больше на», «меньше на». Так, например, если тетрадей в клетку – 6, а в линейку на 2 больше, то это значит, что в линейку столько же, сколько в клетку, и еще 2. на схеме это отношение оформляется так:

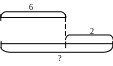
Проверочные задания по теме «Решение задач»

Реши задачи:

1. В одной тарелке 5 яблок, а в другой – 4 яблока. Сколько яблок в двух тарелках?

2. У Саши было 7 марок. 2 марки он подарил другу. Сколько марок осталось у Саши?

3. В одной вазе – 6 цветов, а в другой – на 2 больше. Сколько цветов во второй вазе?

4. В гараже было 8 легковых машин, а грузовых – на 3 меньше. Сколько грузовых машин было в гараже?

5. На столе лежат 5 ложек, а вилок на 2 больше, чем ложек. Сколько вилок лежат на столе?

6. Сшили 9 платьев, а блузок на 3 меньше, чем платьев. Сколько сшили блузок?

7. Антону 7 лет, а его сестре на 2 года меньше. Сколько лет сестре Антона?

8. К озеру идут 5 уток, а утят на 4 больше, чем уток. Сколько утят идут к озеру?

9. Феде 10 лет, а Петя моложе Феди на 3 года. Сколько лет Пете?

10. На берегу 7 пингвинов, а на льдине на 3 пингвина меньше. Сколько пингвинов на льдине?

Решение простых задач

Во 2 классе продолжают решать простые задачи. В дополнение к тем, которые были представлены в 1 классе, приведем еще несколько видов.

Вид задачи	Особенности работы над данным видом
На нахождение неизвестного слагаемого	Пример данного вида задачи: «В гараже было 5 грузовых и несколько легковых машин. Всего в гараже было 8 машин. Сколько легковых машин было в гараже?» Решение задач данного вида основывается на знании и умении применять следующее правило: «чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое». Однако опыт показывает, что дети не всегда осознанно используют это правило и решение данного вида задач часто усваивают формально. Для преодоления этой трудности могут оказать помощь следующие средства: 1) Построение моделей в виде отрезков. Построим модель для приведенной выше задачи: 2) Обращение к понятиям «часть» и «целое». В этом случае рассуждения ребенка по приведенной выше модели выглядят следующим образом: «Известно целое (8 м.) и часть (5 м.). чтобы найти часть, нужно из целого вычесть другую часть». 3) Одновременное решение задач на нахождение неизвестного слагаемого и задач на нахождение суммы, т.к. они являются взаимно обратными задачами.
На разностное сравнение	Различают два вида задач на разностное сравнение, которые отличаются друг от друга вопросом: 1) задачи с вопросом «на сколько больше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько легковых машин было больше, чем грузовых?); 2) задачи с вопросом «на сколько меньше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько грузовых машин в гараже было меньше, чем легковых?) Трудность состоит в том, что, несмотря на разные опорные слова в вопросах этих задач, обе они решаются действием вычитания. Дети же, ориентируясь на слово «больше», иногда для решения выбирают действие сложения. в установлении правильных отношений между величинами в задачах на разностное сравнение поможет «метод следов». Его суть состоит в следующем. На столе выкладывается в верхнем ряду 5 красных кружочков, а в нижнем ряду – 8 синих кружочков: затем кружочки убираются парами (по одному из каждого ряда) до тех пор, пока в верхнем ряду все кружочки не закончатся. В ходе этого процесса наглядно видно, почему задача решается действием вычитания:

Тема: Методика обучения решению простых задач на умножение и деление

План:

1. Самостоятельно изучить по учебникам (подобрать примеры) конкретный смысл операций умножения и деления с теоретико-множественной точки зрения и методика обучения решению простых задач следующих видов:

- задачи на нахождение суммы одинаковых слагаемых;

- задачи на деление по содержанию и делению на равные части;

- задачи на нахождение неизвестных компонентов действий умножения;

- задачи на увеличение в несколько раз;

- задачи на уменьшение в несколько раз;

- задачи на кратное сравнение.

2. По учебникам математики М2 [15] и М3 [16] классов сделать анализ задач вышеуказанных видов.

Рекомендательная литература

1. Царева С.Е. Проверка выбора действий при решении простых задач // Начальная школа. – 1981. - №9. – С. 35-37.

2. Царева С.Е. Приемы первичного анализа задачи //Начальная школа. – 1985. - №9. – С. 46-49.

3. Шмырева Г.Г. Предупреждение ошибок в выборе арифметического действия при обучении решению задач (нахождение неизвестных компонентов) // Начальная школа. – 1985. - №10. – С. 37-39.

Так как центральной темой 3 класса является умножение и деление, то новые виды простых задач связаны с этими действиями. Остановимся на методике решения трех видов простых задач: 1) на увеличение числа в несколько раз; 2) на уменьшение числа в несколько раз; 3) на кратное сравнение.

Вид задачи	Текст задачи	Краткая запись условия, разбор, запись решения задачи
На увеличение числа в несколько раз	В гараже находится 4 грузовых машины, а легковых – в 3 раза больше. Сколько легковых машин в гараже?	Краткая запись решения 1 вариант: Г. – 4 м. Л. - ?, в 3 раза больше. 2 вариант: В основе разбора задачи лежит понимание смысла отношения «в несколько раз больше»: если грузовых машин – 4, а легковых – в 3 раза больше, то это значит, что легковых машин – 3 раза по 4. этому отношению соответствует умножение. Запись решения 4 · 3 = 12 (м.).
На уменьшение числа в несколько раз	в гараже находится 12 грузовых машин, а легковых – в 3 раза меньше. Сколько легковых машин в гараже?	Краткая запись решения 1 вариант: Г. – 12. Л. - ?, в 3 раза больше. 2 вариант: Разбор задачи В основе разбора задачи лежит понимание смысла отношения «в несколько раз меньше. этому отношению соответствует действие деление. Запись решения 12 3 = 4 (м.).
На кратное сравнениие	В гараже находится 4 грузовых машины и 12 легковых. Во сколько раз легковых машин в гараже больше, чем грузовых?	Краткая запись решения 1 вариант: 2 вариант: Разбор задачи в основе разбора задачи лежит понимание смысла отношения «во сколько раз (больше) меньше? Этому отношению соответствует действие деление. Запись решения 12 4 = 3 (м.).

Тема: Простые и составные задачи

План:

1. Система простых задач начального курса математики (различные классификации: традиционный, подход П.М. Эрдниева, подход Н.Б. Истоминой).

1. Содержание упражнений подготовительного этапа при переходе от простых задач к составным.

2. Первое знакомство с составной задачей (ответ подготовить в виде плана-конспекта).

Рекомендательная литература

1. Свечников А.А. Решение математических задач в 1-3-х классах. – М., 1976. – С. 45-52.

1. Истомина Н.Б. Работа над составной задачей //Начальная школа. – 1988. - №2. – С. 44-49. (Подготовительный этап).

2. Уткина Н.Г. Составные задачи в 1-м классе // Изучение трудных тем по математике в 1-3-х классах. – М., 1982. – С. 45-52.

3. Гребенникова Н.Л. Опоры-перфокарты в обучении решению задач // Начальная школа. – 1992. - №7-8. – 38 с.

4. Смирнова С.И. Использование чертежа при решении простых задач // Начальная школа. – 1998. - №5. – С. 53-58.

Во 2 классе четырехлетней начальной школы впервые вводятся составные задачи (напомним, что составными называются задачи, которые решаются в два и более действий). Рассмотрим методику поэтапной работы с такими задачами:

Подготовительный этап. На этом этапе работа ведется с парами простых задач, таких, что ответ первой задачи является одним из данных чисел второй задачи. Приведем пример пары таких задач:

1) У Саши было 6 тетрадей в клетку и 2 тетради в линейку. Сколько всего тетрадей было у Саши?

2) У Саши было 8 тетрадей. 3 тетради он сдал учителю. Сколько тетрадей у него осталось?

В этой паре ответ первой задачи (8 тетрадей) является данным условием второй задачи.

На основе пары таких простых задач легко ввести составную задачу: У Саши было 6 тетрадей в клетку и 2 тетради в линейку. 3 тетради он сдал учителю. Сколько тетрадей у него осталось?

Основная трудность в решении таких задач состоит в том, что ребенок Перове действие выполняет в уме, а общее решение записывает так:

8 – 3 = 5 (т.)

На вопрос: «Откуда взялось число 8? Ведь его в условии задачи не было», чаще всего дети дают такой ответ «Но ведь 6 и 2 будет 8».

Решение пар простых задач позволяет предупредить эту ошибку и помочь детям осознать тот факт, что одним действием такую задачу решить нельзя.

Этап знакомства с составной задачей. Дети знакомятся с составной задачей на примере двух вариантов задач:

1) составной задачи, в которой первое действие является простой задачей на уменьшение числа на несколько единиц, а второе – простой задачей на нахождение суммы («В первой тарелке 5 груш, а во второй на 2 груши меньше. Сколько груш в двух тарелках?»);

2) составной задачи, в которой первое действие является простой задачей на нахождение суммы, а второе – простой задачей на нахождение остатка («Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку. Сколько флажков осталось?»). на примере этих задач рассмотрим методические особенности работы с ними.

Процесс работы над задачей состоит из следующих основных этапов:

1) Краткая запись условия задачи, которая помогает лучше разобраться в ее содержании.

2) Разбор задачи, в ходе которого выявляются отношения между данными и искомой величиной, осуществляется выбор арифметического действия.

3) Запись решения задачи и полученного ответа.

Для первого варианта составной задачи эти этапы будут выглядеть следующим образом.

Текст задачи

«В первой тарелке 5 груш, а во второй на 2 груши меньше. Сколько груш в двух тарелках?»

Краткая запись условия

Разбор задачи

- Что известно в задаче? (В первой тарелке 5 груш, а во второй на 2 груши меньше.)

- Какой главный вопрос в задаче? (Сколько груш в двух тарелках?)

- Можем ли мы сразу ответить на этот вопрос? (Нет.)

- Что для этого нужно знать (Сколько груш в каждой тарелке.)

- Сколько груш в первой тарелке? (5.)

- А что сказано про вторую? (В ней на 2 груши меньше.)

- Как узнать, сколько груш во второй тарелке? (Нужно из 5 вычесть 2.)

- Как потом узнать, сколько груш в двух тарелках? (Нужно к тому, что получится в первом действии, прибавить 5.)

- Верно. Итак, сколько действий в этой задаче? (Два.)

- Какое первое действие? (Из 5 вычтем 2.)

- Что мы узнаем, выполнив это действие? (Сколько груш во второй тарелке.)

- Что будем делать во втором действии? (К результату первого действия прибавим 5.)

- Что узнаем, выполнив это действие? (Сколько груш в двух тарелках.)

Запись решения задачи

(с пояснением)

1) 5 – 2 = 3 (г.) – было во 2 тарелке.

2) 5 + 3 = 8 (г.) – всего в двух тарелках.

Ответ: 8 груш.

Приведем пример реализации данных этапов для второго варианта составной задачи.

Текст задачи

«Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку. Сколько флажков осталось?»

Краткая запись условия

Вырезали – 6 ф. и 4 ф.

Повесили – 3 ф.

Осталось - ?

Разбор задачи

(синтетический способ)

- Что известно в задаче? (Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку.)

- Какой главный вопрос в задаче? (Сколько флажков осталось?)

- Зная, что вырезали 6 красных флажков и 4 синих, что мы можем узнать? (Сколько всего флажков вырезали.)

- Каким действием это узнаем? (Сложением.)

- Зная, сколько флажков вырезали, и что 3 флажка их них повесили на елку, что мы можем найти? (Сколько флажков осталось.)

- Каким действием найдем? (Вычитанием.)

Запись решения задачи

(составлением выражения)

(6 + 4) – 3 = 7 (ф.)

Ответ: 2 ф.

Как видим, на примере, двух вариантов составных задач представлены основные способы краткой записи условия, разбора и записи решения, которые используются во 2 классе. Рассмотрим их более подробно.

Краткая запись условия задачи начинает вводиться постепенно. Сначала для этого используются начальные буквы опорных слов, а затем и сами опорные слова: «Было», «подарил», «продали», «улетело», «осталось» и т.д. При работе над вторым вариантом задачи использована такая краткая запись условия. Однако она не всегда помогает отразить реальные отношения между данными и искомыми величинами в задаче. Поэтому при решении как простых, так и составных задач мы рекомендуем использовать краткую запись в виде схем, чертежей, отрезков. Пример такой краткой записи условия приведен в первой задаче.

В начальной школе используются два основных способа рассуждений при разборе задачи: аналитический и синтетический. Аналитический способ более подробный, он начинается с главного вопроса задачи и постепенно восходит к величинам, данным в условии. Он используется, как правило, при освоении нового вида задачи. При синтетическом способе рассуждений мысль движется в обратном порядке: от условия задачи к главному вопросу. Этот способ является менее развернутым и пользуется, как правило, при разборе уже знакомых задач.

После разбора задачи переходят к записи ее решения. В настоящее время в начальной школе наиболее распространенной является запись решения по действиям с кратким пояснением результата действия. Этот способ показан в первой задаче. Освоив запись решения по действиям, можно переходить к записи решения способом составления выражения. В выражении выполняются те же действия, но они представлены в свернутом виде, поэтому данный способ требует более высокого уровня умения решать задачи.

Тема: Обучение решению задач с

пропорциональными величинами

План:

1. Упражнения в учебнике, приводящие к понятиям «прямая и обратная зависимость».

1. Формирование представлений о прямопропорциональной и обратнопропорциональной зависимости.

2. Простые задачи с тройкой пропорциональных величин и особенности работы с ними.

3. Составные задачи с пропорциональными величинами:

а) составные задачи, содержащие в качестве одной из простых задачи с тройкой пропорциональных величин;

б) задачи на нахождение четвертого пропорционального;

в) задачи на пропорциональное деление;

г) задачи на нахождение неизвестного по двум разностям.

Рекомендательная литература

1. Скаткин Л.Н., Жигалкина Т.К. Обучение решению задач с пропорциональными величинами. – М.: Просвещение, 1979. – 32 с.

1. Гребенникова Н.Л. Решение задач на зависимость величин различными способами // Начальная школа. – 1999. - №2. – С. 45-49.

2. Казько Е.С. Работа с текстом задачи с пропорциональными величинами // Начальная школа. – 1998. - №5. – С. 70-74.

В начальных классах дети знакомятся с тройками пропорциональных величин: цена, количество, стоимость; скорость, время, расстояние; масса одного предмета, количество предметов, общая масса и т.д. С этими величинами можно особо выделить 3 вида составных задач: на нахождение четвертого пропорционального; на пропорциональное деление; на нахождение неизвестного по двум разностям. Первый из этих видов вводится в 3 классе, а второй и третий – в 4 классе. рассмотрим особенности работы над задачами на нахождение четвертого пропорционального с величинами: цена, количество, стоимость.

На подготовительном этапе в ходе решения простых задач отрабатываются правила нахождения одной из величин по двум другим, пропорциональным ей: например, как найти цену, зная стоимость и количество. После этого можно перейти к решению составных задач.

Текст задачи

За 5 метров ткани заплатили 40 рублей. Сколько стоят 7 метров такой же ткани?

Краткая запись условия

Запись условия задач с пропорциональными величинами оформляется в виде таблицы:

Цена	Количество	Стоимость
Одинаковая	5 м 7 м	40 р. ?

Разбор

На начальном этапе разбор таких задач осуществляется аналитическим способом:

- Что известно в задаче? (Что за 5 метров ткани заплатили 40 рублей.)

- Что еще дано в условии задачи? (7 метров такой же ткани.)

- Какой главный вопрос задачи? (Сколько стоят 7 метров такой же ткани?)

- Можем ли мы сразу ответить на главный вопрос задачи? (Нет.)

- Что для этого нужно знать? (Для того, чтобы найти стоимость, нужно знать цену и количество.)

- Количество известно, а что сказано про цену? (Что она одинаковая.)

- Как же найти цену по стоимости и количеству? (Нужно стоимость (40 р.) разделить на количество (5 м.))

- Найдя цену, как узнаем стоимость 7 метров ткани? (Цену умножим на количество метров.)

Запись решения

1 способ – по действиям с пояснением:

1) 40 : 5 = 8 (р.) – стоит 1 м ткани.

2) 8 · 7 = 56 (р.) – стоят 7 м ткани.

Ответ: 56 рублей

2 способ – составлением выражения:

40 : 5 · 7 = 56 (р.)

Ответ: 56 рублей

В дальнейшем от аналитического способа разбора можно переходить к синтетическому, а краткую запись условия можно сделать более компактной:

5 м – 40 р.

7 м - ?

Наиболее сложными задачами, которые изучаются в з классе, являются задачи, связанные с пропорциональными величинами. Рассмотрим решение этих задач на примере задачи на нахождение неизвестных по двум разностям и задачи на пропорциональное деление.

Вид задачи	На пропорциональное деление
Условие	В магазин привезли 6 ящиков картофеля и 4 таких же ящика свеклы. Всего в магазин привезли 120 кг овощей. Сколько килограммов картофеля и сколько килограммов свеклы привезли в магазин?
Краткая запись условия
Разбор задачи	Аналитический способ разбора: Что известно в задаче? Что нужно узнать в задаче? Можем ли мы сразу ответить, сколько килограммов картофеля привезли в магазин? (Нет.) Что для этого нужно знать? (Массу одного ящика и количество ящиков.) Количество ящиков известно, а как можно найти массу одного ящика? (Общую массу разделить на общее количество ящиков.) Как приведем общее количество ящиков? (К 6 прибавим 4.) Узнав массу одного ящика, как найдем массу всего картофеля? (Массу одного ящика умножим на количество ящиков с картофелем.) Как узнать массу всей свеклы? (Массу одного ящика умножим на количество ящиков со свеклой.) Как можно другим способом узнать массу всей свеклы? (из общей массы вычесть массу картофеля.)
Запись решения	Запись решения по действиям с пояснением: 6 + 4 = 10 (ящ.) – привезли всего. 120 : 10 = 12 (кг) – масса одного ящика. 12 · 6 = 72 (кг) – привезли картофеля. 12 · 4 = 48 (кг) – привезли свеклы. Ответ: 72 кг и 48 кг.
Вид задачи	На нахождение неизвестных по двум разностям
Условие	В магазин привезли 6 ящиков картофеля и 4 таких же ящика свеклы, причем картофеля привезли на 24 кг больше, чем свеклы. Сколько килограммов картофеля и сколько килограммов свеклы привезли в магазин?
Краткая запись условия	Из этой наглядной записи хорошо видно, что 24 кг картофеля находятся в 2 ящиках.
Разбор задачи	Синтетический способ: Что известно в задаче? Что нужно узнать в задаче? Почему картофеля оказалось в магазине на 24 кг больше (Потому, что ящиков с картофелем было больше.) На сколько ящиков больше? (на 2.) Какой вывод из этого можно сделать? (Что 24 кг картофеля находится в 2 ящиках.) Зная это, как найти массу одного ящика с картофелем? (Нужно 24 кг разделить на 2.) Как теперь найти массу картофеля и массу свеклы? (Массу одного ящика умножить на количество ящиков.)
Запись решения	Запись решения с предварительной постановкой вопросов: На сколько ящиков картофеля привезли больше, чем свеклы? 6 – 4 = 2 (ящ.) Какова масса одного ящика с овощами? 24 : 2 = 12 (кг) Сколько килограммов картофеля привезли в магазин? 12 · 6 = 72 (кг) Сколько килограммов картофеля привезли в магазин? 12 · 4 = 48 (кг) Ответ: 72 кг картофеля и 48 кг свеклы.

Тема: Методика работы над задачами на движение

План:

1. Подготовительные упражнения к теме (на нахождение расстояния, промежутка времени, скорости).

1. Простые задачи с тройкой пропорциональных величин: скорость – время - расстояние, последовательность работы над вопросом.

2. Задачи на движение:

а) подготовительные составные задачи на движение одного или двух тел;

б) задачи на движение в противоположных направлениях и новые понятия, возникающие в связи с их решением (скорость сближения – при встречном движении и скорость удаления – при движении друг от друга);

в) движение в одном направлении.

Рекомендательная литература

1. Лысенкова С.Н. Когда легко учиться. – М., 1985.

1. Рудницкая В.Н. Формирование у школьников понятия «скорость» // Начальная школа. – 1993. - №1. – С. 40-43.

2. Холомкина А.И. Решение задач на движение // Начальная школа. – 1983. - №3. – С. 46-49.

Тема: Общий порядок работы над задачей

Выполнить задания:

1. Описание общего порядка работы над задачей.

2. Оформить решение задачи в тетради ученика.

3. Анализ традиционного и одного из альтернативных подходов при работе над задачей.

Рекомендательная литература

1. Свечников А.А. Решение математических задач в 1-3 классах. – М., 1976.

2. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: ЛИНКА-ПРЕСС, 1997. – 288 с.

3. Царева С.Е. Обучение решению задач // Начальная школа. – 1997. - №11. – С. 93-98.

МЕТОДИКА ИЗУЧЕНИЯ УМНОЖЕНИЯ И ДЕЛЕНИЯ

(12 часов)

Тема: Табличное умножение и деление

План:

1. Подготовительный этап к изучению табличного умножения и деления:

- упражнения на нахождение суммы одинаковых слагаемых;

- ознакомление с конкретным смыслом умножения и терминологией;

- изучение перестановки множителей и применение этого правила в вычислениях;

- таблица умножения с числом 2;

- ознакомление с конкретным смыслом действия деления по содержанию, деление на равные части и с терминологией;

- обобщение двух видов деления;

- изучение взаимосвязи между результатом и компонентом действий умножения и деления.

2. Методика изучения табличных случаев умножения и деления.

3. Альтернативные подходы к изучению умножения и деления.

Рекомендательная литература

1. Вершинин Н.Я. Игры при изучении табличных случаев деления и умножения // Начальная школа. – 1987. - №2. – С. 38-39.

2. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: ЛИНКА-ПРЕСС, 1997. – 288 с.

3. Методическая копилка // Начальная школа. – 1998. - №2.

4. Никулина А.Д. Изучение табличного умножения и деления // Начальная школа. – 1987. - №10. – С. 42.

5. Пиядин Н.С. Умножение и деление в новой дидактической системе обучения // Начальная школа. – 1997. - №7. – С. 26-34.

6. Серебрянникова Л.С. Я учу таблицу // Начальная школа. – 1997. - №5. – С. 67-72.

7. Туркина В.М. Работа по составлению таблицы умножения // Начальная школа. – 1987. – 1998. - №5. – С. 58.

8. Унгру Ю.П. Пособие для изучения таблиц сложения и умножения // Начальная школа. – 1987. - №5. – С. 42-43.

9. Урок в системе развивающего обучения: из опыта работы / под ред. Дусавицкого А.К. – Харьков, 1998. – 61 с.

10. Уткина Н.В. Таблица умножения // Изучение трудных тем по математике в 1-3 классах / Сост. Н.Г.Уткина. – М.: Просвещение, 1982.

Новые арифметические действия умножения и деления вводятся в четвертой четверти 2 класса. Основная задача в этот период состоит в том, чтобы ребенок понял конкретный смысл этих действий.

Так как умножение является частным случаем сложения, то данную работу можно провести следующим образом. Предлагаем ребенку 7-8 различных сумм, среди которых 2-3 состоят одинаковых слагаемых:

2 + 3 + 4 = 5 + 5 = 3 + 3 + 3 + 3 =

3 + 3 + 7 = 9 + 4 = 7 + 5 + 3 =

Сравнивая между собой эти суммы, выделяем те из них, которые состоят из одинаковых слагаемых. После этого можно объяснить, что в математике такие суммы записываются более кратко: сначала пишется число, которое складывается, затем пишется число, равное количеству слагаемых, и между ними ставится точка, обозначающая новое действие – умножение:

5 + 5 = 5 · 2 (но не 2 · 5);

3 + 3 + 3 + 3 = 3 · 4;

7 + 7 + 7 = 7 · 3.

Убедившись, что ребенок понял смысл умножения, ему можно предложить потренироваться в замене сложения умножением и наоборот.

Так же как и у других действий, у умножения каждое число имеет свое «имя»:

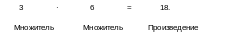
После усвоения конкретного смысла умножения можно перейти к следующему действию – делению. Различают два вида деления: 1) деление по содержанию; 2) деление на равные части. Приведем примеры этих видов деления:

Деление по содержанию	6 карандашей разложили в коробки, по 2 карандаша в каждую. Сколько потребовалось коробок?
Деление на равные части	6 карандашей разложили поровну в 3 коробки. Сколько карандашей в каждой коробке?

Знакомство с действием деления лучше начинать с деления по содержанию на основе практических действий с предметами усваивается конкретный смысл деления, показывается его запись. После этого можно перейти к делению на равные части.

Правила нахождения неизвестных компонентов умножения и

деления

Правило нахождения неизвестных множителя, делимого и делителя изучаются по одной и той же схеме в начале 3 класса: 1) на основе практической задачи составляется пример на умножение или деление; 2) к нему подбираются два взаимно-обратных примера; 3) на основе соотнесения названий компонентов в этих взаимно-обратных примерах выводятся соответствующие правила.

Рассмотрим это на примере правила нахождения неизвестного множителя.

1) 4 · 3 = 12;

2) 12 : 4 = 3;

3) 12 : 3 = 4.

Так как 3 и 4 – это множители, а 12 – произведение, то из 2) и 3) легко выводится правило:

Если произведение двух чисел разделить на один из множителей, то получится другой множитель.

Аналогично выводятся правила нахождения неизвестного делимого и делителя.

Табличное умножение и деление

Табличное умножение и деление является центральной темой 3 класса. От того, насколько у ребенка будут успешно сформированы навыки в пределах табличных случаев, во многом зависит процесс дальнейшего освоения арифметических действий. Табличное умножение и деление к концу 3 класса должно быть отработано до автоматизма. Для сокращения количества случаев табличного умножения и деления предварительно изучается переместительное свойство умножения. Это позволяет после знакомства, например, со случаем 3 · 8 не рассматривать отдельно случай 8 · 3, т.к. 3 · 8 = 8 · 3.

Изучение всех случаев табличного умножения и деления от 2 до 9 равномерно рассредоточено в течение длительного времени и осуществляется по одному и тому же плану. Поэтому мы ограничимся рассмотрением этой темы на примере числа 4.

В подготовительный период нужно хорошо отработать следующие вопросы: понимание конкретного смысла действий умножения и деления; название компонентов и результатов этих действий и правило нахождения неизвестного множителя; переместительное свойство умножения; счет «четверками».

Эти опорные знания используются при составлении следующих четырех столбиков примеров:

4 · 4 =				16 : 4 =
4 · 5 =		5 · 4 =		20 : 4 =		20 : 5 =
4 · 6 =		6 · 4 =		24 : 4 =		24 : 6 =
4 · 7 =		7 · 4 =		28 : 4 =		28 : 7 =
4 · 8 =		8 · 4 =		32 : 4 =		32 : 8 =
4 · 9 =		9 · 4 =		36 : 4 =		36 : 9 =

Результаты первого столбика находятся на основе перехода от умножения к сложению:

4 · 4 = 4 + 4 + 4 + 4 = 16;

4 · 5 = 4 · 4 + 4 = 16 + 4 = 20;

………..............

4 · 9 = 4 · 8 + 4 = 32 + 4 = 36.

Результаты второго столбика составляются на основе первого столбика с использованием переместительного свойства умножения («так как 4· 7 = 28, то и 7 · 4 = 28»).

Результаты третьего и четвертого столбиков также составляются на основе первого столбика с использованием правила нахождения неизвестного множителя: «Если произведение 20 разделить на первый множитель 4, то получится второй множитель - 5». Только разобравшись со способами нахождения результата для каждого примера, можно переходить к заучиванию таблицы умножения и деления наизусть.

Тема: Внетабличное умножение и деление

План:

1. Общая характеристика темы.

2. Теоретическая основа изучения внетабличного умножения:

а) правило умножения суммы на число;

б) умножение десятков на число;

в) формирование вычислительного приема;

3. Теоретическая основа изучения внетабличного деления:

а) правило деления суммы на число;

б) деление десятков на число;

в) формирование вычислительного навыка.

4. Деление двузначного числа на двузначное.

5. Последовательность изучения деления с остатком.

6. Частные и особые случаи умножения и деления с 0 и 1.

7. Анализ методических статей по теме.

Рекомендательная литература

1. Уткина Н.Г. Изучение трудных тем по математике. – С. 71-88.

2. Вапняр Н.Ф. Изучение темы «Деление с остатком» // Начальная школа. – 1981. - №1. – С. 36-38.

3. Степанова С.В. Случаи умножения и деления с числами 0 и 1 // Начальная школа. – 1984. - №10. – С. 42-45.

4. Ивашова О.А. К вопросу о рационализации вычислений // Начальная школа. – 1998. – №2. – С. 86-90.

Внетабличное умножение и деление изучается в следующей последовательности:

1. Умножение и деление разрядных чисел вида 20 · 3; 3 · 20; 60 : 2; 80 :20;

2. Правило умножения суммы на число;

3. Умножение двузначного числа на однозначное;

4. Правило деления суммы на число;

5. Деление двузначного числа на однозначное;

6. Деление двузначного числа на двузначное;

7. Умножение и деление разрядных чисел.

Умножение и деление разрядных чисел сводится к умножению и делению однозначных чисел:

20 · 4 =		60 : 2 =		2 · 30 =
2 д. · 4 = 8 д.		6 д. : 2 = 3 д.		30 · 2 = 60

Правило умножения суммы на число

Правило умножения суммы на число выполняет роль теоретического обоснования умножения двузначного числа на однозначное, а правило деления суммы на число - деления двузначного числа на однозначное. Методику изучения правил рассмотрим на примере правила умножения суммы на число.

При изучении этого правила ребенок должен понять, что суммы на число можно умножить двумя способами: 1) вычислить сумму и результат умножить на число; 2) каждое слагаемое умножить на число и полученные результаты сложить. Для этого целесообразно использовать следующую наглядность:

На этом рисунке изображены два ряда геометрических фигур, по 4 квадрата и 3 кружочка в каждом ряду. Нужно посчитать, сколько всего геометрических фигур изображено на рисунке. Это можно сделать двумя способами:

1) сложить количество кружочков и квадратов в одном ряду ( 4 + 3) и полученный результат умножить на 2:

(4 + 3) · 2 = 7 · 2 = 14;

2) отдельно посчитать квадраты и отдельно – кружочки, а затем полученные результаты сложить:

(4 + 3) · 2 = 4 · 2 + 3 · 2 = 8 + 6 = 14.

Умножение двузначного числа на однозначное

Освоение приема умножения двузначного числа на однозначное осуществляется в следующей последовательности:

1) Выполнение приема на уровне предметных действий. Например, при решении примера 23 · 4 можно четыре раза взять по два пучка палочек (число 20) и по три отдельных палочки.

2) Моделирование предметных действий в виде схемы:

23 · 4 = 92.

1. Числовая запись вычислительного приема:

23 · 4 = (20 + 3) · 4 = 20 · 4 + 3 · 4 = 80 + 12 = 92.

При выполнении данного вычислительного приема требуются следующие опорные знания: а) замена двузначного числа суммой разрядных слагаемых (23 = 20 + 3); б) умножение разрядного числа на однозначное (20 · 4); в) табличное умножение (3 · 4); г) сложение двузначных чисел (80 + 12). Все эти опорные знания необходимо включить в подготовительный этап, предшествующий освоению вычислительного приема.

Аналогичным образом изучается деление двузначного числа на однозначное.

Деление двузначного числа на двузначное

Деление двузначного числа на двузначное производится методом подбора. например, решая пример 72 : 12, ребенок рассуждает следующим образом: «Подберем число, которое при умножении на 12 даст число 72. это будет число 6. значит, 72 12 = 6».

Деление с остатком

Основное назначение данной темы – подготовить ребенка к выполнению деления многозначных чисел в столбик.

На первом этапе следует обратить его внимание на то, что не всегда одно число делится на другое. В этом случае говорят о делении с остатком. Запись деления с остатком выглядит так:

17 : 3 = 5 (ост. 2).

На следующем этапе осуществляется знакомство с основным свойством деления с остатком: остаток от деления всегда меньше делителя. Это можно сделать следующим образом. Выберем несколько чисел, например: 12, 13, 14, 15, 16, 17. Будем поочередно каждое из этих чисел делить на числа 2. 3, 4, фиксируя получившиеся при этом остатки. Это удобно сделать в виде таблицы:

Делитель	Остаток
2	0, 1
3	0, 1, 2
4	0, 1, 2, 3

Сравнивая остатки с делителем, ребенок может сам сделать вывод о том, что остаток всегда меньше делителя. В противном случае цифру частного можно увеличить на единицу.

Особые случаи умножения и деления

Умножение единицы на число:

1 · 4 = 4.

Основание: 1 · 4 = 1 + 1 + 1 + 1 = 4.

Умножение числа на единицу:

3 · 1 = 3.

Обоснование: этот случай нельзя обосновать путем перехода к сложению («взять число 3 слагаемым один раз»), т.к. сумм с одним слагаемым не существует. Поэтому данный случай является исключением и не обосновывается, а вводится в виде правила: «При умножении любого числа на 1 получается то же самое число».

Деление на единицу:

5 : 1 = 5.

Обоснование проводится путем перехода от деления к умножению: «Какое число нужно умножить на 1, чтобы получить 5? Число 5. Значит, 5 разделить на 1 будет 5».

Умножение и деление с числом 10:

10 · 4 = 40; 4 · 10 = 40; 40 : 4 = 10; 40 : 10 = 4.

Обоснование. Так как 10 = 1 дес., то данные случаи сводятся к умножению и делению с числом 1.

Умножение нуля на число:

0 4 = 0.

Обоснование: 0 · 4 = 0 + 0 + 0 + 0 = 0.

Умножение числа на нуль:

3 · 0 = 0.

Обоснование: этот случай также нельзя обосновать путем перехода к сложению («взять число 3 слагаемым нуль раз»), т.к. сумм с нулем слагаемых не существует. поэтому данный случай также является исключением и не обосновывается, а вводится в виде правила: «При умножении любого числа на нуль получается нуль».

Деление числа на нуль:

5 : 0 = ?

Обоснование проводится также путем перехода от деления к умножению: «Какое число нужно умножить на 0, чтобы получить 5? Такого числа не существует. Значит, на нуль делить нельзя!»

Тема: Умножение и деление на однозначное число

План:

1. Умножение и деление трехзначного числа на однозначное число.

2. Умножение и деление многозначного числа на однозначное число:

- повторение основной теории (смысл умножения и деления, свойства действий связь компонентов и результата действий, частные и особые случаи);

- устные и письменные вычисления;

- алгоритм письменного умножения и деления.

3. Формирование навыков письменного умножения и деления при рассмотрении частных случаев:

- умножение и деление числа с нулем в конце и в середине записи числа;

- определение первого неполного делимого при делении на однозначное число;

- определение количества цифр в частном и пробной цифры в частном;

- случай, когда хотя бы одна из цифр частного – нуль.

4. Анализ журнальных статей по теме.

Рекомендательная литература

1. Шандрук Т.Н. Случай деления с нулем в частном // Начальная школа. – 1982. - №3. – С. 56.

2. Бельтюкова Г.В. Приемы проверки пробной цифры частного // Начальная школа. – 1978. - №2. – С. 38-42.

Умножение на однозначное число

а) При подготовке к изучению этого приема необходимо повторить правило умножения суммы на число, которое обосновывает данный вычислительный прием.

б) После этого рассматривается развернутая запись умножения числа на однозначное;

284 · 3 = (200 + 40 + 8) · 3 = 600 + 120 + 24 = 744.

в) Показывается краткая запись этого вычислительного приема в столбик:

×	248
	3
	744

Если ребенок затрудняется сразу перейти от развернутой формы записи к краткой (в этом случае промежуточные результаты необходимо «держать в уме»), то можно порекомендовать использование полуразвернутой записи:

×	248
	3
+ +	600
	120
	24
	744

Деление на однозначное число

Опорными знаниями для этого приема служат: правило деления суммы на число, деление с остатком, табличное умножение и деление, сложение и вычитание двузначных чисел, разрядный состав многозначных чисел.

Развернутая запись приема выглядит следующим образом:

867 : 3 = (600 + 240 + 27) : 3 = 600 : 3 + 240 : 3 + 27 : 3 = 200 + 80 + 9 = 289.

Однако трехзначное число заменить суммой удобных слагаемых (так, чтобы каждое делилось без остатка на данное число) уже значительно сложнее, чем двузначное. Этим обосновывается переход к краткой записи приема.

Краткая запись деления «углом» выполняется по алгоритму:

–	867	3
	6	289
‗	26
	24
‗	27
	27
	0

1) Узнаем, сколько цифр будет в частном. Для этого найдем первое неполное делимое – 8 сотен. Значит, в частном будет три цифры (на месте этих цифр ставим тири точки.)

2) Найдем первую цифру частного. Для этого первое неполное делимое (8 сотен) разделим на 3, получим 2 сотни (записываем эту цифру в частном.) Узнаем, сколько сотен разделили. 2 сотни умножим на 3, получим 6 сотен. Узнаем, сколько сотен осталось. Из 8 сотен вычтем 6 сотен, останется 2 сотни. Остаток меньше делителя, значит первая цифра частного подобрана верно.

3) Найдем вторую цифру частного. (Оставшиеся две сотни дробятся в десятки и процесс повторяется, но уже не с сотнями, а с десятками.) В итоге находим вторую цифру частного.

4) Аналогично находится третья цифра частного.

Тема: Умножение и деление на двузначное число

План:

1. Теоретическая основа приемов умножения на двузначное и трехзначное число.

2. Умножение и деление на двузначное число.

3. Умножение и деление на трехзначное число как обобщение алгоритмов письменного умножения и деления.

4. Виды упражнений для совершенствования вычислительных навыков.

5. Формирование навыков письменного умножения и деления многозначных чисел на двузначное (трехзначное) число, использование приемов:

- обучение подбору цифр частного;

- нахождение цифр частного;

- приемы проверки пробной цифры частного;

- предупреждение ошибок учащихся при умножении и делении многозначных чисел;

- случай деления с нулем в частном;

- приемы самоконтроля при выполнении умножения и деления многозначных чисел.

6. Анализ альтернативных подходов.

Рекомендательная литература

1. Гребенникова Н.Л. умножение и деление многозначных чисел: Учебно-методическое пособие для учителей и студентов. – Стерлитамак: Стерлитамак. гос. пед. ин-т., 1996. – С. 91.

2. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: ЛИНКА-ПРЕСС, 1997. – С. 288.

3. Урок в системе развивающего обучения: Из опыта работы / под ред. Дусавицкого А.К. – Харьков, 1998. – С. 61.

Это самая объемная тема в 4 классе. В результате ее изучения дети должны приобрести прочные навыки умножения и деления в столбик на однозначное, двузначное и трехзначное число, а также знать свойства арифметических действий, которые обосновывают данные вычислительные приемы.

Эта тема изучается в определенной последовательности.

Умножение и деление многозначного числа

на однозначное

Данная тема уже рассматривалась в 3 классе на примере умножения и деления трехзначного числа на однозначное. Опираясь на имеющиеся у ребенка знания соответствующих алгоритмов, можно легко их распространить на любые многозначные числа. При этом следует учесть, что первый шаг алгоритма связанный с определением количества цифр в частном и их фиксацией в виде точек, имеет большое значение для предупреждения ошибок при выполнении деления в случаях, когда в записи частного содержатся нули:

–	432		4
	4		108
	–	32
		32
	0

В этом случае дети часто пропускают в частном цифру 0 и вместо ответа 108 получают 18.

Умножение чисел, оканчивающихся нулями

На подготовительном этапе к изучению данного приема дети знакомятся с правилом умножения числа на произведение, которое выполняет роль теоретического обоснования. Рассмотрим пример умножения числа на произведение 3 (4 · 2), необходимо раскрыть три способа нахождения результата:

1. 3 · (4 · 2) = 3 · 8 = 24;

2. 3 · (4 · 2) = (3 · 4) · 2 = 24;

3. 3 · (4 · 2) = (3 · 2) · 4 = 24.

Для иллюстрации данного правила можно обратиться к подсчету кубиков в прямоугольном параллелепипеде размером 3 × 4 × 2 кубика. Каждому способу умножения числа на произведение соответствует определенный способ подсчета кубиков в параллелепипеде.

После этого можно переходить к развернутой записи умножения чисел, оканчивающихся нулями:

621 · 30 = 621 · (3 · 10) = 621 · 3 · 10 = 1863 · 10 = 18630.

Однако устно выполнить это умножение сложно, поэтому осуществляется переход к краткой записи, опирающейся на

×	621
	30
	18630

Аналогично выполняется умножение чисел, содержащих нули в каждом множителе:

×	5230
	60
	313800

Таким образом, изучение каждого нового вычислительного приема опирается на уже ранее освоенные ребенком приемы.

По аналогичной схеме изучается деление чисел, оканчивающихся нулями, умножение и деление на двузначное и трехзначное число. Теоретическим обоснованием деления чисел, оканчивающихся нулями, служит правило деления числа на произведение.

Нахождение цифр частного при делении

многозначных чисел

Письменные вычисления, как правило, в преобладающем большинстве III – IV классов усваиваются учащимися удовлетворительно. Наиболее трудными оказываются действия над многозначными числами с нулями в компонентах и результатах действий, и поэтому наибольшее число ошибок встречается именно в этих действиях.

Причина их – недостаточное усвоение учащимися нумерации многозначных чисел. Для предупреждения таких ошибок учителя должны добиваться, чтобы перед переходом к действиям с многозначными числами учащиеся хорошо усвоили состав многозначных чисел, представление числа в единицах различных разрядов.

Наиболее трудным для учащихся начальной школы является

деление многозначных чисел на двузначное и трехзначное. Массовым видом ошибок учащихся при выполнении этого арифметического

-	3681	9
	36	49
81
81
0

- пропуск нуля в частном (409).

―	64454	67
	603	9512
―	415
	335
	80
	67
―	134
	134

- неверно подписано число 415, ошибка в подборе частного – цифра 5.

Причиной таких ошибок является не только недостаточное усвоение учащимися техники деления многозначных чисел, но и неумение определить наивысший разряд частного, первое неполное делимое. В первом случае, разделив 3 тысячи на 9 единиц, ученик получил только 49 единиц, хотя деление 3 тысяч даже на 10 дает 300 единиц, а если делить на 9, то результат будет еще больше. И во втором случае примерный подсчет деления 64 тысяч на 67 должен подсказать, что частное не может быть больше тысячи.

Итак, предварительная прикидка частного является очень важным практическим навыком самоконтроля, предупреждающим многие грубые ошибки при делении многозначных чисел.

Для предупреждения таких ошибок можно учить учащихся сразу определять, какой примерно наивысший разряд должны они получить в частном, исходя из наивысшего разряда делимого и делителя. Так, перед выполнением деления во втором примере ученик может определить, что частное не должно быть больше тысячи.

Навыки письменного деления чисел на двузначное число и особенно на трехзначное у учащихся, закончивших начальную школу, не всегда соответствуют требованиям. Об этом свидетельствует многих учителей, ведущих математику в IV классе, а также результаты проверочных работ.

Трудности в подборе цифр частного не только сказываются на времени, затрачиваемом на выполнение задания, но часто приводит к тому, что учащиеся теряют уверенность в своих силах и не могут закончить решение одного примера и приступить к решению следующего.

Однако, можно подготовить учащихся к решению примеров данного вида, если вести для этого специальную работу.

Нахождение верной цифры частного – составная часть алгоритма письменного деления многозначных чисел. Выполнение этой операции включает в себя:

1. нахождение пробной цифры частного,

1. проверка найденной пробной цифры.

Остановимся на рассмотрении первого из этих этапов.

При нахождении пробной цифры частного учащиеся должны уметь, во-первых, округлить делитель до одной значащей цифры и, во-вторых, разделить неполное делимое на полученное число, оканчивающееся нулями. В учебнике математике автора М.И. Моро неявно используется прием округления, однако обучение этому программой не предусмотрено. Кроме этого, специальное изучение показало, что большинство учащихся не пользуются приемом округления делителя и делимого.

Учащиеся быстрее находят цифру частного, если при нахождении пробной цифры они округляют делитель до ближайшего круглого числа, меньшего или большего его. Они могут выполнять округление на основании знания расположения чисел в натуральном ряду, правила образования числа. Поэтому, мы считаем нужным, при выполнении письменного деления округлять делитель до ближайшего круглого числа. Это способствует рационализации вычислений, так как учитель формирует у учащихся не только прочные, но и рациональные вычислительные навыки.

При изучении деления на трехзначное число полезно включать в устную работу с учащимися упражнения вида:

1. Округление до ближайшего круглого числа.

1. Сколько сотен, десятков, единиц в числе: 238, 368, 850?

2. Между какими ближайшими числами, оканчивающимися двумя нулями, находится число: 238, 368, 644, 850?

3. К какому из чисел:

• 100 или 200 ближе число 238;

• 300 или 400 ближе число 368;

• 600 или 700 ближе число 644;

• 300 или 400 ближе число 850?

4. Замени каждое из чисел: 238, 368, 644, 850 ближайшим числом, оканчивающимся двумя нулями.

   2. На нахождение цифры частного.

Найди частное:

80 : 20 94 : 30 600 : 200 823 : 200

140 : 70 547 : 60 1 200 : 300 1 656 : 400

160 : 50 674 : 80 1 700 : 500 1 368 : 600

Устные упражнения приведенного вида помогут сформировать умение рационально находить цифры частного.

Прием подбора цифры частного знаком учащимся еще со 2^го класса, когда они знакомятся с конкретным смыслом деления:

12 : 3 =?

Какое число нужно подобрать, чтобы при умножении на 3 получилось 12?

В 3 ^ем классе в теме «Внетабличное умножение и деление» учащиеся дважды встречаются с этим приемом: при подготовке к делению, вида

80 : 40 = - какое число надо умножить на 40, чтобы получилось 80?

и делении двузначного числа на двузначное вида 95 : 19 - можно делать прикидку частного путем округления делимого и делителя:

Так как 95 ≈ 100

19 ≈ 20, то пример 95 : 19 можно заменить примером

100 : 20=5, затем эту цифру проверить:

5  19=19  5=95.

Если в дальнейшем не упускать ни одной детали в кропотливой подготовительной работе к изучению деления многозначных чисел, можно предупредить многие ошибки учащихся.

Большинство учащихся, определяя цифры частного, пользуются либо табличным умножением, либо формально заучив алгоритм письменного деления, опираются на количество цифр делителя:

793	21

- так как в делителе 2 цифры, сначала делят 79 на 21.

Чаще всего учащиеся находят цифру частного перебором – исправление цифр в работах учащихся подтверждают этот характер ошибки.

Однако, в традиционном обучении дети имеют достаточные знания для ознакомления с приемом округления делимого и делителя и применения его в вычислениях.

Определяя необходимые для этого теоретические знания, учитель сможет подобрать соответствующие подготовительные упражнения.

Так, выполняя деление вида

2208	48

Определяем первое неполное делимое: так как делитель равен 48, то 22 сотни нельзя разделить на 48, чтобы получилась хотя бы одна сотня. Будем делить десятки: в числе 220 десятков. Этот шаг алгоритма выводит учителя на упражнения, в которых нужно определить общее количество единиц каждого разряда и отдельных единиц каждого разряда:

• прочитайте число 2208

• сколько в нем всего единиц? отдельных единиц?

• сколько в числе всего десятков? отдельных десятков?

• сколько в числе всего сотен? отдельных сотен?

Выполняем деление 220 : 48 – на этом этапе применим прием округления. Дети определяют:

220 это число близкое к 200, а

48 находится ближе к 50.

Здесь, как и в предыдущем задании при округлении обоих чисел удобно ориентироваться на натуральный ряд чисел. Эти знания учащиеся применяют с 1^го класса. На уроке можно вспомнить их.

Между какими круглыми числами находятся числа:

228, 2208, 22080?

200 < 220 < 228 < 230 < 250

2000 < 2200 < 2208 < 2300 < 3000

22000 < 22080 < 22100.

Следующий вид задания, который представляет собой теоретическую основу подготовки учащихся – это деление круглого числа на круглое число. Предварительно можно выполнить задание –

Уменьшить в 10 раз, в 100 раз следующие числа:

220 2200

180 180.

Как это делать?

После этого – связанное с ним задание. Выполните деление:

220 : 20 2200 : 200

180 : 20 1800 : 200

Как это сделать?

Предложенные задания имеют в своей основе следующие знания нумерации: разрядный состав многозначного числа, поместное значение цифры в записи числа, умение находить место числа в числовом ряду, уменьшение числа в 10, 100, 1000 раз. Для выполнения последнего задания повторяется правило деления по частям – сначала делим на 10 (или 100), затем на однозначное число:

220 : 20 = 220 : (10  2) = 220 : 10 : 2 = 22 : 2 = 11.

Акцентрируя внимание на подготовительных заданиях, мы подчеркиваем еще раз то, что эту работу нужно вести еще задолго до обучения младших школьников письменному делению многозначных чисел на двузначное и трехзначное число. Еще при изучении нумерации в каждом классе можно выполнять приведенные выше задания. Тогда они станут не просто подготовительными упражнениями, в них заключается теоретическая основа вычислительного приема округления делимого и делителя. При систематической работе учителя над подготовкой к обучению деления многозначных чисел эти теоретические знания постепенно сформируются в вычислительный навык.

Этот навык можно развивать в следующих заданиях:

Не выполняя деления, сравни пары примеров

19488 : 48 = 22080 : 48 =

49488 : 48 = 52080 : 48 =

Чем они отличаются?

Чем отличаются результаты в каждой паре примеров?

После большой подготовительной работы рассуждения учащихся могут принять такой вид:

19 488	48

194 ≈ 200

48 ≈ 50

200 : 50 = 200 : (10  5) = 200 : 10 : 5 = 20 : 5 =4.

Выполняя действия, учащиеся устно выполняют округление, деление на круглое число, определяют пробную цифру в частном, проверяем ее.

В алгоритме письменного деления этот этап, на наш взгляд, самый трудный. Поэтому большое внимание мы уделяем подготовительной работе, делая вычисления осознанными, прочными. Учащиеся постепенно учатся округлять не только до круглых сотен.

534264	89

В данном случае удобнее округлить делимое и делитель так, чтобы свести к табличному случаю при помощи следующих рассуждений:

534 ≈ 540

89 ≈ 90

540 : 90 = 540 : (10  9) = 540 : 10 : 9 = 54 : 9 = 6.

Ученики подыскивают такое число, чтобы деление можно было свести к табличному. То есть 534 удобно округлять не до 500, а до 540, чтобы затем разделить на 90.

На последующих уроках до того, как приступить к основной работе наиболее полезными являются группы примеров:

1. Найди пробную цифру частного, округляя делимое и делитель до ближайшего круглого числа:

67 : 31 396 : 124

168 : 53 2 315 : 431

145 : 69 4 253 : 682

294 : 87 2 038 : 893

2. Найдите частное:

56 : 14 288 : 72

92 : 23 415 : 83

72 ; 18 268 : 67

78 : 39 891 : 99

Характер приведенных заданий выявляет еще одну важную проблему к 4 классу: усложняется теория, арифметические выражения, достаточно сложна терминология, которой овладевают учащиеся.

Неумение четко и лаконично, правильным языком формулировать умозаключения свидетельствует о недостаточном математическом языке учащихся. Устный опрос учащихся показывает, что в большинстве случаев учащийся понимает смысл подбора тех чисел, над которыми производит действия, но не умеет правильно изложить свои соображения.

Для предупреждения таких ошибок опытные учителя проводят большую и настойчивую работу по развитию математического языка учащихся. Не ограничивая учащихся выбором одного из способов решения, опытные учителя систематически приучают учащихся искать наиболее рациональные способы решения задач.

Такая устойчивая, продуманная во всех деталях работа учителя над формированием навыков деления дает хорошие результаты.

МЕТОДИКА ИЗУЧЕНИЯ ОСНОВНЫХ ВЕЛИЧИН

В НАЧАЛЬНОМ КУРСЕ МАТЕМАТИКИ (8 часов)

План:

Общие вопросы изучения величин:

- этап актуализации знаний (уточнение представлений у младших школьников о данной величине);

- ознакомление с величиной на основе сравнения однородных величин;

- знакомство с единицей измерения данной величины и с измерительным прибором;

- выполнение упражнений по измерению, сравнению однородных величин;

- сложение и вычитание однородных величин, выраженных в единицах одного наименования;

- знакомство с новыми единицами данной величины, перевод одних единиц в другие;

- сложение и вычитание однородных величин, выраженных в единицах двух наименований;

- умножение и деление величины на число.

Рекомендательная литература

1. Истомина Н.Б. Знакомство с величинами // Начальная школа. – 1983. - №1. – С. 32-35.

2. Виленкин Н.Я., Петерсон Л.Г. Математика, 1 класс. – Часть 3: Учебник для 1-го кл. – М.: «Баласс», 1996. – 96 с.

3. Петерсон Л.Г. Математика, 1 класс: методические рекомендации. Пособие для учителей. – М.: «Баласс», 1996. – С. 118-136.

4. Игнатова Л.В. Формирование представлений о зависимости величин в курсе начальной математики // Начальная школа. – 1985. - №7. – С. 36-38.

5. Холомкина А.И. Изучение мер времени // Начальная школа. – 1988. - №3. – С. 48-51.

6. Депман И.Я. Мир чисел. – Л., 1975.

7. Степанова С.В. Тема «Величины» в курсе математики для 1-го класса // Начальная школа. – 1989. - №8. – С. 39-44.

Тема: Методика изучения длины

План:

1. Порядок изучения темы:

а) подготовительный этап;

б) ознакомление с понятием «длина»;

в) введение первой единицы измерения длины «сантиметр» и обучение измерению длины с помощью линейки;

г) упражнения на закрепление [13];

д) ознакомление с дециметром (упражнения на закрепление);

е) ознакомление с метром (упражнения на закрепление);

ж) ознакомление с километром (выписать задания на измерение расстояний).

2. Сделать анализ наглядных пособий.

3. По каждому пункту найти ответ по учебникам математики.

4. Приведите примеры упражнений, используемых для раскрытия свойств величин.

Рекомендательная литература

1. Король Я.А. Измерение длины отрезков // Начальная школа. – 1982. - №10. – С. 51-53.

2. Холомкина А.И. Изучение мер длины в 1-2-х классах // Начальная школа. – 1981. - №9. – С. 37-41.

В начальной школе дети знакомятся с четырьмя основными величинами (длина, масса, время, площадь). В 1 классе начинается систематическое изучение длины и осуществляется первичное знакомство со временем. Рассмотрим более подробно методику работы над длиной.

Методика работы над длиной и ее измерением

В методике работы над длиной можно выделить несколько самостоятельных этапов.

На первом этапе уточняются уже имеющиеся у ребенка представления о длине и термин «длина» вводится в его активный словарь. Для этого используется метод приложения одного предмета линейной протяженности к другому (например, карандаша к ручке). Как правило, результат этого сравнения ребенок уже может выразить с помощью слова «длина». Если же в его речи доминирует более широкий термин «больше», то его можно дифференцировать: «В этом случае говорят, что длина карандаша больше, чем длина ручки». Таким образом, смысл термина «длина» у ребенка ассоциируется с линейной протяженностью предмета. Чем предмет протяженнее, тем его длина больше.

На втором этапе моделируется ситуация, в которой предыдущий прием сравнения путем приложения одного предмета к другому уже не срабатывает. Дл этого можно на разных краях стола положить две полоски бумаги примерно одинаковой длины (чтобы их было трудно сравнить «на глаз») и попросить ребенка сравнить их длины, соблюдая условие: приближать полоски друг к другу нельзя. После ряда попыток совместно с ребенком выводим несколько новых приемов сравнения длин: а) с помощью веревочки (прикладывая ее сначала к одной полоске, а затем к другой); б) с помощью короткой полоски-мерки, укладывая ее сначала вдоль первой полоски, а затем вдоль второй; в) наконец, можно перевернуть полоски обратной стороной и пересчитать на них заранее нанесенные через один и тот же промежуток метки (если, например, в первой полоске таких меток 8, а во второй 9, то длина второй полоски больше, чем первой).

На третьем этапе сначала пересчитываем метки на полосках (например, на первой полоске таких меток 15, а на второй – 16)). Делаем вывод: длина второй полоски больше. Однако прикладывая ее к первой, убеждаемся, что она наоборот, короче первой. В чем же дело? Оказывается метки на полосках нанесены через промежутки различной длины, т.е. мерки разные. Вывод: при сравнении длин нужно пользоваться одинаковыми мерками. Тем самым мотивируется введение стандартной единицы измерения длины – 1 см. В качестве материального носителя этой единицы длины удобно использовать модель вырезанного из картона квадратика со стороной 1 см.

На четвертом этапе ребенку можно предложить измерить длину нескольких предметов, выкладывая вдоль них модели квадратиков со стороной 1 см. Тем самым будет раскрыт смысл измерения величины как процесса ее сравнения с однородной величиной, принятой за единицу измерения. При этом можно подвести ребенка к самостоятельному выводу, что результат измерения от того, какая мерка для этого была выбрана.

На пятом этапе знакомим ребенка с линейкой как инструментом, с помощью которого измеряется длина. В соответствии с последними изменениями программы, в содержание 1 класса вновь включено понятие отрезка. Поэтому уже в 1 классе отрезок начинает выполнять роль «геометрического носителя», на котором отрабатывается умение измерять длину отрезка. Это умение в дальнейшем будет востребовано при вычислении периметра и площади многоугольника.

На заключительном этапе, в конце учебного года, вводится вторая единица измерения длины – дециметр. Необходимость введения новой единицы мотивируется неудобством использования сантиметра при измерении больших расстояний (например, длины крышки стола). С помощью дециметра этот процесс осуществляется быстрее. Вводится соотношение между этими единицами: 1 дм = 10 см. на данном этапе основная функция изучения этих единиц измерения длины состоит в том, чтобы способствовать усвоению нумерации чисел второго десятка. Ведь дециметр – это хорошая модель десятка, а сантиметр – единицы. Поэтому перевод одной единицы измерения в другую обогащает опыт ребенка при изучении разрядного состава двузначных чисел в пределах 20.

Таким образом, заканчивая 1 класс, ребенок должен иметь представления о длине как одной из величин, понимать смысл измерения длины как процесса сравнения ее с однородной величиной, принятой за единицу измерения, знать две единицы измерения длины (сантиметр и дециметр) и соотношение между ними, уметь измерять длины конкретных предметов и отрезков.

Такая величина как время, в 1 классе вводится только в ознакомительном порядке. Ребенок должен научится определять время по часам с точностью до часа (минута и ее соотношение с часом по программе не вводится).

Проверочные задания по теме «Изучение величин»

1. Поставь знаки >, < или =:

1 дм …3 см; 8 см …2 дм; 1 дм 4 см …15 см.

2. Впиши нужные числа:

1 дм = … см; 1 дм 7 см = … см; 19 см = … дм … см.

Во в 2 классе продолжается работа над такими величинами как длина, время, масса.

При изучении длины водится третья единица измерения – метр. Потребность в обращении к этой единице мотивируется неудобством прежних единиц (сантиметра и дециметра) при измерении больших расстояний (например, длины класса). Кроме того, все три единицы активно используются при изучении нумерации чисел в пределах ста (2 класс) и в пределах тысячи (3 класс). Метр в этом отношении может рассматриваться в качестве модели сотни, дециметр – модели десятка, а сантиметр – модели единицы. Перевод одних единиц измерения в другие служит для ребенка хорошей практикой в усвоении разрядного состава двузначных и трехзначных чисел. Уже на данном этапе ребенок усваивает соотношение между изученными единицами длины:

1 дм = 10 см; 1 м = 10 дм; 1 м = 100 см.

В изучении другой величины – времени – в качестве новой единицы измерения выступает минута. Ребенок должен уметь определять время по часам уже с точностью до минуты. Так как 1 ч = 60 мин, то перевод составных единиц в простые и обратно (например, 1 ч 28 мин = 88 мин; 92 мин = 1 ч 32 мин и др.) также помогает в усвоении разрядного состава двузначных чисел. Однако в отличие от единицы длины, в изучении мер времени есть одна особенность: в ее основе лежит шестидесятеричная система счисления. Это является причиной одной из самых распространенных ошибок при работе с мерами времени, когда при переводе часа в минуты ребенок считает, что 1 ч = 100 мин. Поэтому на данный факт следует обратить особое внимание

Тема: Методика изучения темы «Площадь»

План:

1. Методика изучения темы «Площадь»:

а) подготовительный этап;

б) ознакомление с понятием «площадь»;

в) введение первой единицы измерения площади «квадратный сантиметр»;

г) обучение измерению площади с помощью палетки;

д) методика ознакомления с правилами вычисления площади прямоугольника;

е) закрепление (выписать наиболее значимые упражнения);

ж) ознакомление с квадратным дециметром;

з) ознакомление с квадратным метром.

Выполнить задания:

1. По каждому из пунктов составить фрагменты уроков, подготовиться к их проведению.

Рекомендательная литература

1. Царева С.Е. Первые уроки по изучению площади // Начальная школа. – 1981. - №10. – С. 39-42.

2. Абдуллаев К.О. О подготовке учащихся к усвоению понятия площади // Начальная школа. – 1978. - №9. – С. 17-20.

3. Салихова М.О. О дифференциации понятия «периметр» и «площадь» фигуры // Начальная школа. – 1981. - №10. – С. 42-44.

Площадь фигуры, единицы измерения

Данную тему изучают в следующей последовательность.

1) Уточнение представлений о площади. Для этого можно взять две плоские фигуры и наложить одну на другую так, чтобы первая целиком помещалась во второй.

В этом случае говорят, что площадь первой фигуры меньше площади второй фигуры.

2) Моделируется ситуация, когда ни одна из плоских фигур в другой целиком не помещается (т.е. метод наложения, который использован на предыдущем этапе, уже не работает). Как быть в этом случае? Для этого фигуры предварительно с обратной стороны расчерчиваются на одинаковые квадратики. Переворачиваем и подсчитываем квадратики в каждой фигуре. Та фигура, в которой количество квадратиков больше, имеет большую площадь.

3) На данном этапе моделируется ситуация, которая похожа на предыдущую. Однако в ней первая фигура хотя и имеет больше квадратиков, но целиком помещается во второй. Как такое могло произойти? Причина в том, что во второй фигуре квадратики большего размера. Вывод: для сравнения площадей нужны одинаковые квадратики. Этим мотивируется введение стандартной единицы измерения площади – 1 см².

4) Измерение площади произвольной фигуры с помощью пленки на ней сеткой квадратных сантиметров.

5) Изучение правила вычисления площади прямоугольника.

6) Введение новых единиц измерения площади – 1 дм² и 1 м². Необходимость введения этих единиц мотивируется тем, что квадратным сантиметром измерять площади больших фигур неудобно. Особое внимание следует обратить на соотношение квадратных единиц, т.к. дети его часто путают с соотношением линейных единиц.

Тема: Методика изучения темы «Масса»

План:

1. Порядок работы над темой.

2. Система упражнений по формированию представления о масса на основе сравнения различных значений однородных величин.

3. Последовательность упражнений, формирующих представление о массе.

4. Подготовительный урок – экскурсия в магазин, школьную столовую.

Рекомендательная литература

1. Истомина Н.Б. Знакомство с величинами // Начальная школа. – 1983. - №1. – С. 32-35.

2. Тихоненко А.В. Формирование представлений о массе тел и емкости // Начальная школа. – 1990. - №6. – С. 75-79.

Во 2 классе учащиеся знакомятся еще с одной величиной – массой. показываем ребенку две абсолютно одинаковые на вид картонные пачки (из-под макарон или других кулинарных изделий) и просим ответить на вопрос, чем они отличаются. внимательно осмотрев пачки, ребенок приходит к выводу, что они одинаковы. Тогда предлагаем каждую пачку взять в руку и сравнить ее на вес. «Эта пачка тяжелее» - сразу же определяет ребенок (предварительно необходимо одну из пачек аккуратно вскрыть, часть ее содержимого отсыпать и вновь заклеить). «В этом случае говорят, что масса первой пачки больше, чем масса второй» - поясняет взрослый. В дальнейшем этот термин активно используется в речи ребенка. (следует отметить, что термин «вес» в настоящее время из математической терминологии исключен.) в качестве первой единицы измерения массы вводится килограмм. С помощью этой единицы ребенок учится (желательно на чашечных весах) определять массу различных предметов.

МЕТОДИКА ИЗУЧЕНИЯ ЭЛЕМЕНТОВ ГЕОМЕТРИИ

В НАЧАЛЬНОМ КУРСЕ МАТЕМАТИКИ (4 часа)

Тема: Методика изучения элементов геометрии в начальном курсе математики

План:

1. Задачи изучения геометрического материала.

2. Общие вопросы методики работы над геометрическим материалом.

3. Задачи геометрического содержания.

4. Формирование представлений и понятий о геометрических фигурах:

- существенные и несущественные признаки;

- содержание и объем понятия;

- классификация понятий.

5. Последовательность работы по подготовке и изучению периметра прямоугольника (квадрата):

- выяснение общих представлений младших школьников о прямоугольнике;

- знакомство с понятием «прямоугольник» на основе суждения понятия «многоугольник»;

- прямые и непрямые углы;

- изучение свойств прямоугольника, практическое их обоснование.

6. Возможные ошибки в рассуждениях учащихся при изучении геометрического материала.

Рекомендательная литература

1. Абдуллаева К. Пути устранения некоторых геометрических ошибок учащихся // Начальная школа. – 1978. - №2. – С. 14-17.

2. Коган Т.Л. Формирование геометрических понятий // Начальная школа. – 1981. - №2. – С. 26-28.

3. Крайнюк В.М. Практическая направленность в изучении геометрического материала // Начальная школа. – 1980. - №1. – С. 4-36.

4. Колягин Ю.М., Тарасова О.В. Наглядная геометрия в начальных классах // Начальная школа. – 1996. - №9. – С. 70-74.

5. Левенберг Л.Ш. Практическая направленность в изучении геометрического материала // Начальная школа. – 1982. - №10. – С. 47-50.

6. Пазушко Ж.И. Развивающая геометрия в начальной школе // Начальная школа. – 1999. - №1. – С. 93-95.

7. Савенков А.И. Задачи для развития объемно-пространственного мышления школьников // Начальная школа. – 1998. - №7. – С. 59-63.

8. Шмырева Г.Г. Практические работы при ознакомлении с геометрическими фигурами в 1-м классе // Начальная школа. – 1982. - №10. – С. 54-57.

Последние изменения программы по математике в начальной школе характеризуются тенденцией усиления внимания к изучению геометрического материала. Так, уже в 1 классе дети знакомятся с такими геометрическими фигурами как точка, линия (прямая, кривая), отрезок, ломаная, многоугольник и его элементы (углы, вершины, стороны). изучение перечисленного геометрического материала не вызывает, как правило, каких либо затруднений у детей.

Начальный период адаптации – примерно один месяц – совпадает с проведением подготовительной работы к восприятию понятий числа, отношения, величины и др.

В начальном курсе математики его называют дочисловым периодом. Дети в этот период учатся целенаправленно проводить наблюдения над предметами и группами предметов, расположением их в пространстве, сравнение по одному или нескольким признакам. Одновременно с обобщением их жизненного опыта, расширением математического кругозора, обучение их организованности, самостоятельности. Большое внимание на этом этапе уделяется развитию математической речи детей, что способствует развитию у них логических умений.

Младший школьник начинает входить в учебную деятельность. На этом этапе следует уделять большое внимание развитию пространственных представлений у первоклассников, в содержание которого входит геометрический материал. Учителя недооценивая его знания уделяют недостаточно времени изучению геометрических фигур. В результате к концу обучения у ребенка слабо сформированы чертежные навыки, умение выделять и обосновывать свойства геометрических фигур, решать простейшие задачи на построение.

Поэтому в работе с первоклассниками изучение первых геометрических понятий можно включить в этот период. Изучение их может проходить не только на уроках в классе, но и на уроках – играх с использованием самого разного дидактического материала, на уроках – экскурсиях (в парках, на улицах города, на пришкольном участке, при проведении подвижных игр с различными заданиями). На геометрическом материале могут быть рассмотрены следующие вопросы программы:

1. Признаки предметов, сравнение предметов по цвету, размеру, форме;

2. Пространственные представления, взаимное расположение предметов;

3. Счет предметов.

Тем самым обеспечивается накопление обобщения жизненного опыта ребенка, реальных ярких впечатлений, которые очень важны для познания детьми окружающего.

Проведенные занятия, наблюдения необходимо осмыслить первоклассникам вместе с учителем, обобщены, включены в формирующуюся систему представлений ребенка о мире. Оптимальные условия для всего перечисленного создают уроки изучения геометрического материала.

Первые дни ребенка в школе не проходят гладко, без стрессов. Задача учителя на этом этапе работы сделать его менее болезненным для психики первоклассника. Одним из способов в этом видится в использовании его резервных возможностей, его жизненного опыта: желание ребенка быть самостоятельным, организованным, умение играть с ровесниками, проявление инициативы.

Уроки математики в период адаптации ребенка к обучению представляют ему наилучшую возможность. Здесь можно на основе выше перечисленных свойств личности ребенка, обобщении, уточнении его представлений о данном понятии познакомить с новыми. С этой целью проанализируем урок математики, проведенный по теме «Прямая. Кривая. Отрезок.»

Прямая. Кривая. Отрезок.

Цель урока:

1. На основе обобщения жизненного опыта ребенка сформировать представления о геометрических фигурах (точка, прямая, кривая, отрезок).

2. Развивать у первоклассников мыслительные операции (сравнение, умение обобщать, находить закономерность),

3. Связать полученные знания с окружающими предметами.

Оборудование: магнитная доска с набором цветных магнитов – «точек», линейка, шнур, ленты разного цвета, ножницы, у каждого ребенка на столе – цветные полоски из бумаги.