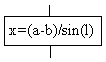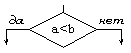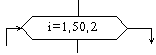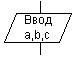Лекция 8. Алгоритм его свойства и формализация. Принципы разработки алгоритмов и программ для решения прикладных задач.

Развитие понятия «алгоритм». Исполнитель алгоритма. Графическое представление алгоритма. Свойства алгоритма. Понятие алгоритмического языка. Формализация понятия «алгоритм»: постановка задачи; машина Поста; машина Тьюринга; нормальные алгоритмы Маркова; рекурсивные функции. Операциональный подход. Структурный подход. Методология разработки программ для ЭВМ. Основы программирования на языке Паскаль. Разработка программ для решения задач документоведения.

Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть алгоритм.

Алгоpитм — заранее заданное понятное и точное пpедписание возможному исполнителю совеpшить определенную последовательность действий для получения решения задачи за конечное число шагов.

Это — не определение в математическом смысле слова, а, скорее, описание интуитивного понятия алгоритма, раскрывающее его сущность.

Название "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi), жившего в 783—850 гг. В своей книге "Об индийском счете" он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними "столбиком", знакомые теперь каждому школьнику. В XII веке эта книга была переведена на латынь и получила широкое распространение в Европе.

Понятие алгоритма является не только одним из главных понятий математики, но одним из главных понятий современной науки.

В настоящее время понятие алгоритма является, наряду с моделью, одним из ключевых терминов информатики. В общем случае его использование проявлялось и проявляется в различных формах: рецепт приготовления блюда, лекарства, правила составления химических формул, правила дорожного движения. Для нас представляет интерес вычислительный алгоритм.

Распространённые способы представления вычислительных алгоритмов:

1) неформализованными средствами:

• на ограниченном естественном языке (построчная запись);

• информационным графом, узлы которого поставлены, в частности, в соответствие операторам, а однонаправленные дуги — маршрутам передачи информации между ними. Информационный граф позволяет представлять в графической форме последовательные и/или параллельные алгоритмы вычислений;

• в виде графической схемы, формируемой из набора графических символов и/или образов;

2) на алгоритмическом языке программирования.

В большинстве случаев использование неформализованных средств имеет место на этапе разработки алгоритма либо моделирующего алгоритма (алгоритма процесса функционирования системы) с той или иной степенью его детализации.

Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.

Исполнителя хаpактеpизуют:

• сpеда;

• элементаpные действия;

• cистема команд;

• отказы.

Сpеда (или обстановка) — это "место обитания" исполнителя. Напpимеp, для исполнителя Pобота из школьного учебника сpеда — это бесконечное клеточное поле. Стены и закpашенные клетки - тоже часть сpеды. А их pасположение и положение самого Pобота задают конкpетное состояние среды.

Система команд. Каждый исполнитель может выполнять команды только из некотоpого стpого заданного списка — системы команд исполнителя. Для каждой команды должны быть заданы условия пpименимости (в каких состояниях сpеды может быть выполнена команда) и описаны pезультаты выполнения команды.

После вызова команды исполнитель совеpшает соответствующее элементаpное действие.

Отказы исполнителя возникают, если команда вызывается пpи недопустимом для нее состоянии сpеды.

Для наглядного представления решения задачи и построения программ на их основе часто разрабатывают схемы алгоритмов. Схема алгоритма — графическое представление структуры алгоритма, его частей с указанием связей между ними.

Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.

При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.

Название символа	Обозначение и пример заполнения	Пояснение
Процесс		Вычислительное действие или последовательность действий. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Решение		Проверка условий. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.
Модификация		Начало цикла. Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Предопределенный процесс		Вычисления по подпрограмме, стандартной подпрограмме. Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Ввод-вывод		Ввод-вывод в общем виде
Пуск-останов		Начало, конец алгоритма, вход и выход в подпрограмму
Документ		Вывод результатов на печать

Основные свойства алгоритмов следующие:

1.   Понятность для исполнителя — исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма.

2.   Дискpетность (прерывность, раздельность) — алгоpитм должен пpедставлять пpоцесс pешения задачи как последовательное выполнение пpостых (или pанее опpеделенных) шагов (этапов).

3.   Опpеделенность — каждое пpавило алгоpитма должно быть четким, однозначным и не оставлять места для пpоизвола. Благодаpя этому свойству выполнение алгоpитма носит механический хаpактеp и не тpебует никаких дополнительных указаний или сведений о pешаемой задаче.

4.   Pезультативность (или конечность) состоит в том, что за конечное число шагов алгоpитм либо должен пpиводить к pешению задачи, либо после конечного числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с выдачей промежуточных результатов.

5.   Массовость означает, что алгоpитм pешения задачи pазpабатывается в общем виде, т.е. он должен быть пpименим для некотоpого класса задач, pазличающихся лишь исходными данными. Пpи этом исходные данные могут выбиpаться из некотоpой области, котоpая называется областью пpименимости алгоpитма.

Алгоритмические языки представляют собой средства описания данных и алгоритмов решения задач, они разработаны для составления программы пользователем. В настоящее время разработано большое количество языков программирования. Они отличаются друг от друга различными свойствами и областью применения.

Алгоритмический язык (как и любой другой язык) образуют три его составляющие: алфавит, синтаксис и семантика.

Алфавит — это фиксированный для данного языка набор основных символов, т.е. "букв алфавита", из которых должен состоять любой текст на этом языке — никакие другие символы в тексте не допускаются.

Синтаксис — это правила построения фраз, позволяющие определить, правильно или неправильно написана та или иная фраза. Точнее говоря, синтаксис языка представляет собой набор правил, устанавливающих, какие комбинации символов являются осмысленными предложениями на этом языке.

Семантика определяет смысловое значение предложений языка. Являясь системой правил истолкования отдельных языковых конструкций, семантика устанавливает, какие последовательности действий описываются теми или иными фразами языка и, в конечном итоге, какой алгоритм определен данным текстом на алгоритмическом языке.

Основные преимущества алгоритмических языков перед машинными:

• алфавит алгоритмического языка значительно шире алфавита машинного языка, что существенно повышает наглядность текста программы;

• набор операций, допустимых для использования, не зависит от набора машинных операций, а выбирается из соображений удобств формулирования алгоритмов решения задач определенного класса;

• формат предложений достаточно гибок и удобен для использования, что позволяет с помощью одного предложения задать достаточно содержательный этап обработки данных;

• требуемые операции задаются с помощью общепринятых математических обозначений;

• данным в алгоритмических языках присваиваются индивидуальные имена, выбираемые программистом;

• в языке может быть предусмотрен значительно более широкий набор типов данных по сравнению с набором машинных типов данных.

Создание программы предполагает выполнение ряда последовательных этапов:

• постановка задачи;

• математическое описание и выбор метода;

• разработка алгоритма решения;

• составление программы;

• тестирование и отладка программы;

• эксплуатирование программы.

Первый этап представляет собой постановку задачи. На этом этапе формулируется цель задачи, определяется взаимосвязь с другими задачами, раскрывается состав и форма представления входной, промежуточной и результативной информации, характеризуются формы и методы контроля достоверности информации на ключевых этапах решения задачи, определяются формы взаимодействия пользователя с ЭВМ в ходе решения задачи и т.п.

На втором этапе разработки программы выполняется формализованное описание программы, т.е. устанавливаются и формулируются средства языка математики логико-математические зависимости между исходными и результатными данными. Для задач, допускающих возможность математического описания, необходимо выбрать численный метод решения, а для нечисловых задач – принципиальную схему решения в виде однозначно понимаемой последовательности выполнения элементарных математических и логических операций.

Третий этап подготовки решения задачи на ВМ представляет собой алгоритмизацию ее решения, т.е. разработку оригинального или адаптацию известного алгоритма. Алгоритмизация – это сложный процесс, носящий в значительной степени творческий характер. Постановка задачи и ее алгоритмизация составляют до 20-30% общего времени на разработку программы. Сложность и ответственность реализации данного этапа объясняется тем, что для решения одной и той же задачи, как правило, существует множество различных алгоритмов.

Четвертый этап – составление программы. На этом этапе производится перевод описания алгоритма на один из доступных для ЭВМ языков описания.

Тестирование и отладка составляют заключительный этап разработки программы решения задачи на ЭВМ. Оба эти процесса функционально связаны между собой, хотя их цели несколько отличаются друг от друга.

Тестирование представляет собой совокупность действий, предназначенных для демонстрации правильной работы программы. Цель тестирования заключается в выявлении возможных ошибок в разработанных программах путем их проверки на наборе заранее подготовленных контрольных примеров.

Процессу тестирования сопутствует процесс отладки, который подразумевает совокупность действий, направленных на устранение ошибок в программе. Действия по отладке начинаются с момента обнаружения фактов ошибочной работы программы и завершаются устранением причин, порождающих ошибки.

После завершения процессов тестирования и отладки программные средства вместе с сопроводительной документацией передаются пользователю для эксплуатации. Основное назначение сопроводительной документации – обеспечить пользователя необходимыми инструктивными материалами по работе с программой.

Машина Поста (МП) — абстрактная вычислительная машина, предложенная Эмилем Леоном Постом (Emil L. Post) для построения теории алгоритмов. Дело в том, что если задача вообще поддается решению, она непременно может быть запрограммирована для решения на машине Поста. Машина Поста учит алгоритмическому мышлению, интуитивному пониманию сути алгоритма.

Машина Поста представляет собой бесконечную ленту, разделенную на ячейки, вдоль которой движется каретка. Ячейка может быть либо пустой, либо помеченной. На каждом шаге каретка может осуществить лишь одно действие: переместиться на одну ячейку влево или вправо, прочитать содержимое ячейки, проставить или стереть в ней отметку - или остановиться, что означает окончание программы.

Естественно, как и любая другая, машина Поста может потерпеть аварию, которая считается крахом программы. Вот полный список недопустимых действий, ведущих к аварийной остановке машины:

• попытка записать отметку в заполненную ячейку;

• попытка стереть отметку в пустой ячейке;

• уход каретки в бесконечность (вообще говоря, это трудно назвать остановкой, но бессмысленное повторение одних и тех же действий - зацикливание - ничуть не лучше вышеперечисленного).

Программирование машины Поста

Условимся, что каждый шаг программы обозначается номером. Действия каретки будем обозначать так:

• Шаг вправо ?>

• Шаг влево <?

• Записать отметку V

• Стереть отметку Х

• Просмотреть ячейку ? а; b - (эта команда стоит особняком от всех остальных, потому что предоставляет выбор: если ячейка пуста, перейти к шагу а, а если заполнена - к шагу b)

• Завершить выполнение программы и остановиться !

Вот и весь язык программирования. Незамысловат, не так ли? И тем не менее, способен решить любую задачу, поддающуюся алгоритмизации.

Несложный пример

На ленте проставлена отметка в одной-единственной ячейке. Каретка стоит на некотором расстоянии левее этой ячейки. Необходимо подвести каретку к ячейке, стереть отметку и остановить каретку слева от нее.

Сначала попробуем построить алгоритм обычным языком. Поскольку нам известно, что каретка стоит напротив пустой ячейки, но неизвестно, сколько шагов нужно совершить до пустой ячейки, мы можем сразу сделать шаг вправо, проверить, заполнена ли ячейка, после чего повторять эти действия до тех пор, пока не наткнемся на заполненную ячейку. Как только мы ее найдем, мы выполним операцию стирания, после чего нужно будет лишь сместить каретку влево и остановить выполнение программы.

А вот как будет выглядеть то же самое на программном языке:

1. ?>

2. ? 1; 3

3. X

4. <?

5. !

Куда лаконичнее, не так ли?

Машина Тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина Тьюринга является расширением конечного автомата и способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

В состав Машины Тьюринга входит бесконечная в обе стороны лента, разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной Машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния Машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.

Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила, и недетерминированной в противном случае.

Конкретная машина Тьюринга задается перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j→q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_j записывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (H)). Для каждой возможной конфигурации <q_i, a_j> имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

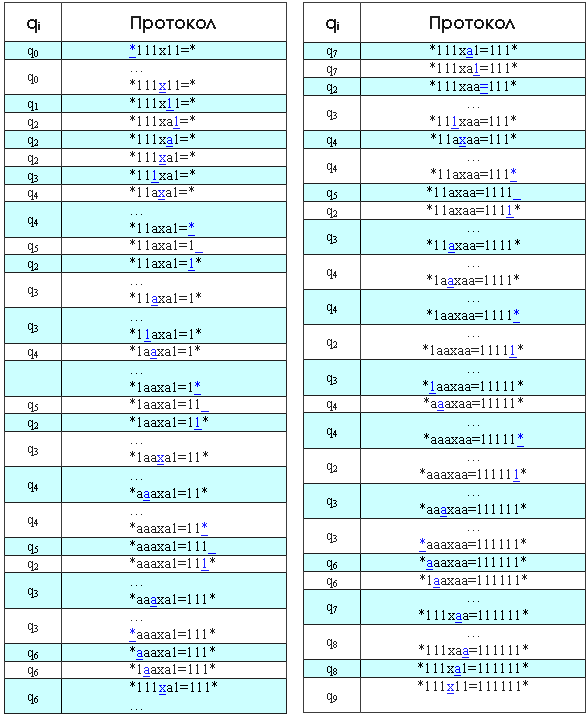
Машина работает по следующему набору правил:

Набор правил	Набор правил	Пример: Умножим с помощью МТ 3 на 2 в единиричной системе
q0*→q0R	q4a→q4aR
q01→q0R	q4=→q4=R
q0×→q1×R	q41→q41R
q11→q2aR	q4*→q51R
q21→q21L	q5^→q2*L
q2a→q2aL	q6a→q61R
q2=→q2=L	q6×→q7×R
q2×→q3×L	q7a→q7aR
q31 → q4aR	q71→q2aR
q3a→q3aL	q7=→q8=L
q3*→q6*R	q8a→q81L
q4×→q4×R	q8×→q9H

Интуитивное понимание машины Тьюринга таково: имеется бесконечная лента, разделённая на клетки. По клеткам ездит каретка. Прочитав букву, записанную в клетке, каретка движется вправо, влево или остаётся на месте, при этом буква заменяется новой. Некоторые буквы останавливают каретку и завершают работу.

Можно сказать, что Машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий. Элементарность действий заключается в том, что действие меняет лишь небольшой кусочек данных в памяти (в случае Машины Тьюринга — лишь одну ячейку), и число возможных действий конечно. Несмотря на простоту машины Тьюринга на ней можно вычислить все, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой.

Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, — это имитация первой машины на второй.

Имитация заключается в следующем. На вход второй машине подаётся описание программы (правил работы) первой машины D и входные данные X, которые должны были поступить на вход первой машины. Нужно описать такую программу (правила работы второй машины), чтобы в результате вычислений на выходе оказалось то же самое, что вернула бы первая машина, если бы получила на вход данные X.

Как было сказано, на Машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

Алгоритм Маркова

Нормальный алгоритм Маркова задается алфавитом и нормальной схемой подстановок, выполняемых по заранее определенной схеме и определяет преобразование строк.

Алфавит - конечное, непустое множество элементов, называемых буквами. Различные сочетания букв образуют слова.

Нормальная схема подстановок - это конечный набор, состоящий из пар слов, где левое слово переходит в правое (но не наоборот).

Нормальным алгоритмом в алфавите А называется следующий алгоритм построения последовательности слов: в качестве начального слова берется само слово Р, и к нему применяют по порядку каждую пару из схемы подстановки. Если подстановка возможна, то ее осуществляют и начинают подстановки сначала. Если процесс обрывается (нет ни одной допустимой подстановки) на слове Q или приходит в конечную подстановку, то данный нормальный алгоритм преобразовал Р в Q.

Если есть задача: от Р перейти к Q и доказано, что нельзя построить нормальную схему, то имеет место алгоритмически неразрешимая задача.

Пример: Дано слово а в алфавите (а,b). Добавить букву b в конец.

Решение:

Введем допольнительный символ - с. Тогда решение будет выглядеть так:

1. сab->aсb // ставим первым в слове символ с и двигаем его в конец слова

2. aсb->abс //

3. abс ->abb // Когда после с уже ничего нет, то меняем ее на b и останавливаемся.

Рекурсия - это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ.

Итерация - способ организации обработки данных, при котором определенные действия повторяются многократно, не приводя при этом к рекурсивным вызовам программ.

Любой алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационном виде, и наоборот.

Структурное программирование учит нас, что есть 5 основных конструкций, из которых как из кубиков строится любая процедура:

SEQUENCE	IF-THEN-ELSE	WHILE-DO	REPEAT-UNTIL	CASE

1. SEQUENCE (Следование). Данной структурой описывается последовательное выполнение каких-то действий в одном направлении. При построении алгоритмов сложных задач целесообразно разбить их решение на ряд укрупнённых этапов вычислений, построить схему из небольшого числа крупных блоков и для каждого из этих блоков разработать собственный алгоритм.

2. IF-THEN-ELSE (Выбор). Описывает выбор одного из нескольких путей ведения вычислительного процесса.

3. WHILE-DO (Цикл с предусловием). Согласно структуре вначале идёт проверка условия. Если оно не соблюдается, управление вычислительным процессом передаётся другой структуре.

4. REPEAT-UNTIL (Цикл с постусловием). Проверка условия происходит каждый раз после выполнения всех действий, предусмотренных в теле цикла. Цикл выполняется до тех пор, пока не будет соблюдено условие.

5. CASE (Оператор выбора). Эта структура позволяет переходить на одну из ветвей в зависимости от значения заданного выражения (селектора выбора).

Основы программирования на языке Turbo Pascal.

Паскаль (Pascal)- учебный инструментальный язык программирования вычислительных машин и персональных компьютеров. Система программирования Turbo Pascal представляет собой интегрированную среду, включающую в себя:

1. Экранный редактор.

2. Компилятор входного языка.

3. Редактор связей.

4. Интерактивный символьный отладчик.

5. Справочную систему.

Указанные компоненты в совокупности обеспечивают поддержку полного цикла разработки программ на языке Turbo Pascal от этапа задания до формирования готового программного продукта. Запуск Turbo Pascal производится командой turbo в командной строке.

TurboPascal

Программа на языке Паскаль состоит из строк. Набор текста программы осуществляется с помощью встроенного редактора текстов системы программирования Турбо Паскаль или любого другого редактора формата DOS.

Существуют различные схемы написания программ на языке Паскаль, все они отличаются количеством отступов слева в каждой строке и различным использованием прописных букв. Схема, которая применяется в данном пособии, имеет следующие черты:

• зарезервированные слова program, procedure, function пишутся строчными буквами;

• имена констант, переменных, процедур, функций начинаются с прописных букв;

• операторы записываются только строчными буквами;

• логически подчиненные структуры записываются на 1 строку ниже и на 1 - 2 позиции правее по отношению к более старшим.

Такая схема, возможно, не является лучшей, но если придерживаться ее, программы будут значительно понятнее, в них значительно быстрее будут "вылавливаться" ошибки.

Максимальный размер программы ограничен. Компилятор позволяет обрабатывать программы и библиотечные модули, в которых объем данных и генерируемый машинный код не превышают 64 Кбайт каждый. Если программа требует большего количества памяти, следует использовать библиотечные модули (.TPU-файлы) или оверлейные структуры.

Примечание. Оверлеи — части машинной программы, которые совместно используют общую область оперативной-памяти. В процессе выполнения программы эти части могут замещать друг друга в памяти.

Синтаксически программа состоит из необязательного заголовка и блока.

Блок может содержать в себе другие блоки. Блок состоит из двух частей: описательной и исполнительной. Первая часть может отсутствовать, без второго - блок не имеет смысла.

Блок, который не входит ни в какой другой блок, называется глобальным. Если в глобальном блоке находятся другие блоки, они называются локальными. Глобальный блок — это основная программа, он должен присутствовать в любом случае. Локальные блоки — это процедуры и функции, их присутствие необязательно.

Объекты программы (типы, переменные, константы и т.д.) соответственно называются глобальными и локальными. Область действия объектов — блок, где они описаны, и все вложенные в него блоки.