4. Индукция и дедукция в обучении математики. Метод математической индукции в курсе математики средней школы.

Умозаключением наз-ся мыслит операция при помощи которой из одного или нескольких известных нам суждений находящихся в определенных смысловой взаимосвязи, получаются новые суждения, содержащие новые по отношению к исходным суждения знания.

Различают два основных вида умозаключений: индукцию и дедукцию.

Термин «индукция» (лат. inductio — наведение, побуждение) - это один из видов умозаключений, при котором из двух или нескольких единичных или частных суждений получают новое общее суждение (вывод);

Пример 1. Единичные суждения:

окружность может пересекаться с прямой не более чем в двух точках; эллипс может пересекаться с прямой не более чем в двух точках; парабола может пересекаться с прямой не более чем в двух точках; гипербола может пересекаться с прямой не более чем в двух точках.

Частные суждения:

Эллипс (в частности, окружность), парабола и гипербола пред­ставляют собой все виды конических сечений, образуя множество кривых второго порядка.

Новое общее суждение:

Кривые второго порядка могут пересекаться с прямой не более чем в двух точках (истинное суждение).

Пример 2. Знакомя учащихся с понятием о высоте тре­угольника, учитель чертит на доске косоугольные треугольники разных видов и в каждом из них проводит высоту; из рассмотрения этих чертежей учащиеся приходят к выводу, что если углы, приле­жащие к основанию треугольника, острые, то высота пересекается с основанием, а если один из двух углов, прилежащих к основанию треугольника, тупой, то высота пересекается с продолжением этого основания.

Первый пример иллюстрирует индукцию как особую форму умозаключения; во втором примере индукция выступает как метод научного исследования, основанный на наблюдении и опыте; в третьем примере индукция выступает в роли метода обучения. Различные формы проявления индукции зависят от характера деятельности, при ко­торой она используется.

Различают два основных вида индуктивных умозаключе­ний: неполную и полную индукцию.

Неполная индукция (как метод исследования) — индукция, при которой не исчерпываются все частные случаи, относящиеся к дан­ной ситуации.

С точки зрения логики неполной индукцией называется умоза­ключение, основанное на рассмотрении одного или нескольких (но не всех) единичных или частных суждений, относящихся к рассматриваемому понятию (или системе понятий).

В процессе обучения неполная индукция проявляется, напри­мер, при изучении переместительного закона сложения, которое ведется по схеме: 5+2 = 2 + 5, значит, а + b = b + а. Такую индукцию часто называют «слабой» индукцией (общий вывод делается после рассмотрения одного (!) примера, вряд ли у кого может возникнуть сомнение в неприемлемости использования «слабой индукции» в обучении математике).

Вывод, основанный на неполной индукции, может быть ошибочным, поэтому индукция в качестве метода исследования применяется весьма осторожно. Значение неполной индукции состоит в том, что рассмотрение частных случаев наводит на мысль о существовании той или иной закономерности, помогает высказать гипотезу о характере этой закономерности; доказательство же справе­дливости сделанного по индукции вывода должно быть осуществлено иным путем (обычно дедуктивным).

Полной индукцией называется умозаключение (вывод), основанное на рассмотрении всех единичных и частных суждений (случаев), относящихся к рассматриваемой ситуации.

Если число этих случаев конечно и все они рассмотрены, то вывод, сделанный посредством полной индукции, можно считать обоснованным.

Так, например, устанавливая число простых чисел в первом десятке, можно рассмотреть все числа первого десятка: 1 = 1; 2 = 1*2; 3=1*3; 4 = 1*4 = 2*2; 5 = 1*5; 6=1*6=2*3; 7=1*7; 8 = 1* 8 = 2* 4 = 2* 2 * 2; 9=1*9 = 3*3; 10 = 1 * 10 = 2 * 5.

Вывод о том, что в первом десятке содержится 4 простых числа, не требует дополнительных обоснований.

Таким образом, заключение, основанное на полной индукции, является вполне достоверным, поэтому полная индукция употребляется и как метод строгого научного доказательства. Однако ею пользуются редко из-за ее громоздкости при большом числе част­ных случаев и редкой возможности применения, когда число част­ных случаев бесконечно. Метод полной индукции можно использовать и тогда, когда число случаев бесконечно. В частности, полная индукция доказательна, если бесконечное множество частных случаев удается разбить на конечное множе­ство взаимно независимых частей.

Т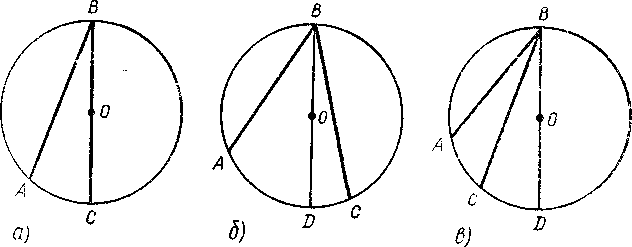 ак, например, изучая вопрос об измерении вписанного утла, обычно рассматривают три случая : а) одна из сторон впи­санного угла является диаметром (для этого случая проводится доказательство); б) диаметр окружности принадлежит вписанному углу; в) диаметр окружности не принадлежит ему (последние два случая легко сводятся к первому). Утверждая, что, доказав спра­ведливость теоремы для каждого из этих случаев, можно считать теорему доказанной в целом, мы применяем принцип полной ин­дукции. Индукция позволяет выдвинуть гипотезу.

Дедукция-“ведение” — форма умозаключения, при которой от одного общего суждения и одного частного получается новое менее общее или частное суждение.

Общее: Если сумма цифр кратна 9, то и само число кратно 9. Частное: У числа 189 сумма цифр кратна 9.

Новое: Число 189 кратно 9. Это дедуктивное умозаключение. Суждения, из которых выводятся новые суждения, называются посылками. Новые суждения, получающиеся из них, наз. заключениями.

Сущность дедукции: данный частный случай подводится под общее положение. Правильность дедуктивного умозаключения зависит от справедливости обоих посылок: если обе посылки верны и правильно применено правило вывода, то заключение бесспорно. Методич особенностью учебника Погарелова явл широкое использование дедуктивного метода.

Дедуктивный метод док-ва теоремы:

Исходя из предыдущих теорем, выводят необходимо вытекающие из них следствия, новые теоремы без рассмотрения частных случаев. В процессе дедуктивного умоз-я выделяют:

1. Большая посылка (аксиомы, ранее доказ. теоремы, определения и все известные утверждения).

2. Малая посылка (данные условия и следствия из них). З. Заключение. Пример:

Д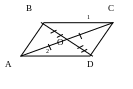 ано: ABCD-четырёхугольник

AB, CD – диагонали;

Доказать: ABCD- параллелограмм.

Док-во: Доказательство разбивается на несколько силлогизмов.

1 силлогизм: (Боьшая посылка): Если две стороны и угол между ними одного соответ-но равны 2-м сторонам и углу между ними другого, то такие -ки равны.

(Малая посылка): Заключение:

2 силлогизм: ( посылка): В равных -ках против равных сторон лежат равные углы.

(Малая посылка): В против лежит . В против лежит . Заключение: .

3 силлогизм: ( посылка): Если при пересечение двух прямых третьей внутренние накрест лежащие углы равны, то прямые параллельны.

(Малая посылка): и - 2 прямые; - секущая; . Заключение: ‌‌׀׀ .

Доказательство для школы:

1. Докажем, что . Находим -ки, в которые входят и , и докажем их равенство.

2. Применим признак равенства треугольников.

Оформление:

1. Случай: 1. Рассмотрим и

- по условию.

- вертикальные.

Следовательно = - по двум сторонам и углу между ними.

…………………

2. Случай: Рассмотрим и

по условию

вертикальные

= по двум сторонам и углу между ними

……………………

Н ередко в цепи доказательств опускается та или иная посылка. В 5-6 классах такие пропуски нужно делать очень осторожно. Дедукция широко используется в 7-11 классах (где почти всё обосновывается). Надо показать, что опыт и наблюдения не всегда дают безошибочные знания. Результаты наблюдения и опыта могут быть приближёно верными или даже ошибочными. Проиллюстрировать зрительные иллюзии:Какой отрезок длинее? Всё, что устанавливается опытным путём подвергается проверке либо доказательству.

Метод математической индукции: Сейчас этот метод из программы ср. школы исключён (в факультативах, в профильных классах и школ с мат. уклоном). Суть: основан на принципе мат-й индукции.

Если какое-либо утверждение, сформул-е для натур. n , проверенное для n=1 и из допущения его истинности для некоторого значения n=k следует его истинность для значения n=k+1, то утверждение имеет место для любого нат. n.

1. Шаг. Проверяется истинность предложения для n=1.

2. Шаг. Допускается, что предложение верно для n=k и исходя из этого доказывается истинность для n=k+1.

3. Шаг. На основание первых двух шагов и принципа мат. индукции, заключается, что теорема верна для всех нат. n.