22. Методика введения понятия функции.

Цель: познакомить учащихся с основными функциональными понятиями и графиками y=k*x+b и y=k*x.

В школе изучение функциональной зависимости делится на два периода 1) 1-6 кл период функциональной пропидевтики. В этот период не водится определение функции, но на конкретном материале, всеми доступными средствами следует формировать идею функциональной зависимости. Этому способствует решение арифметических задач с переменными данными, заполнение таблиц, построение простейших графиков. При решении текстовых задач следует обращать внимание, на функциональные зависимости, которые лежат в основе (например, зависимость между расстоянием, временем и скоростью). Такая пропидевтика позволяет понять, что есть величины, которые могут менять свое значение. С 5 кл. следует готовить учащихся к построению и чтению графиков. Для развития функционального мышления необходимо использовать геометрич материал: нахождение площади, периметра квадрата. Следует готовить учащихся к построению и чтению графиков. (откладывание на луче значений из таблицы). Использовать графики при решении задач типа: путь=скорость*время; масса =удельный вес* объем. Такие упражнения способствуют формированию понятия переменной величины и функциональной зависимости. (но не готовят не готовят к построению графиков выполняемых на корд плоскости). В 6.кл они знакомятся со столбчатыми диаграммами (от них проще перейти к координатной системе).

2) 7-11 кл – систематическое изучение функции. В 7 кл. изучаются выражения, содержащие переменную (Заполнить таблицу, вычислив значения выражений 3х-1 и -3х+1 для указанных значений х). Учащиеся должны уметь построить график по таблице, найти значение одной переменной величины, если задано значение другой, читать график

На конкретных примерах вводится понятие «функция», «аргумент», «область определения, значений», «график». Введенные функц. понятия получают свою конкретизацию при изучении линейной и квадратичной функции.

Существуют различные подходы к определению ф-ии: Алгебра Киселев: функция определяется как зависимая переменная величина, но в определении отсутствует св-во однозначности ф-ии; Кочетвова: не ясно что такое функция: соответствие между переменными величинами или способ, которым задается это соответствие или переменная величина.

1. На конкретных примерах вводится понятие: аргумент, D(f), E(f), график. Функция трактуется как зависимость одной переменой величины от другой. Учащиеся получают конкретизацию всех этих понятий при изучение линейной функции и её частного вида прямой пропорциональности. Даётся первое представление о способах задания f. Формирование всех понятий сопровождается рассмотрением реальных зависимостей между величинами.

Пр.1: Периметр квадрата зависит от длины его стороны. Пусть сторона квадрата b см., а периметр P. Для каждого значения переменой b можно найти соотв-е значение P. Если b=2, то P=8. Если b=30 , то P=120. Эта зависимость выражается формулой P=4*b,b>0.

Опр: Переменную b, значение которой выбирается произвольно называется независимой переменной. Опр: P, значение которого определяется выбранным значением B, называется зависимой переменной.

В рассмотренном примере каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называют функциональной зависимостью или функцией.

Незав. п.-аргумент. Завис. п. – ф-кция. P квадрата –ф-ция от длины его стороны.

Значение завис. п. = значению функции. Все значения, которые принимает незав. п. величина, образует область определения функции (О.О.Ф).

2. Далее необходимо проводить работу по формированию у учащ-ся умения по формуле находить значения f по известным значениям аргумента (то же задание решать по графику).

Можно построить объяснение иначе:

На доске три задачи.

№1. Поезд движется со За x часов поезд пройдёт расстояниеy км.

Выразите формулой зависимость расстояния от времени. y=60*x.

X	0	1	1.5	…
Y

№2. Длина стороны квадрата x см. Площадь – y. Выразите формулой зависимость площади кв. от его стороны.

X	0	1	1.5	…
Y

№3. Длина ребра куба x см. Объём - . Напишите формулу, которая задаёт зависимость y от x.

X	0	1	1.5	…
Y

Вывод: В каждой задаче рассмат-сь зависимость между переменными x и y. Расстояние, пройденное поездом зависит от времени движения. Площадь кв. зависит от длины его стороны. Объём куба – от его ребра. Обратите внимание на таблицы: каждому значению x соответствует единичное значение y. Зависимости, рассмотренные в задачах, есть функции.

Вопросы: Является ли зависимость, заданная таблицей, функцией?

X	-2	-1	0	1
Y	4	2	0	3

Д./з.: Следует включить упражнения типа:

1. Пешеход идёт со 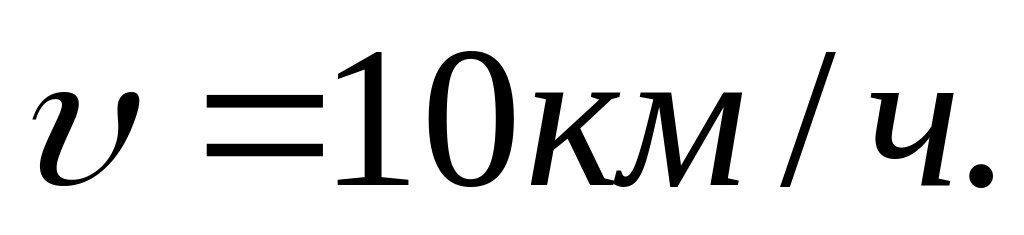Какое расстояние он пройдёт за 3 ч., 6 ч., …..

2. Найти площадь квадрата, если его сторона = …..

3. Найти объём куба, если его ребро = ……

Решение задач записывать в таблицу. При проверке Д./ з. следует подчеркнуть: заданному значению одной величины соотв-т единственное значение другой.

Учащиеся должны понимать, что такое функция, смысл независимой переменной, зависимой, значения функции. Уметь составить формулу, задающую зависимость между аргументами и завис переменной, находить значение завис переменной по заданному значению аргумента.

23. Методика изучения линейной и квадратичной функции.

В школе изучение функциональной зависимости начинается с 1-6 кл. – периода пропидевтики. В этот период не водится определение функции, но на конкретном материале, всеми доступными средствами следует формировать идею функциональной зависимости. Этому способствует решение арифметических задач с переменными данными, заполнение таблиц, построение простейших графиков. При решении текстовых задач следует обращать внимание, на функциональные зависимости, которые лежат в основе (например, зависимость между расстоянием, временем и скоростью). Такая пропидевтика позволяет понять, что есть величины, которые могут менять свое значение. С 5 кл. следует готовить учащихся к построению и чтению графиков. В 6.кл они знакомятся со столбчатыми диаграммами (от них проще перейти к координатной системе).

В 7 кл. изучаются выражения, содержащие переменную (Заполнить таблицу, вычислив значения выражений 3х-1 и -3х+1 для указанных значений х). На конкретных примерах вводится понятие «функция», «аргумент», «область определения, значений», «график».

Введенные функц. понятия получают свою конкретизацию при изучении линейной и квадратичной функции.

Линейная функция.

Осн. цель – ознакомить учащихся с основными функциональными понятиями и с графиками функций: у=кх+b; у=кх. Сформировать представление о числовой функции на примере линейной функции (см. программу).

Изучению линейной ф-ии предшествует изучению ф-ии у=кх и ее графика.

Учащиеся должны понимать, как влияет знак коэфф. к на расположение в координатной плоскости графика функции у=кх, где к≠0, как зависит от значения к и b взаимное расположение графиков двух функций вида у=кх+b.

Начинается работа по формированию у учащихся умений находить значения ф-ии, заданной формулой, графиком, по известному значению аргмента; по графику ф-ии определять значение аргумента, если значение ф-ии задано.

Обычно рассмотрение лин. ф-ии начинается с задачи на равномерное прямолинейное движение, а иногда с построения графика некоторой лин. ф-ии. Лучше использовать первый способ.

Рассмотрим примеры функций.

Пример1. На шоссе расположены пункты А и В, удаленные друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном А, со скоростью 50 км/ч. За t ч. Мотоциклист проедет 50 t км и будет находиться от А на расстоянии 50 t+20 км. Если обозначить буквой s расстояние мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой s=50 t+20 , где t≥0.

Пример 2. Ученик купил тетради по 3 к. за штуку и ручку за 35 к. Стоимость покупки зависит от числа тетрадей. Обозначим число купленных тетрадей буквой х, а стоимость покупки у. Получим: у=3х+35, где х - натуральное число.

В этих примерах мы встретились с функциями, заданными формулами вида у=кх+b, где х - независимая переменная, к и b – числа. Такие функции называются линейными.

Линейной функцией называется функция, которую можно задать формулой вида у=кх+b, х- независимая переменная, к и b- некоторые числа.

Построим график линейной ф-ии у=0,5х-2. Составим таблицу соответственных значений х и у:

х	-6	-4	-2	0	2	4	6	8
у	-5	-4	-3	-2	-1	0	1	2

Отметим в корд. плоскости полученные точки. Все отмеченные точки лежат на одной прямой. Эта прямая является графиком ф-ии у=0,5х-2.

Вообще, графиком линейной ф-ии явл. прямая. Для построения графика лин ф-ии достаточно найти координаты двух точек графика, отметить эти точки в корд. плоскости и провести через них прямую.

Пример3 Построим график ф-ии у=2х+3. Эта ф-ия линейная, поэтому графиком ее явл прямая. Используя формулу у=2х+3, найдем корд двух точек графика:

Если х=-2, то у= -1, х=1, то у=5. Отметим точки А(-2;-1) и В(1;5). Проведем через эти точки прямую. Прямая АВ есть график ф-ии у=2х+3.

При построении графика линейной ф-ии часто бывает удобно в качестве одной из точек брать точку с абсциссой 0.

При к=0 формула у=кх+b имеет вид у=0х+b т.е у=b, принимает одно и тоже значение при любом х.

Пример5. Построим график ф-ии у= -2. Любому значению х соответствует одно и тоже значение у, равное -2. Отметим две какие-нибудь точки с ординатой -2, например Р(0;-2) и N(4;-2), и проведем через них прямую. Прямая РN- график лин ф-ии у= -2.

Если область определения лин. ф-ии состоит не из всех чисел, то ее график представляет собой соответствующую часть прямой (полупрямая, отрезок).

Система контроля (любые примеры).

При построении используется метод сгущения точек:

а) нанесение нескольких точек

б) наблюдение: все построенные точки располагаются на одной прямой

в) проверка: берем произвольное значение аргумента, вычисляем соответствующее значение ф-ии, наносим точку на координатную плоскость, показываем, что она принадлежит построенной прямой. Отсюда делается вывод о графике данной линейной ф-ии.

Пример 6. Пусть V – объем железного бруска, m-его масса. Т.к. плотность железа равна 7,8 г/см³, то m=7,8V. Зависимость массы железного бруска от его объема является примером ф-ии, которая задается формулой вида у=кх, где х - независимая переменная, к – число, отличное от нуля. Такую ф-ию называют прямой пропорциональностью.

Определение. Прямой пропорциональностью называется ф-ия, которую можно задать формулой вида у=кх, где х-нез. переменная, к- неравное нулю число. Явл частным случаем лин ф-ии, при b=0. Графиком явл прямая, проходящая через начало координат. Засположение графика зависит от коэфф. к.

Квадратичная ф-ия.

Осн. цель – выработать умение строить график квадратичной ф-ии и применять графические представления для решения неравенств второй степени с одной переменной.

Изложение темы начинается с систематизации сведений о ф –ях. Рассматриваются св-ва ранее изученных функций: у=кх+b; у=к/х. Подготовкой может служить рассмотрение св-в ф-ии у=х². Изучению кв. ф-ии предшествует рассмотрение вопроса о кв. трехчлене и его корнях, разложении кв. трехчлена на множители.

Изучение кв. ф-ии начинается с рассмотрения ф-ии у=х²,, у=ах², ее св-в и особенностей графика, а также др. частных видов кв. ф-ии (у= ах²+b, у=а(х-m) ², у=х²+рх+q).

Приемы построения графика ф-ии у= ах²+bх+с обрабатываются на конкретных примерах (по точкам). Следует уделять внимание формированию у учащихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы. Дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания ф-ии. Формирование умений решать нер-ва вида ах²+bх+с>0 и ах²+bх+с<0 где а≠0,осуществляется с опорой на сведения о графике кв. ф-ии.

В 7 кл в теме «степень с нат показателем» рассматривается ф-ия у=х². Учителю необходимо подчеркнуть: св-ва этой ф-ии во многом отличаются от св-в лин ф-ии. Эта ф-ия не монотонна. Дать учащимся упражнение: ф-ия у= х² задана на промежутке -2≤х≤3. Найти множество значений этой ф-ии. Ученики, как правило, дают ответ 4≤у≤9, что неверно. Ошибка в переносе св-ва монотонности лин ф-ии на квадратичную. Эта ошибка требует тщательного рассмотрения графика ф-ии у= х². Другая особенность этой ф-ии в том, что характер изменения значений ф-ии не равномерный. На одном участке она растет быстрее, на другом медленнее. Эта особенность выявляется при рассмотрении графика. Целесообразно рассматривать два одинаковых графика в крупном масштабе на промежутке -1≤х≤1, другой в мелком на -3≤х≤3. Построение вести методом загущения. Важно отметить св-во параболы –симметричность относительно оси ординат(в дальнейшем это св-во приведет к рассмотрению класса четных ф-ий).

Квадратичной ф-ей называется ф-ия, которую можно задать формулой вида у=ах²+bх+с, где х-независимая переменная, а, b,с – некоторые числа, причем а≠0.

Примером кв ф-ии явл зависимость пути от времени при равноускоренном движении. Если тело движется с ускорением а м/с² и к началу отсчета времени t прошло путь s м, имея в этот момент скорость v м/c, то зависимость пройденного пути s от времени t выражается формулой

S=

Если, например, а=6, v =5, s =20, то формула примет вид: S=3t² +5t+20.

Изучения квадратичной ф-ии начинается с частного случая - ф-ии у= ах². При а=1, получаем у= х² с которой уже встречались ранее. Ее графиком явл парабола.

Построим график ф-ии у=2х² (составляется таблица(10 значений), по ней отмечаются точки, соединяются плавной линией, получаем график необходимой ф-ии) Этот график сравнивается с графиком ф-ии у=х² (соотв значения в 2 раза больше; растяжение у=х² от оси х в 2 раза). Далее строится график у=1/2 х² и делаются аналогичные выводы (сжатие у=х² к оси х в 2 раза). Делается обобщение для а>1 и для 0<а<1.

Строится график ф-ии у=-1/2 х² .Он сравнивается с у=1/2 х² и делается вывод о получении графика с помощью симметрии относительно оси х.

Формулируются св-ва графика у= ах² при а>0 и а<0 (проходят через нач корд; расположение в полуплоскостях; симметричность относит оси у; промежутки убыв и возр; наиб и наим значения) Делаются выводы о направлении ветвей параболы, в зависимости от а. Дается определение вершины (точка пересечения параболы с ее осью симметрии).

Далее рассматриваются другие частные случаи кв ф-ии: у= ах²+b, у=а(х-m) ², и на конкретных примерах показывается как получить данные графики из графика ф-ии у=ах² (преобразование графиков).

Далее выводятся формулы для нахождения вершины параболы m= - , n= , осью симметрии служит прямая у=m, параллельная оси у. Дается алгоритм построения графика кв ф-ии:

1) Найти корд вершины и отметить ее в корд пл-ти

2) Построить еще несколько точек, принадлежащих параболе

3) соединить отмеченные точки плавной линией

Обязательно наличие шаблонов графиков различных ф-й в зависимости от а. У учителя большие, у учеников маленькие из картона.