Умножение дес дробей на нат числа
рассматривается задача: пусть поле имеет форму квадрата со стороной 1,83 км. Найдем периметр этого поля. Он равен 1,83+1,83+1,83+1,83=7,32 км. Это сумма четырех слагаемых, равных 1,83. Ее называют произведением числа 1,83 на нат число 4. Обозначают 1,83*4
Произведением дес дроби и нат числа называют сумму слагаемых, каждое из которых равно этой дроби, а количество слагаемых равно этому нат числу
Умножить 1,83 на 4 можно было не обращая внимание, на запятую, а в полученном произведении 732 отделить запятой 2 цифры справа, т.е столько, сколько цифр в дроби 1,83 (Записать столбиком) 1,83*4=7,32
Деление дес дробей на нат числа
можно ввести также рассматривая задачу: кусок ленты, длиной 19, 2 м разделили на 8 частей. Найдите длину каждой части. Для решения выразим длину ленты в дм, т.е 19,2 м =192 дм. Но 192:8=24. Значит длина каждой части 24 дм => 2,4 м.
Тот же ответ можно получить, не переводя метры в дм. Надо разделить 19,2 на 8, не обращая внимание на запятую и поставить в частном запятую, когда кончится деление целой части (разделить столбиком). Если целая часть меньше делителя, то частное начинается с нуля целых. Например, 2,88:4=0,72.
Умножение десятичных дробей
Чтобы умножить 4,6 на 0,3, надо сначала 4,6 умножить на 3, а потом результат поделить на 10. Тот же результат получим, если умножить 4,6 на 0,3, не обращая внимание на запятые, а в полученном произведении отделить запятой 2 цифры справа, т. е столько цифр, столько их стоит после запятой в обоих множителях вместе.
Если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
Деление на дес дробь. Рассмотрим задачу: площадь прямоугольника равна 2,88 кв дм, а его ширина 0,8 дм. Чему равна длина прямоугольника.
Т.к 2,88 кв дм =288 кв см; 0,8 дм =8 см => длина прямоугольника равна 288:8, т.е 36 см=3,6 дм. Тот же ответ можно получить, не переводя дм в см. Для этого надо умножить делитель 0,8 и делимое 2,88 на 10 (перенести в них запятую на одну цифру вправо) и разделить 28,8 на 8. Снова получим 28,8:8=3,6
Чтобы разделить число на дес дробь, надо: 1)в делимом и делителе перенести запятую вправо на столоько цифр, сколько их после запятой в делителе. 2)после этого выполнить деление на нат число
Дать упражнения для закрепления материала, задачи, решаются умножением (делением) дес дробей; простейшие уравнения с простейшими дробями.
16. Методика ввеления отрицательных чисел.
В 6 классе: 1) Положительные и отрицательные числа. Основная цель – расширить представления учащихся о числе путем введения отрицательных чисел. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой, с тем чтобы она могла служить наглядной основой для правил сравнения чисел, , сложения и вычитания чисел, рассматриваемых в следующей теме. Особое внимание следует уделить изучению понятия модуля числа. 2) Сложение и вычитание положительных и отрицательных чисел. Основная цель – выработать прочные навыки сложения и вычитания положительных и отрицательных чисел (вспомнить действия с целыми и дробными числами). 3) Умножение и деление положительных и отрицательных чисел. Основная цель – выработать прочные навыки арифметических действий с положительными и отрицательными числами. При изучении данной темы учащиеся должны усвоить, что для обращения обык. Дроби в десят. Достаточно разделить числитель на знаменатель.
Историческая справка. Раздел положительные и отрицательные числа являются одним из самых трудных в методическом отношении. До введения отрицательных чисел учащиеся были знакомы с целыми и дробными положительными числами и нулем, поэтому не было надобности в термине положительные числа. После того как они познакомились с числами другого вида, с отрицательными, вводится новое название положительные и отрицательные числа. Для обозначения совокупности всех этих чисел в методической литературе встречаются два названия: «рациональные» числа, «относительные» числа. Термин «относительные» числа существуют во многих странах, во многих учебниках. Из отечественных школьных учебников термин убрали. Добавилось такое определение (числа положительные, отрицательные и ноль называются относительными числами в отличии от чисел обыкновенных или арифметических, которые не имеют перед собой никакого знака). Введение термина относительные числа приводят к неверному представлению о существовании чисел лишенных знака.
Введению отрицательных чисел следует предпослать небольшой исторический обзор развития понятия числа. Напомнив учащимся, что первыми числами, с которыми они познакомились – натуральные числа и ноль. Натуральные числа возникли в связи с потребностью подсчета конкретных предметов. Само понятие натурального числа оформилось в процессе таких подсчетов. Действия вычитания и деление, которые определяются через сложение и умножение не всегда выполнимы во множестве натуральных чисел и нуля. Важно подчеркнуть, что невозможность выполнения обратных арифметических действий во множестве натуральных чисел и нуля связано, с невозможностью выразить результаты соответствующих жизненных задач. Первым обобщением натуральных чисел были дробные числа, возникшие с потребностью измерения какой-либо величины, все дальнейшее расширение понятия числа уже не были связаны с потребностями счета или измерениями, а являлись следствием развития науки. Первыми из них было введение отрицательных чисел, обусловленное развитием алгебры. При решении уравнений возникла необходимость из меньшего числа вычитать большее.
Индийские математики, стараясь найти образцы такого вычитания, пришли к его толкованию с точки зрения торговых расчетов. В Европе отрицательные числа были введены Рене Декартом в 1637 г., когда вышла работа «Геометрия».
Различные подходы к введению понятия отрицательных чисел. В учебной и методической литературе используются различные способы введения отрицательных чисел: 1) формально-логический: введение отрицательных чисел объясняется выполнением действия вычитания во всех случаях; 2) реально-конкретный: он исходит из непосредственной связи с действительностью, с конкретными представлениями. В школьном курсе математики сочетаются реально-конкретный и формально-логический пути. Для нового понятия отрицательного числа надо не только дать определение, но и необходимо определить понятие равенства, определить понятие больше, меньше, указать критерий сравнения новых чисел между собой и с ранее известными. Определить действия сложение, вычитание, умножение и деление, показать, что законы действий установленные для ранее изученной, справедливы для новых чисел.
Изучение темы в 6 классе. Учащиеся должны хорошо знать смысл и значение отрицательных чисел, поэтому введение их должно быть мотивировано: а) мотивом может быть возможность выполнения вычитания (алгебраическое); б) геометрический (соответствие между точками прямой и числами); в) практической (характеристика измерения величин). В школьном курсе отрицательные числа вводятся на наглядной геометрической основе, как способ обозначения положения точки на прямой относительно начала отсчета. Целесообразно показать, что известных чисел недостаточно для характеристики положения точки на прямой по отношению к началу отсчета.
Задача: Поезд вышел со станции Кострома и идет со скоростью 90км/ч. В какой город или в какое место приедет поезд через три часа? Чтобы определить положение точки на прямой по отношению к началу отсчета, недостаточно указать расстояние от начало отсчета. Надо указать по какую сторону от начало отсчета точка находится.
Тема урока: «Координаты на прямой». Начертите на доске вместе со мной прямую, отметьте точку О.
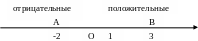
Выберем единичный отрезок и примем точку О за начало отсчета. Точка О разбивает прямую на два дополнительных луча. Положение точки на прямой на каждом из лучей задается ее координатами. Чтобы отличить, друг от друга координаты на этих лучах условились ставить перед координатой одного луча «+», а другой – «-». Число +1 называется положительным, -1 – отрицательным, 0 – начало отсчета. Прямая, с выбранными на ней единичными отрезками называется координатной прямой. Число, показывающее положение точки на прямой называется координатой точки А. –2 координата точки А. Контроль за усвоением: 1) Справа или слева от начала отсчета находятся точки А(-8), В(100). Какая из них находится ближе к началу отсчета? 2) Запишите координату точки О. 3) Запишите координату точки, лежащей правее точки А(-8) на единицу. 4) Запишите координату точки С, лежащей левее точки В на 2 единицы. 5) Начертите координатную прямую и отметьте на ней точки: А(5), В(1), С(-1), Д(-3).
Тема урока: «Сложение и вычитание положительных и отрицательных чисел». В методической литературе существуют различные подходы к введению сложения отрицательных чисел: 1) формальный (задачи, решаемые в арифметическим сложение должны решаться теми же действиями, что и с рациональными числами, правила сложения положительных чисел известное в арифметике сохраняются и для сложения рациональных чисел, законы сложения должны сохраняться и для сложения рациональных чисел). Формальный метод труднее, так как учащимся даются с начала правило, а затем все закрепляется на примерах. 2) конкретный. Задача: Самолет находится на некоторой высоте, затем высота самолета изменилась на а м, а потом еще на в м. На сколько метров изменилась высота самолета? 1) а = 500 м, в = 300 м общая 800 м; 2) а = -500 м, в = -300 м общая -800 м. Правило по аналогии.
Действия с отрицательными числами (примеры, с градусником и числовой прямой).
Прибавить к числу а число в – значит изменить число а на в единиц. Чтобы сложить два отрицательных числа, надо: 1) сложить их модули, 2) поставить перед полученным числом знак «-». Чтобы сложить два числа с разными знаками, надо: 1) из большего модуля слагаемых вычесть меньший, 2) поставить перед полученным числом знак того слагаемого, модуль которого больше. Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому. Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак «-». Чтобы перемножить два отрицательных числа, надо перемножить их модули. Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя. При делении чисел с разными знаками, надо: 1) разделить модуль делимого на модуль делителя, 2) поставить перед полученным числом знак «-». Делить на ноль нельзя!