54. Задачи дискретизации (общая постановка)
Сущность дискретизации аналоговых сигналов заключается в том, что непрерывность во времени аналоговой функции s(t) заменяется последовательностью коротких импульсов, амплитудные значения которых cn определяются с помощью весовых функций, либо непосредственно выборками (отсчетами) мгновенных значений сигнала s(t) в моменты времени tn.Представление сигнала s(t) на интервале Т совокупностью дискретных значений cn записывается в виде: (с1, с2, ... , cN) = А[s(t)],
где А - оператор дискретизации. Запись операции восстановления сигнала s(t): s'(t) = В[(с1, с2, ... , cN)].
Выбор операторов А и В определяется требуемой точностью восстановления сигнала. Числовая информация, как и символьная, по своей природе дискретна, так как она может быть представлена ограниченным набором символов (в частности, цифр).
На рис. 2.4 показана дискретизация непрерывной зависимости U(t). Она включает две составляющих:
-дискретизацию по времени с шагом ∆t;
-дискретизацию (квантование) по уровню с шагом ∆U.
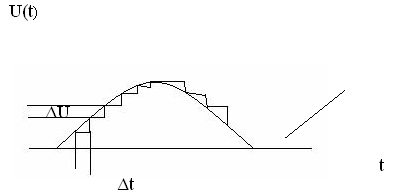
Рис.2.4. Дискретизация непрерывного сигнала
Благодаря этим двум этапам всю зависимость U(t) можно представить как последовательность дискретных значений, которым соответствуют числа.
Очевидно, что точность дискретизации по уровню может быть выбрана как угодно большой
Важно, что непрерывную информацию с помощью оцифровки (дискретизации) принципиально в любом случае можно представить, как дискретную с любой необходимой точностью. В то же время, обратное преобразование иногда невозможно (например, для символов). Таким образом, дискретная форма представления информации является наиболее общей.
В соответствие с формами представления информации выделяют и типы дискретных, и непрерывных сообщений. Первые состоят из знаков, принадлежащих к определенному алфавиту. Вторые включают непрерывно меняющиеся во времени величины.
Принципиально важно, что непрерывная информация в любом случае может быть преобразована к дискретной, тогда как обратное преобразование возможно не всегда.
Действительно, непрерывную зависимость некоторых величин можно дискретизировать, если задавать их соответствие в ограниченном наборе точек. При этом точность такого преобразования принципиально может быть задана достаточно высокой, чтобы не потерять информацию. А вот однозначно восстановить неизвестную кривую по ограниченному набору точек возможно не всегда.
55. Геометрическая интерпретация блоковых корректирующих кодов.
Линейным блоковым (n,k) - кодом называется множество N последовательностей длины n над GF(q), называемых кодовыми словами, которое характеризуется тем, что сумма двух кодовых слов является кодовым словом, а произведение любого кодового слова на элемент поля также является кодовым словом.
Обычно N=qk , где k - некоторое целое число.
Если q=2, линейные коды называются групповыми, так как кодовые слова образуют математическую структуру, называемую группой. При формирование этого кода линейной операцией является суммирование по mod2.
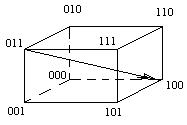
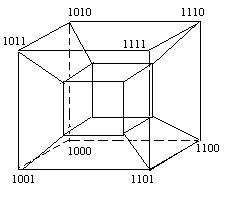
Любая n – разрядная КК(кодовая комбинация?) может быть представлена как вершина n – мерного единичного куба, длин ребра =1
