31. Дискретизация и принципы восстановления информации.

Поскольку реальные сигналы всегда изменяются во времени плавно, их можно передавать по линии связи в виде последовательности отсчетов. Преимущества такого способа передачи мы рассмотрим поз; а сейчас выясним, каким образом выбирать шаг дискретизации Δt. Чем больше величина Δt, тем меньше информации нужно передавать по каналу. Вместе с тем выбор должен быть таким, чтобы исходный сигнал можно было без потерь информации восстановить по дискретным отсчетам. Выбор шага Δt и соответствующей ему частоты дискретизации f_d=1/Δt определяется теоремой Котельникова-Найквиста, согласно которой:

Любой сигнал U(t), не содержащий частот выше f_m можно точно восстановить по его отсчетам U(kAt) , взятым с частотой f_d=2f_m

В теореме доказывается, что точное восстановление сигнала возможно с помощью ряда

где слагаемые представляют из себя функции Котельникова, амплитуда которых U(k∆t) соответствует амплитудам отсчетов, а форма показана на рис.25.1. Сигнал такого вида можно получить, если подать прямоугольные импульсы на вход идеального фильтра низких частот с граничной частотой f_m. Поскольку реальные ФНЧ отличаются от идеальных, частоту дискретизации принимают с определенным запасом. Так, в телефонах, где в качестве f_m принимается экспериментально определенная граничная частота «слоговой разборчивости» речи 3,4 кГц, частоту дискретизации выбирают равной не 2*3,4=6,8 кГц, а 8 кГц.

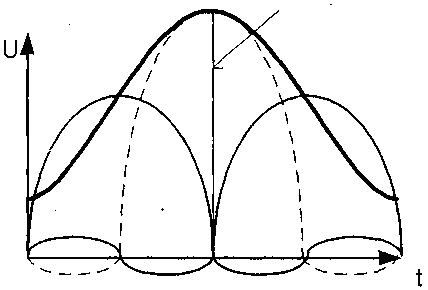
Рис.25.1 Восстановление исходного сигнала как суммы значений функций Котельникова для разных отсчетов.

32. Разность модуляции и приема.

Амплитудная модуляция (amplitude modulation, АМ) исторически была первым видом модуляции, освоенным на практике. В настоящее время АМ применяется в основном только для радиовещания на сравнительно низких частотах (не выше коротких волн) и для передачи изображения в телевизионном вещании. Это обусловлено низким КПД использования энергии модулированных сигналов.

АМ соответствует переносу информации s(t)  U(t) при постоянных значениях параметров несущей частоты ω и ψ. АМ – сигнал представляет собой произведение информационной огибающей U(t) и гармонического колебания ее заполнения с более высокими частотами. Форма записи амплитудно-модулированного сигнала:

u(t) = U(t)cos(ω_ot+ψ _o), (1.1)

U(t) = U_m[1+Ms(t)], (1.2)

где U_m – постоянная амплитуда несущего колебания при отсутствии входного (модулирующего) сигнала s(t), М – коэффициент амплитудной модуляции

Значение М характеризует глубину амплитудной модуляции. В простейшем случае, если модулирующий сигнал представлен одночастотным гармоническим колебанием с амплитудой S_o, то коэффициент модуляции равен отношению амплитуд модулирующего и несущего колебания М=S_o/U_m. Значение М должно находиться в пределах от 0 до 1 для всех гармоник модулирующего сигнала. При значении М<1 форма огибающей несущего колебания полностью повторяет форму модулирующего сигнала s(t), что можно видеть на рис. 1.1 (сигнал s(t) = sin(ω_st)). Малую глубину модуляции для основных гармоник модулирующего сигнала (М<<1) применять нецелесообразно, т.к. при этом мощность передаваемого информационного сигнала будет много меньше мощности несущего колебания, и мощность передатчика используется неэкономично.

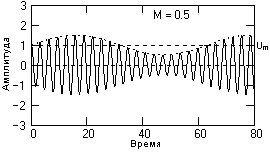
Модулированный сигнал

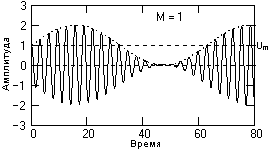
глубокая модуляция