
- •Содержание.
- •3 Задания типового расчёта №2__________________________________22
- •1. Требования к оформлению типового расчёта
- •Типовой расчёт №1
- •II семестр
- •2. Задания типового расчёта №1
- •Задание №1.
- •Задание №2.
- •Задание №3.
- •Задание №4.
- •Задание № 5.
- •Задание №6.
- •Задание №7.
- •Задание №8.
- •3. Задания типового расчёта №2
- •Задание №1
- •Задание №2.
- •Задание №3.
- •Задание №4
- •З адание №5.
- •Задание №6.
- •Задание №8.
- •Задание №9.
- •Задание №10.
- •Задание №11.
- •Задание №12.
- •4. Примерный список рекомендуемой литературы
3. Задания типового расчёта №2
Темы:
«Элементы матричного анализа»
«Элементы векторной алгебры»
«Аналитическая геометрия в пространстве и на плоскости»
Задание №1
Вычислить:
1.1. 2A
+ BC,
если A
=
![]() ;
B
=
;
B
=
![]() ;
С =
;
С =
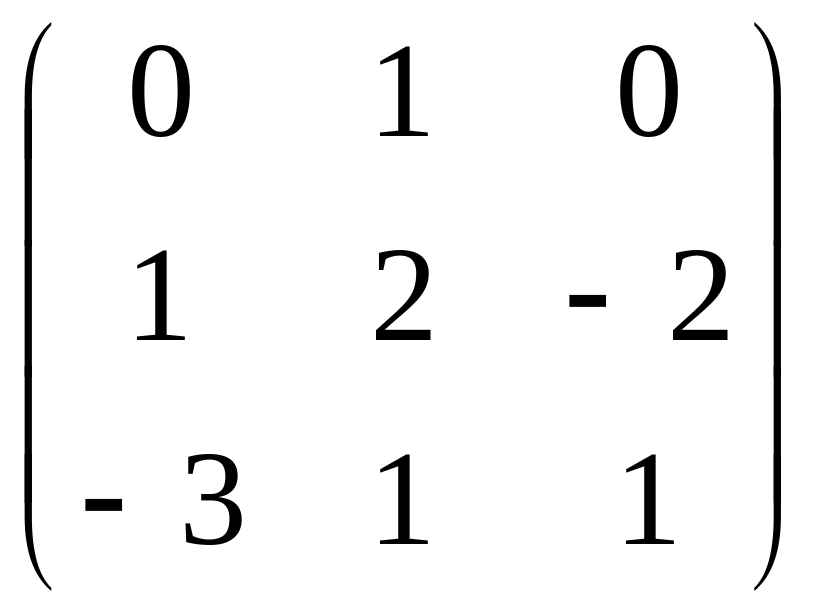 .
.
1.2. 3A –
BC, если
A =
![]() ;
B =
;
B =
![]() ;
С
=
;
С
=
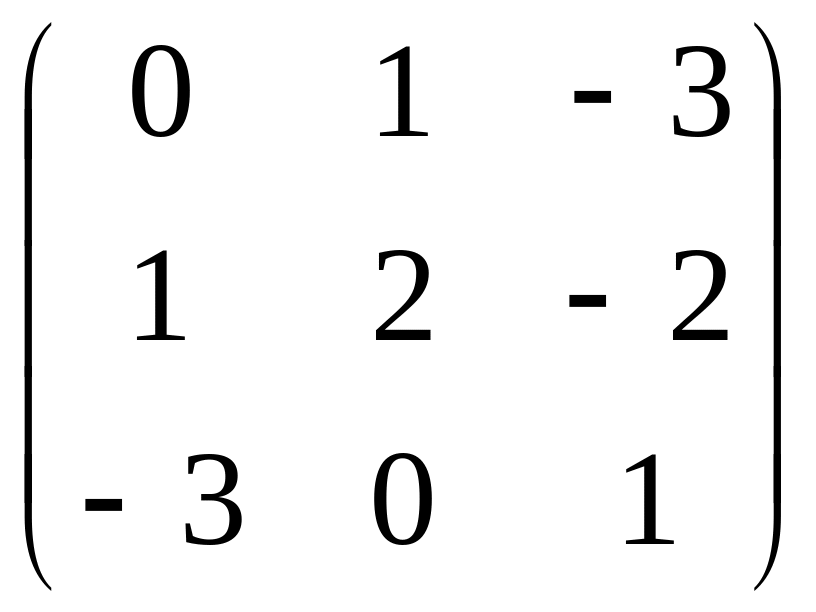
1.3. BC –
4A, если
A =
![]() ;
B =
;
B =
![]() ;
С
=
;
С
=
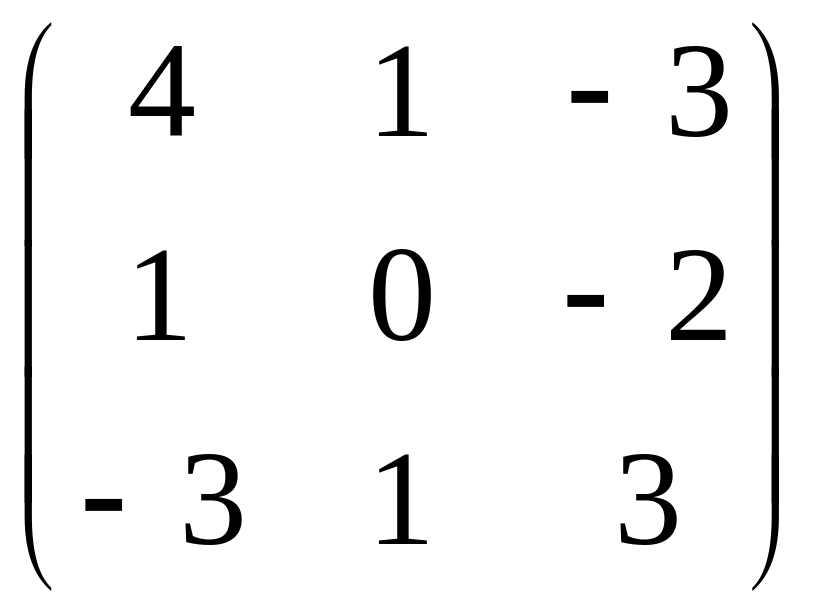 .
.
1.4. 5A
+BC, если
A =
![]() ;
B =
;
B =
![]() ;
С
=
;
С
=
 .
.
1.5. 2AB +
C, если
A =
 ;
B =
;
C =
;
B =
;
C =
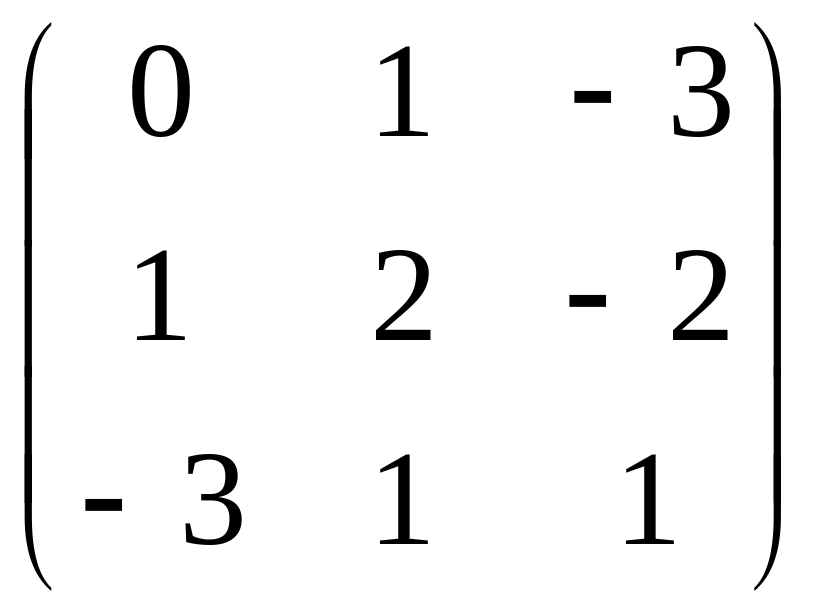 .
.
1.6. AB +
3C, если
A =
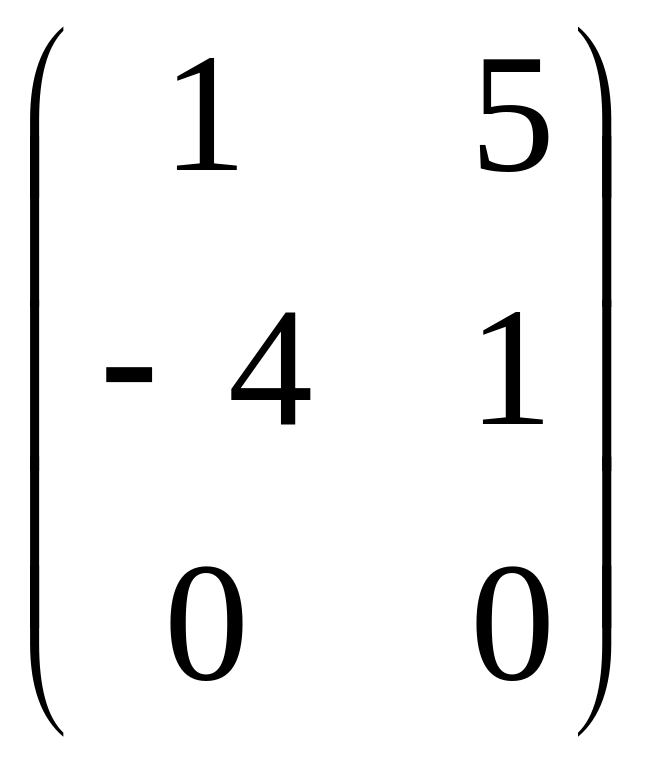 ; B =
; B =
![]() ; C =
; C =
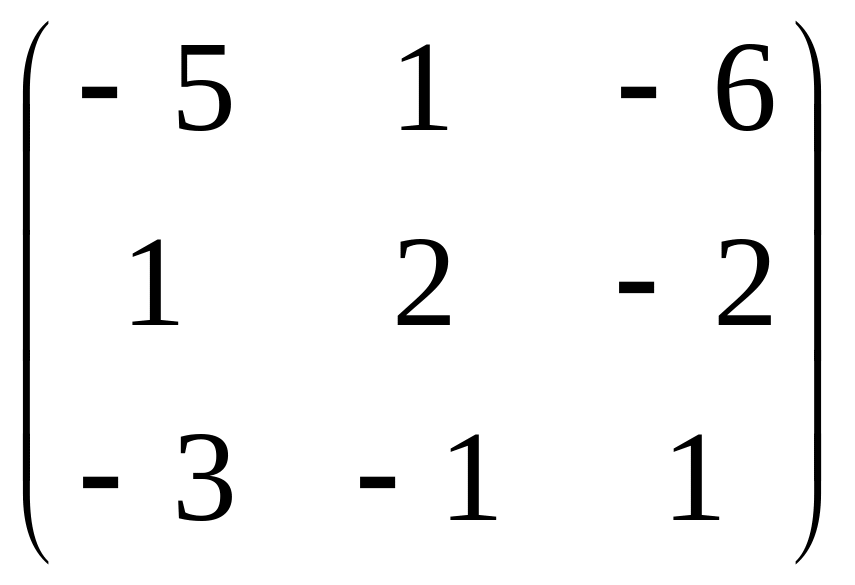 .
.
1.7. AB
– 4C
, если A
=
 ; B
=
; B
=
![]() ; С =
; С =
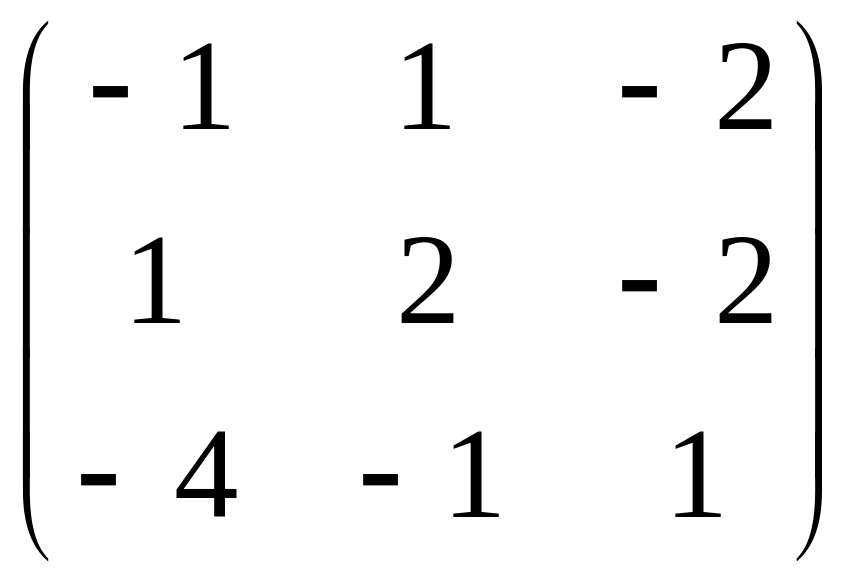 .
.
1.8. AВ
+ 5C,
если A
=
 ; B
=
; B
=
![]() ; C
=
; C
=
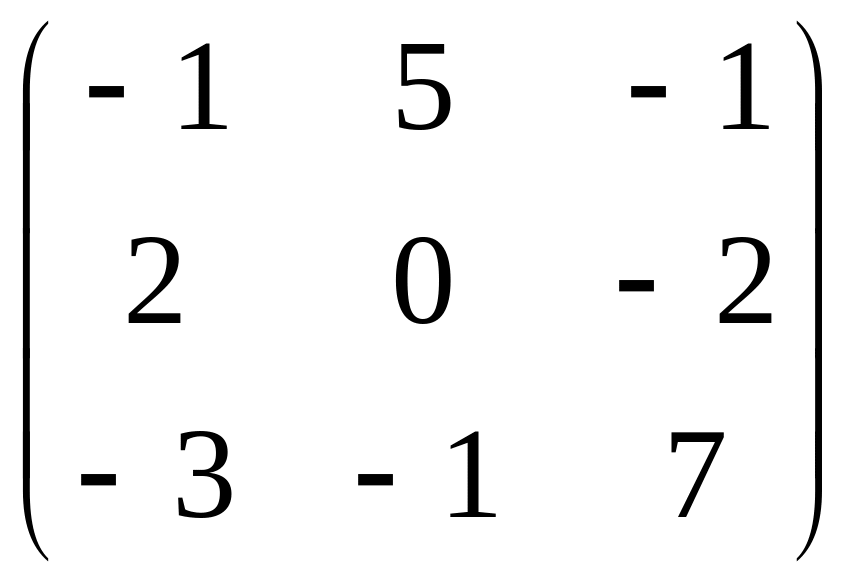 .
.
1.9. AB
+ 3C,
если A
=
![]() ; B
=
; B
=
![]() ; С =
; С =
 .
.
1.10. AB +
2C, если
A =
![]() ; B =
; B =
![]() ; C =
; C =
 .
.
1.11. AB –
4C, если
A =
![]() ; B =
; C =
; B =
; C =
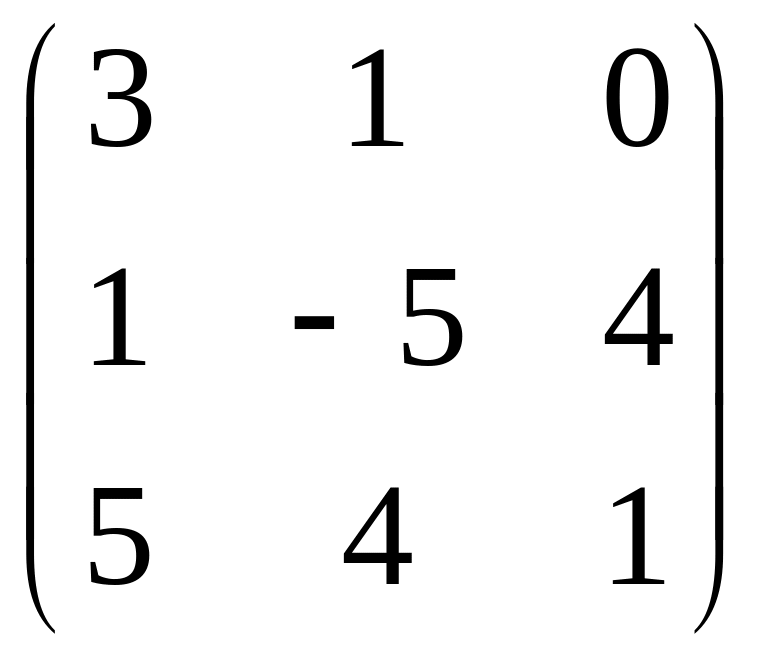 .
.
1.12. AB
– 3C,
если A
=
![]() ; B
=
; B
=
![]() ; С =
; С =
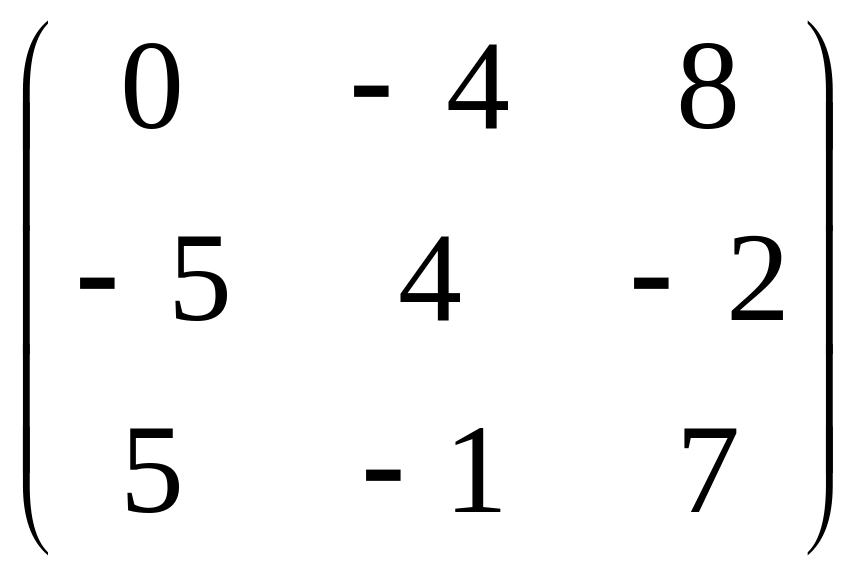 .
.
1.13. 3A +
BC, если
A =
![]() ; B =
; B =
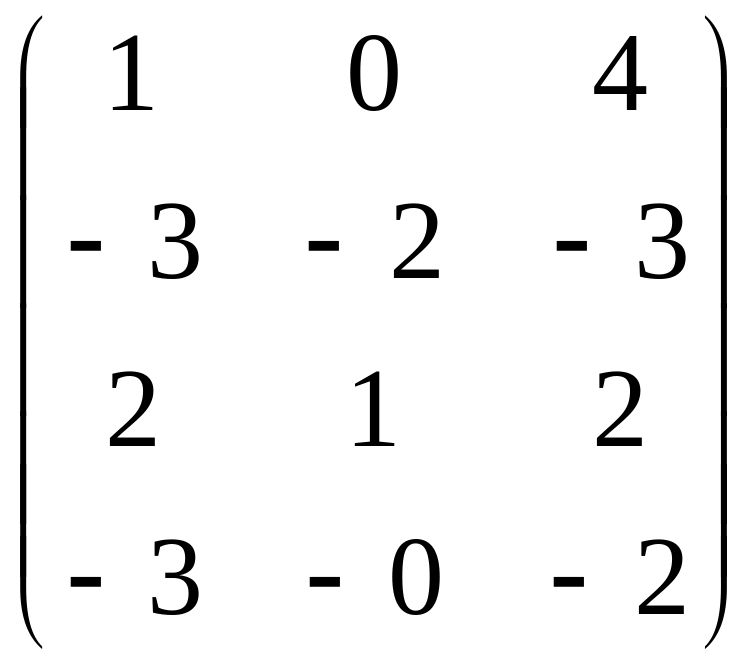 ; C =
.
; C =
.
1.14. 4A
–BC, если
A =
![]() ; B =
; B =
 ; С
=
; С
=
![]() .
.
1.15. A +
2BC, если
A =
![]() ; B =
; B = ; С
=
; С
=
![]() .
.
1.16. A –
2BC, если
A =
 ; B =
; B =
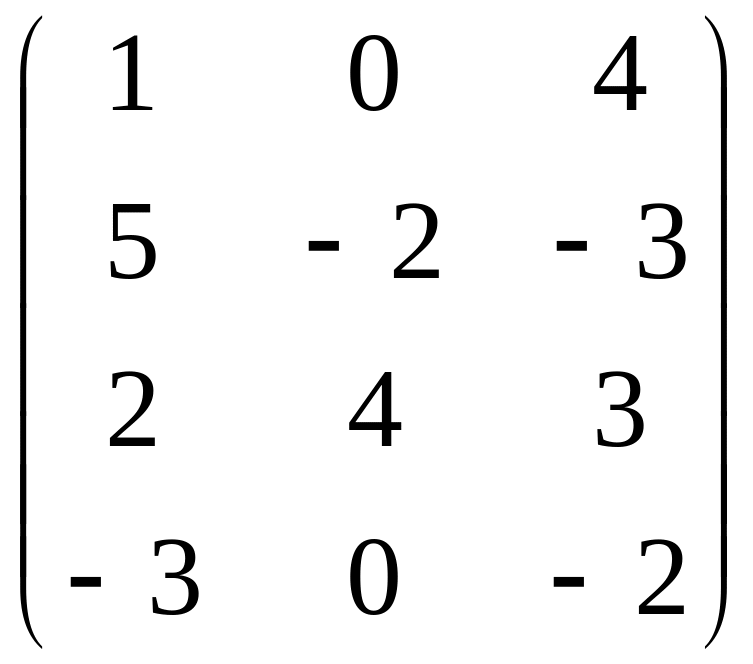 ; С
=
; С
=
![]()
1.17. 2A +
BC, если
A =
![]() ; B =
; B =
![]() ; С
=
; С
=
 .
.
1.18. 3A –
BC, если
A =
![]() ; B =
; B =
![]() ; С
=
; С
=
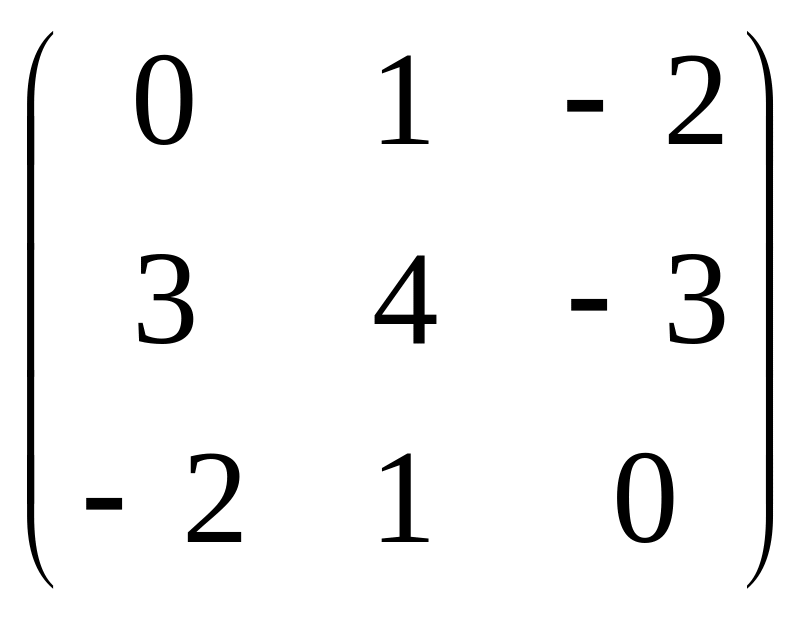 .
.
1.19. BC –
4A, если
A =
![]() ; B =
; B =
![]() ; С
=
; С
=
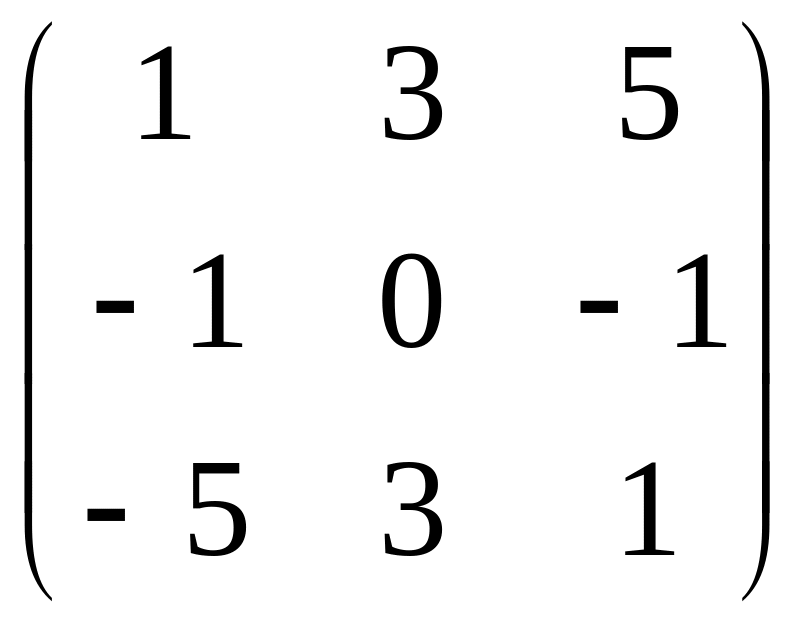
1.20. 5A +
BC, если
A =
![]() ; B =
; B =
![]() ; C =
; C =

1.21. 2AB +
C, если
A =
 ; B =
; B =
![]() ; C =
; C =
 .
.
1.22. AB +
3C, если
A =
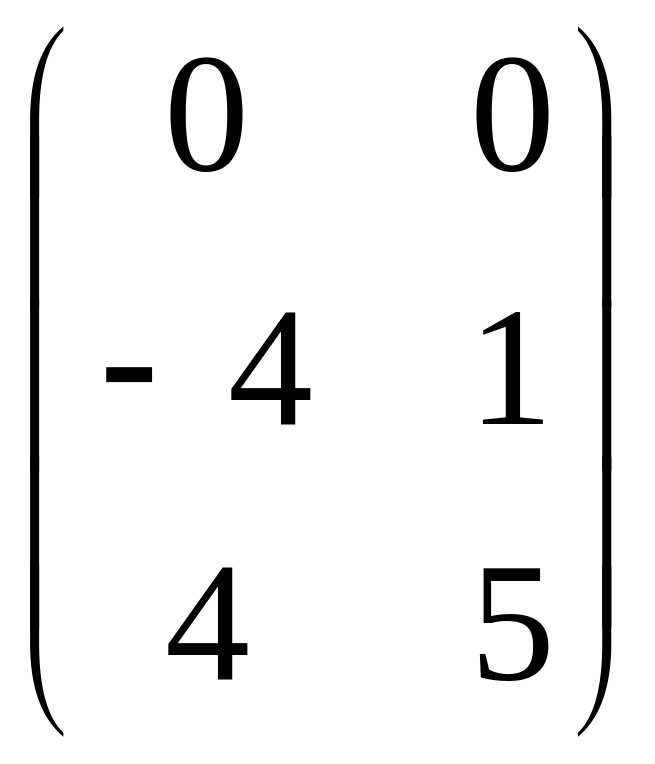 ; B =
; B =
![]() ; C =
; C =
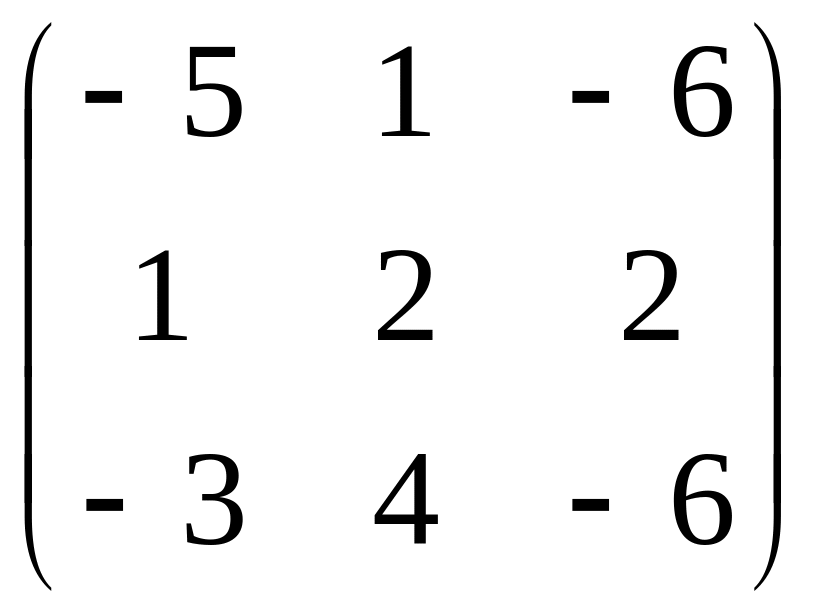 .
.
1.23. AB –
4C, если
A =
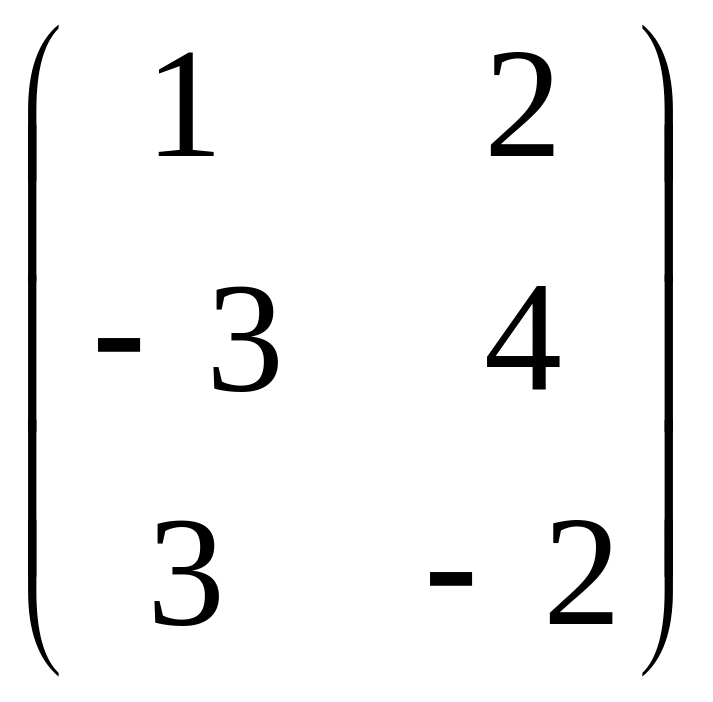 ; B =
; B =
![]() ; C =
; C =
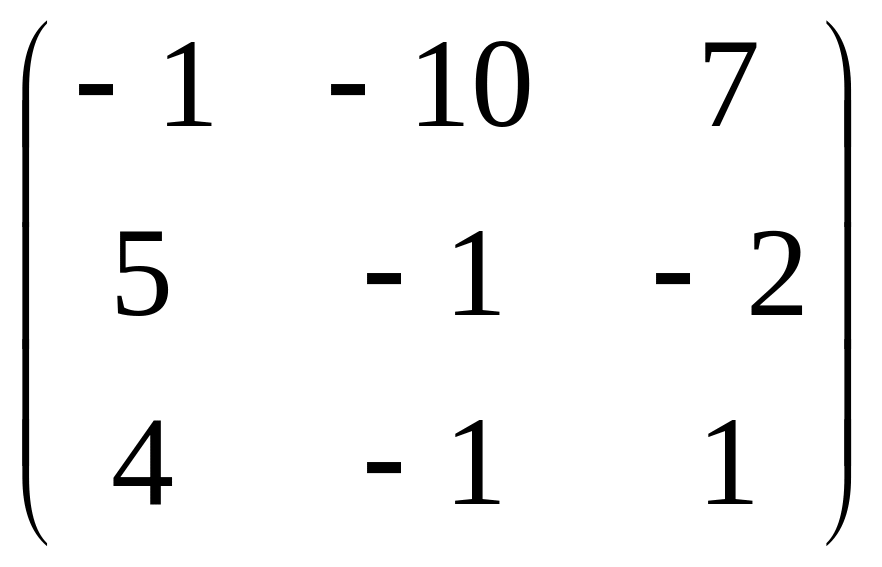 .
.
1.24. AB +
5C, если
A =
 ; B =
; B =
![]() ; C =
; C =
 .
.
1.25. AB
+3C, если
A =
![]() ; B =
; B =
![]() ; C =
; C =
 .
.
1.26. AВ
+ 2C, если
A =
![]() ; B =
; C =
; B =
; C =
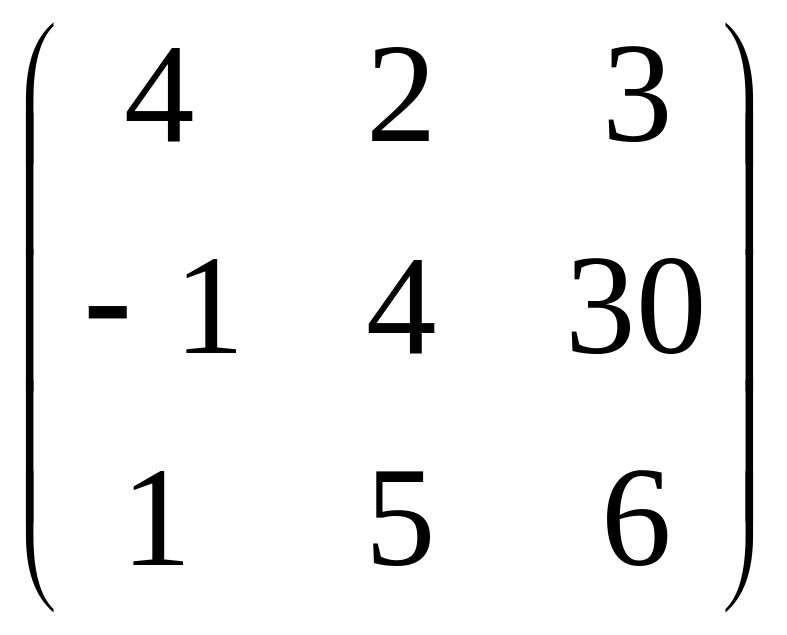 .
.
1.27. AB –
4C, если
A =
; B =
![]() ; C =
; C =
 .
.
1.28. AB –
3C, если
A =
![]() ; B =
; B =
![]() ; C =
; C =
 .
.
1.29. 3A +
BC, если
A =
![]() ; B =
; B =
 ; С
=
.
; С
=
.
1.30. 4A –
BC, если
A =
![]() ; B =
; B =
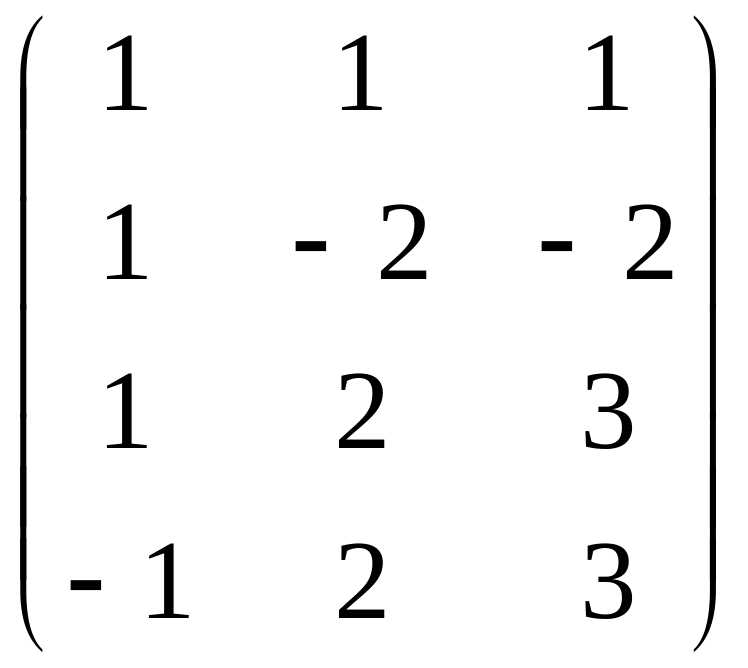 ; С
=
; С
=
![]() .
.
Задание №2.
Вычислить определитель: 1) разложением по элементам столбца; 4) разложением по элементам строки
2.1.
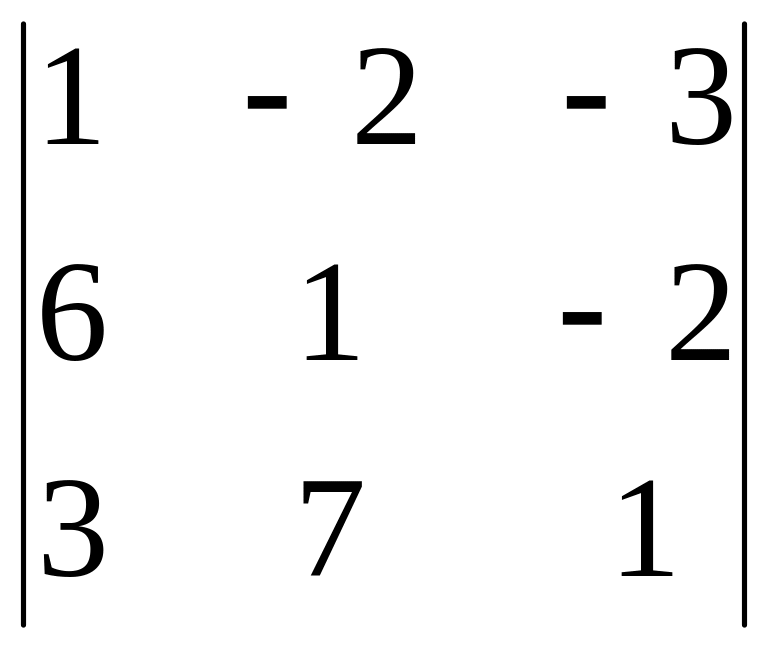 2.2.
2.2.
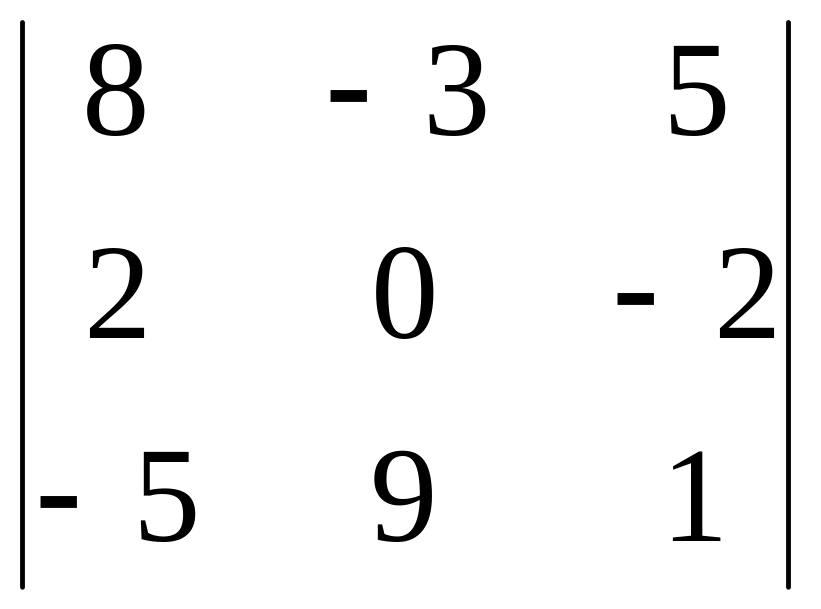 2.3.
2.3.

2.4.
 2.5.
2.5.
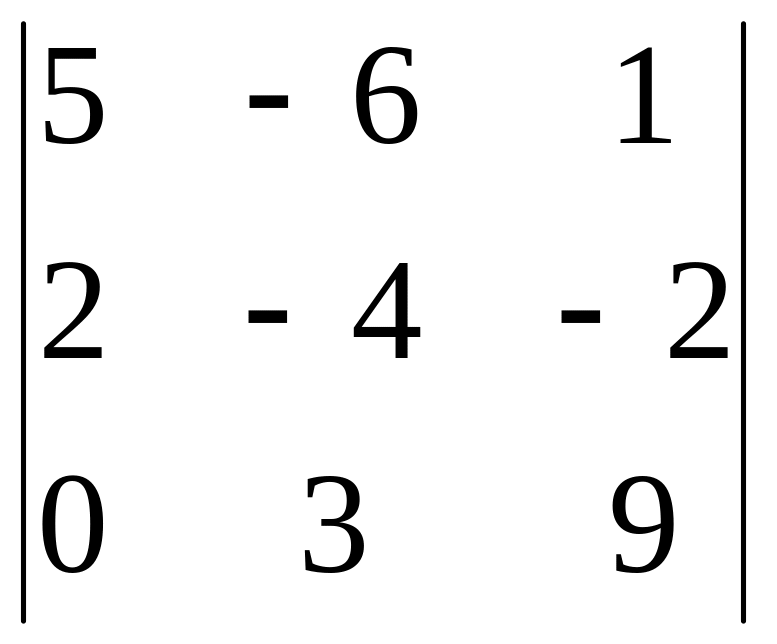 2.6.
2.6.
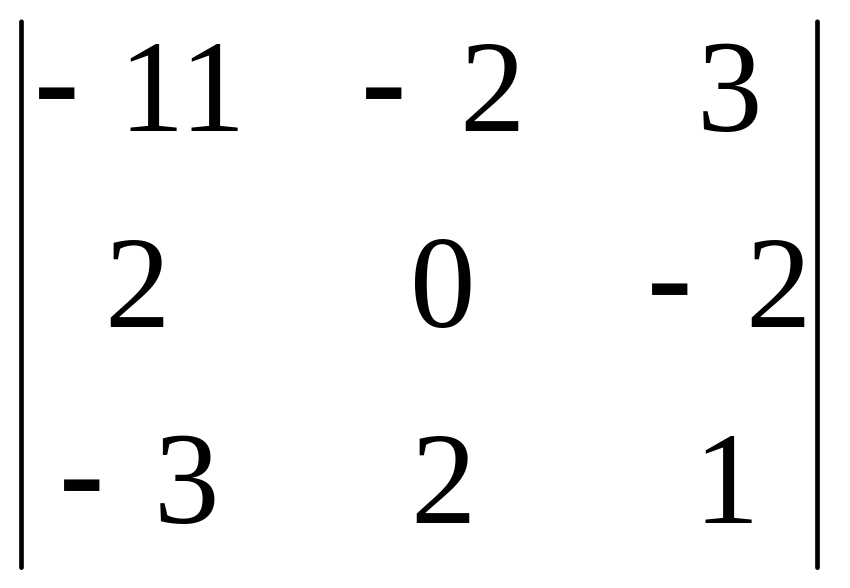
2.7.
 2.8.
2.8.
 2.9.
2.9.
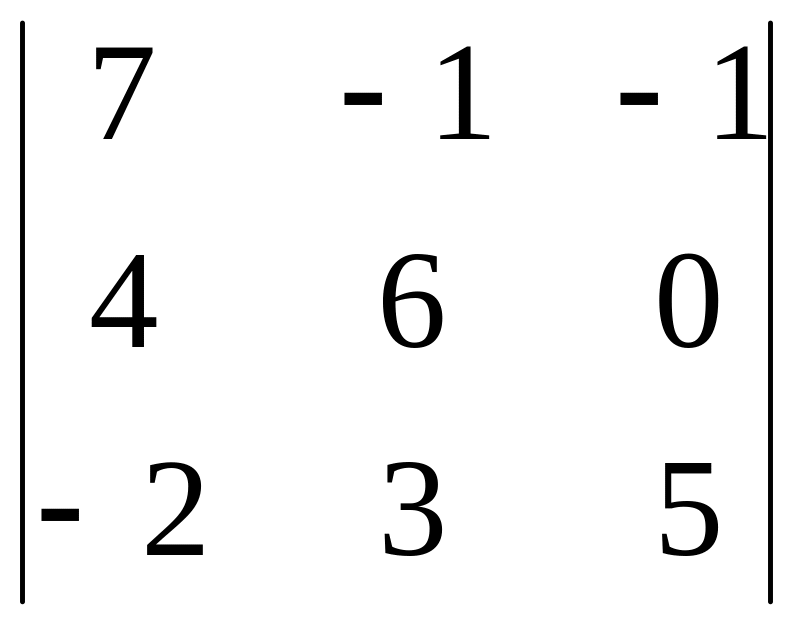
2.10.
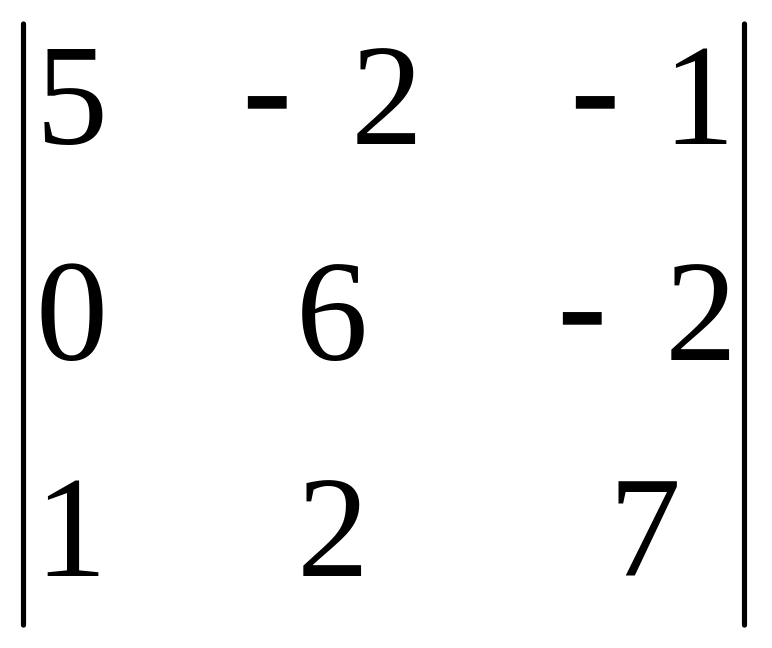 2.11.
2.11.
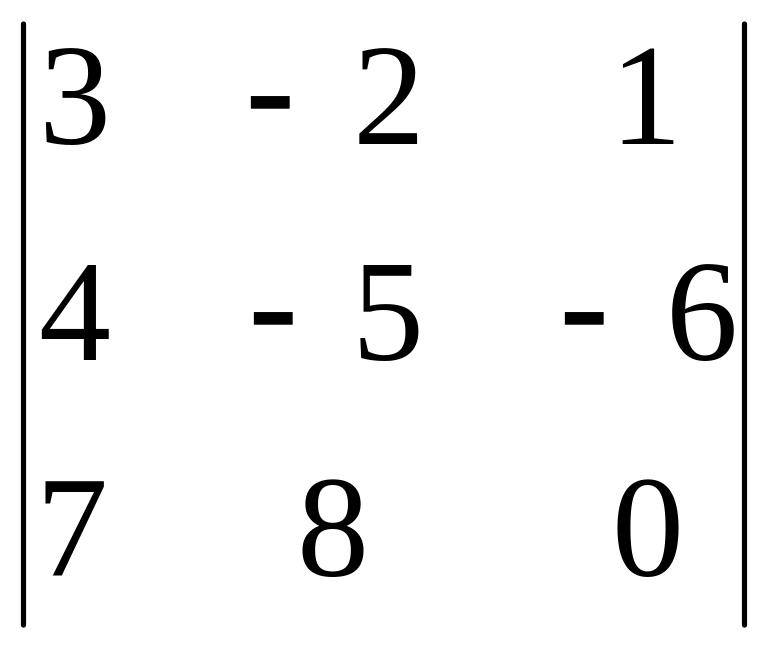 2.12.
2.12.
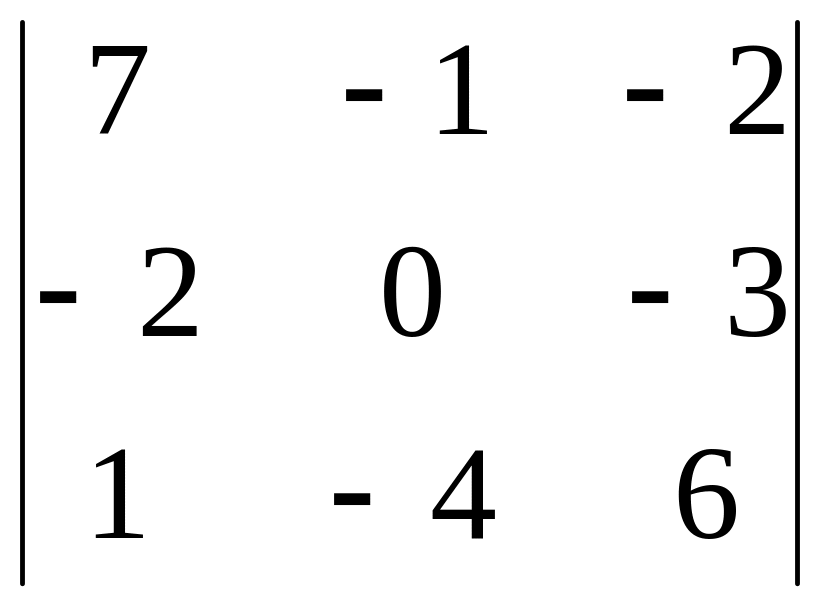
2.13.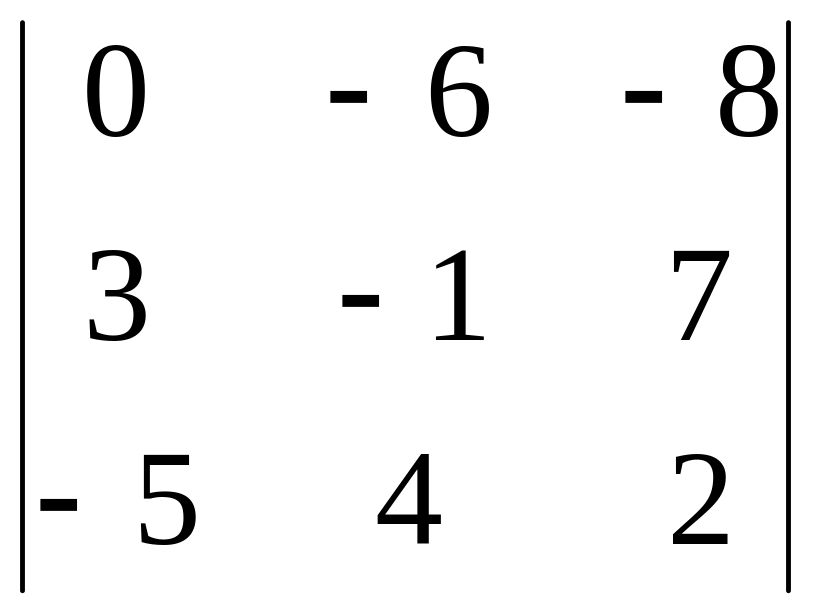 2.14.
2.14.
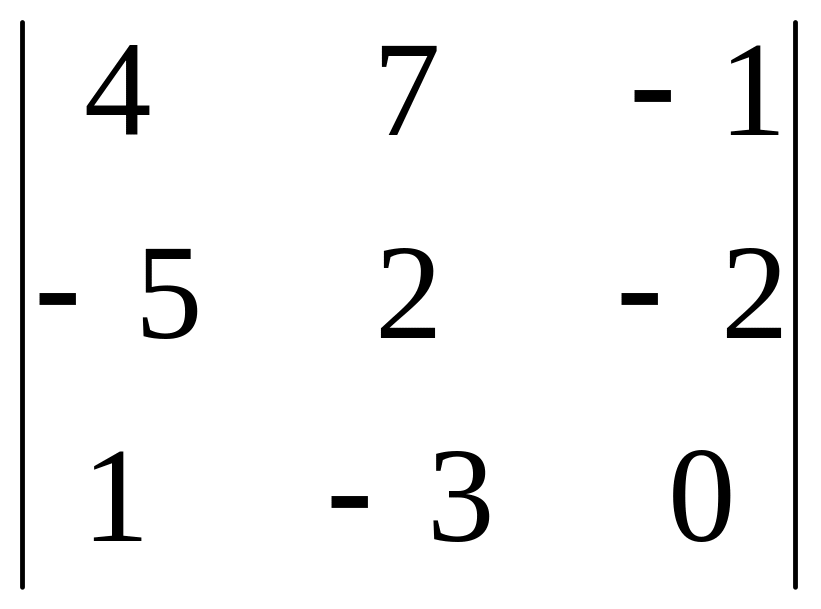 2.15.
2.15.

2.16.
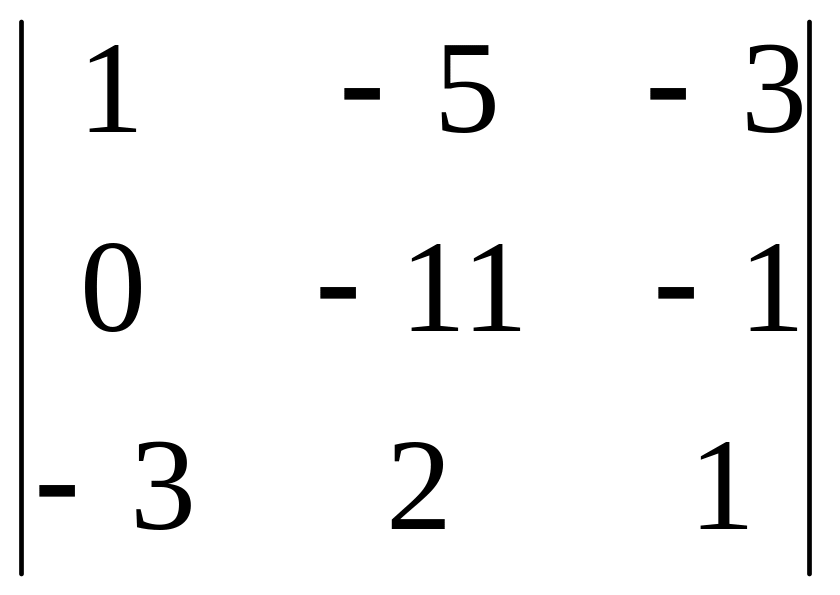 2.17.
2.17.
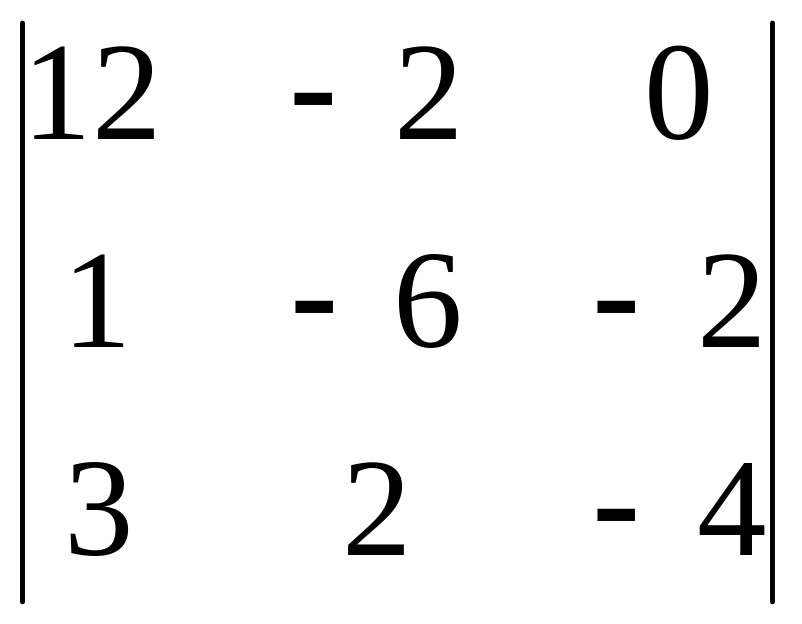 2.18.
2.18.

2.19.
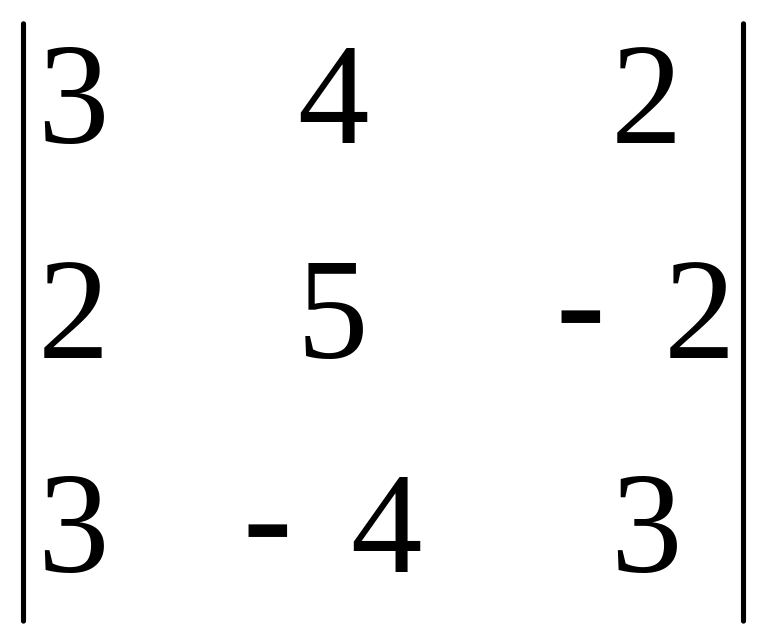 2.20.
2.20.
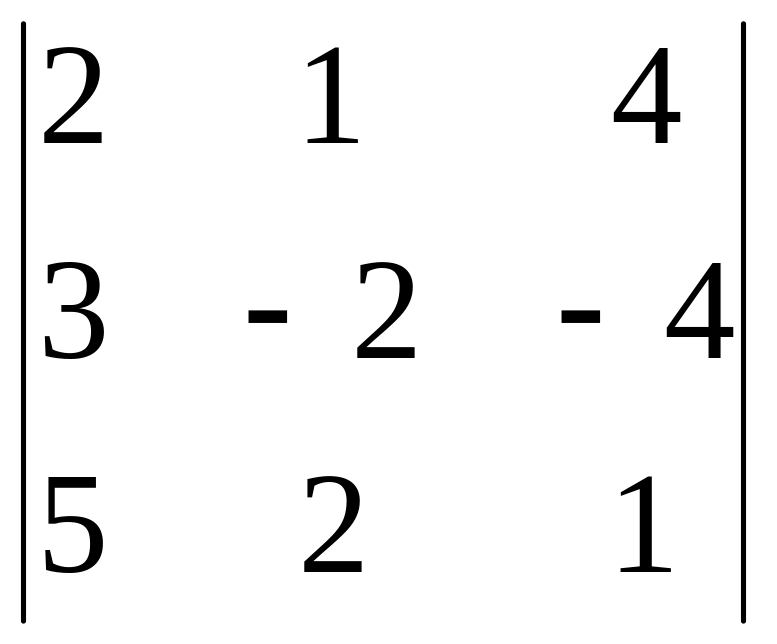 2.21.
2.21.
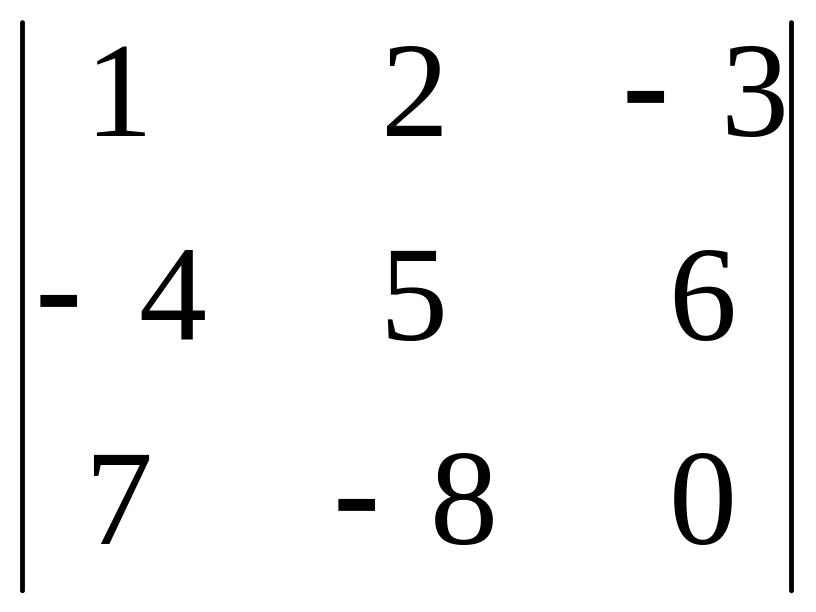
2.22.
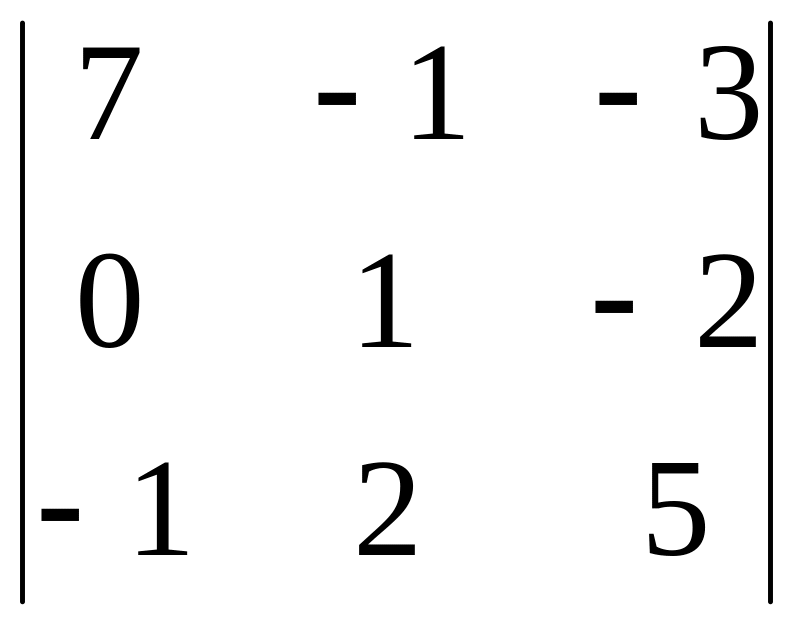 2.23.
2.23.
 2.24.
2.24.
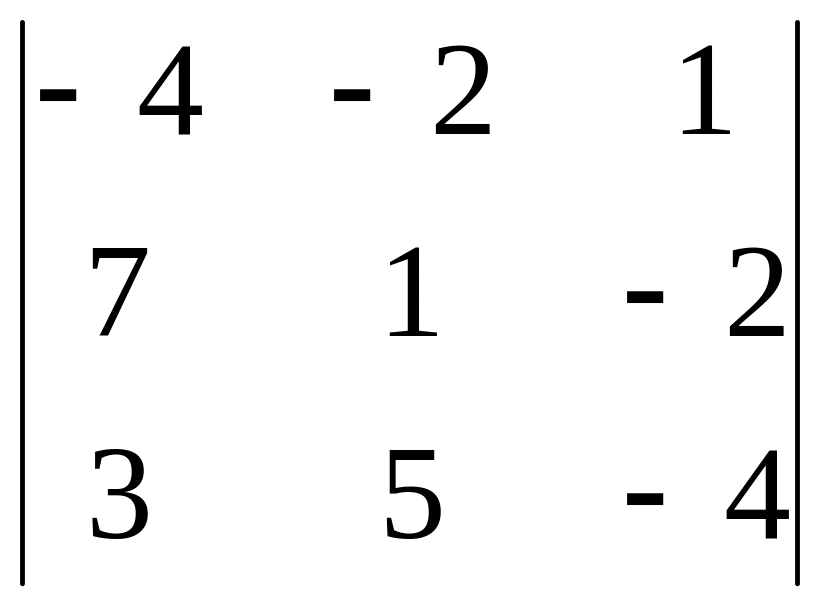
2.25.
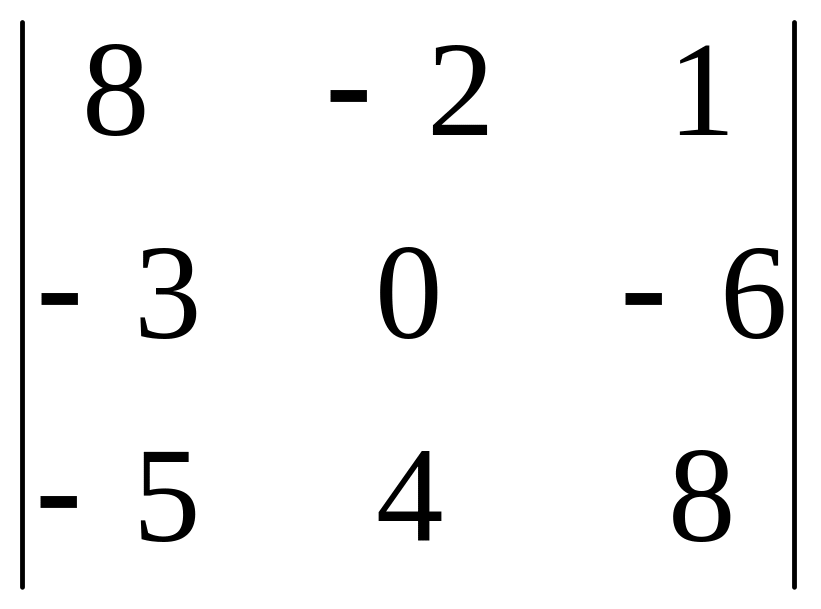 2.26.
2.26.
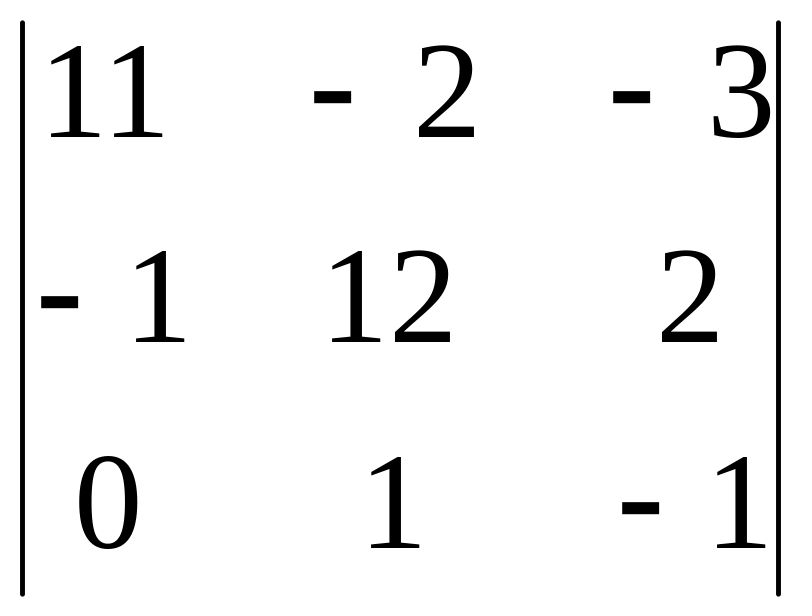 2.27.
2.27.

2.28.
 2.29.
2.29.
 2.30.
2.30.

Задание №3.
Вычислить определитель, обнулив элементы (кроме одного) какой-либо строки или столбца исходной матрицы.
3.1.
 3.2.
3.2.
 3.3.
3.3.

3.4.
 3.5.
3.5.
 3.6.
3.6.

3.7.
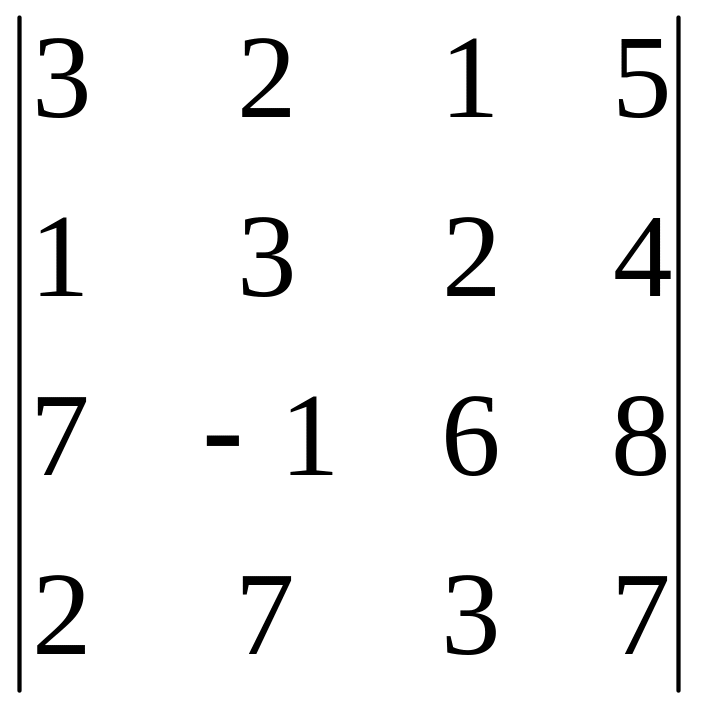 3.8.
3.8.
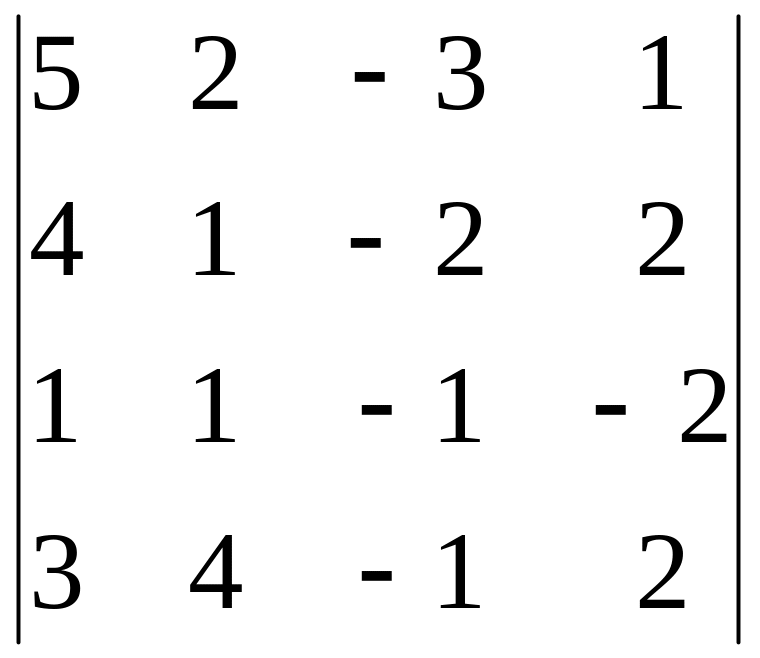 3.9.
3.9.
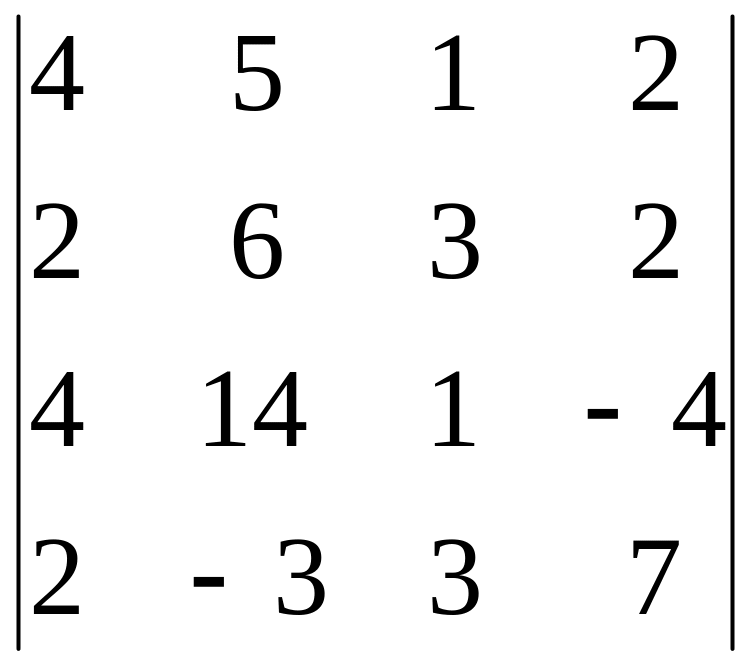
3.10.
 3.11.
3.11.
 3.12.
3.12.

3.13.
 3.14.
3.14. 3.15.
3.15.
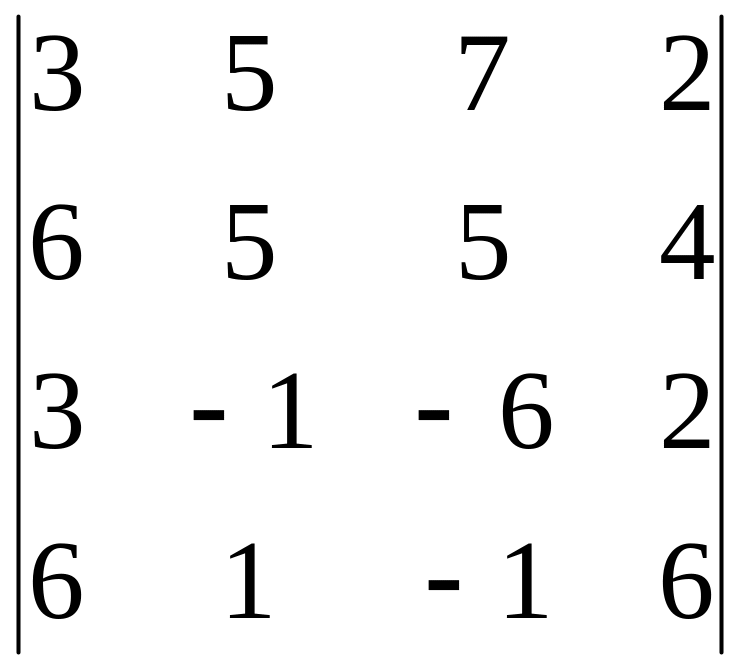
3.16.
 3.17.
3.17.
 3.18.
3.18.

3.19.
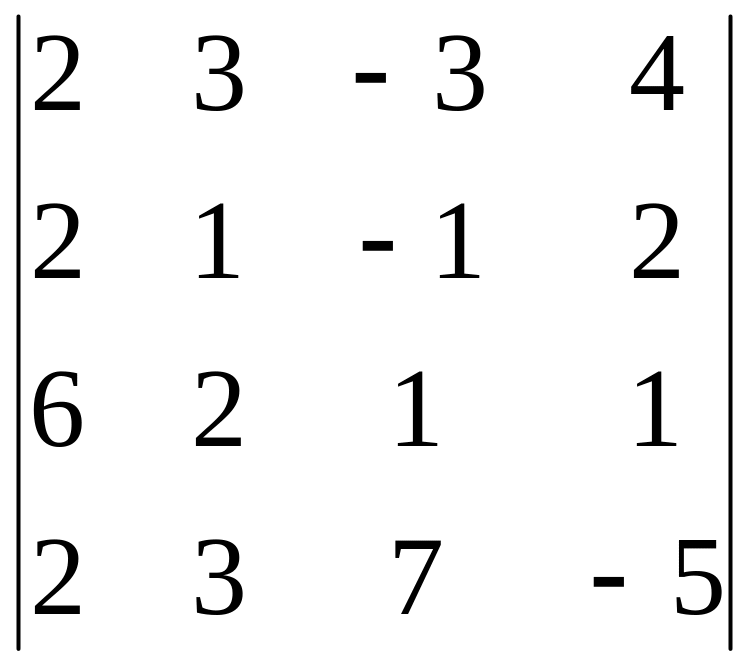 3.20.
3.20.
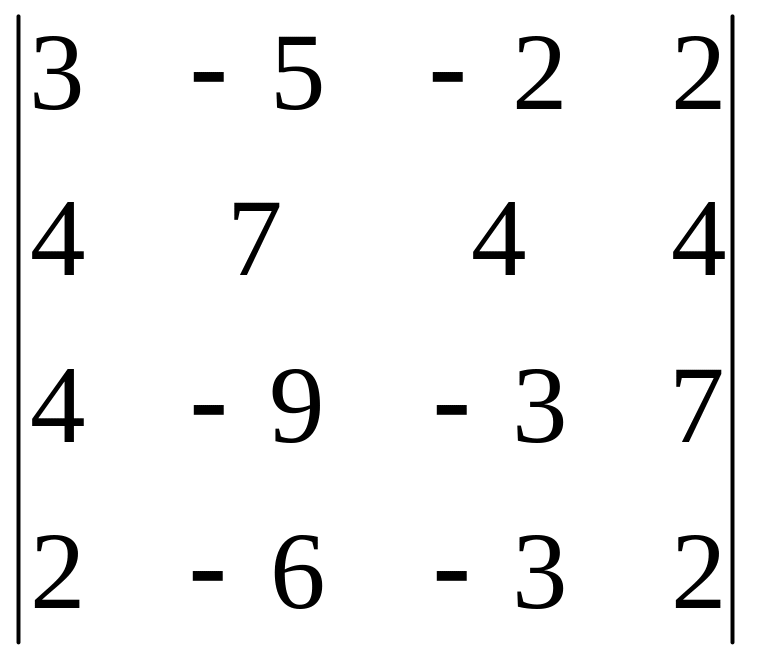 3.21.
3.21.

3.22.
 3.23.
3.23.
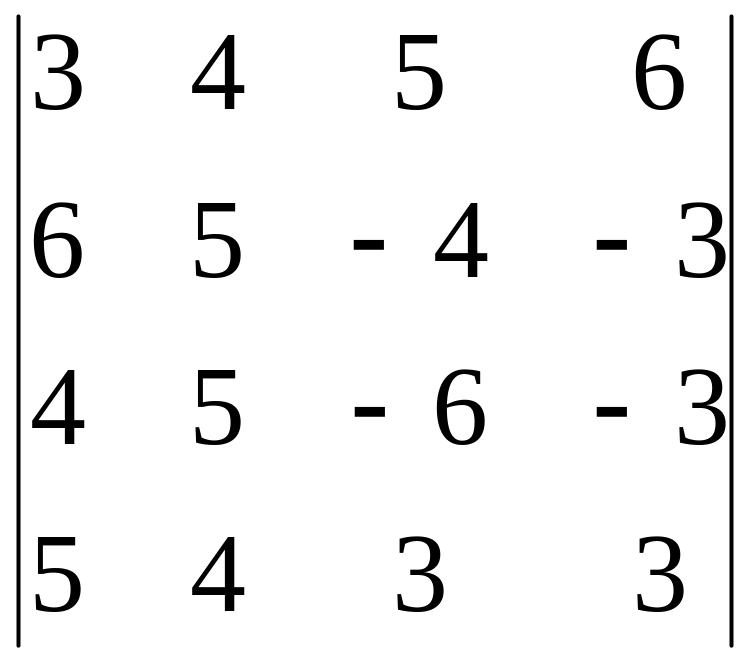 3.24.
3.24.
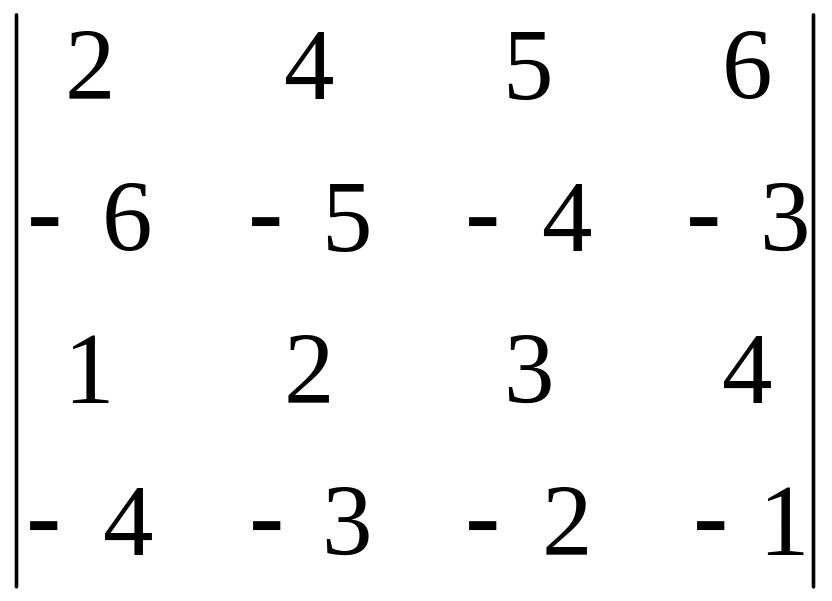
3.25.
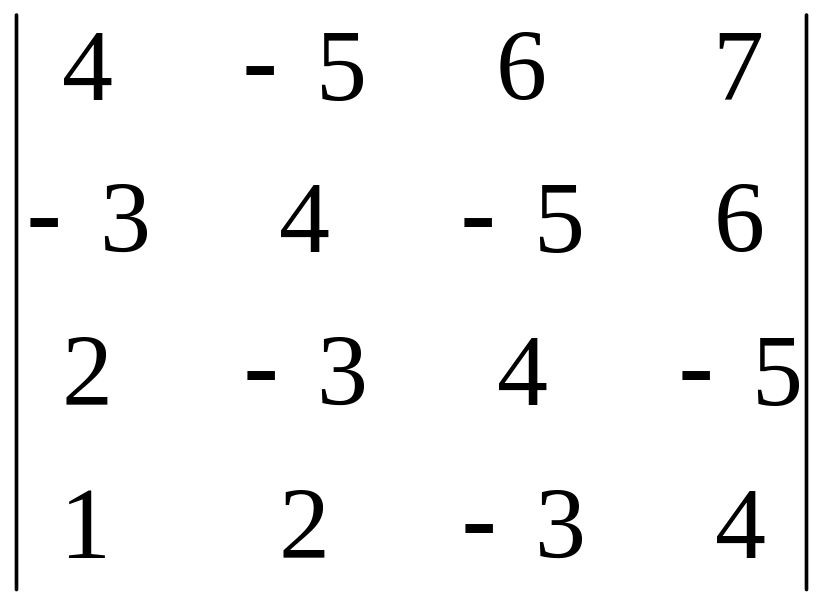 3.26.
3.26.
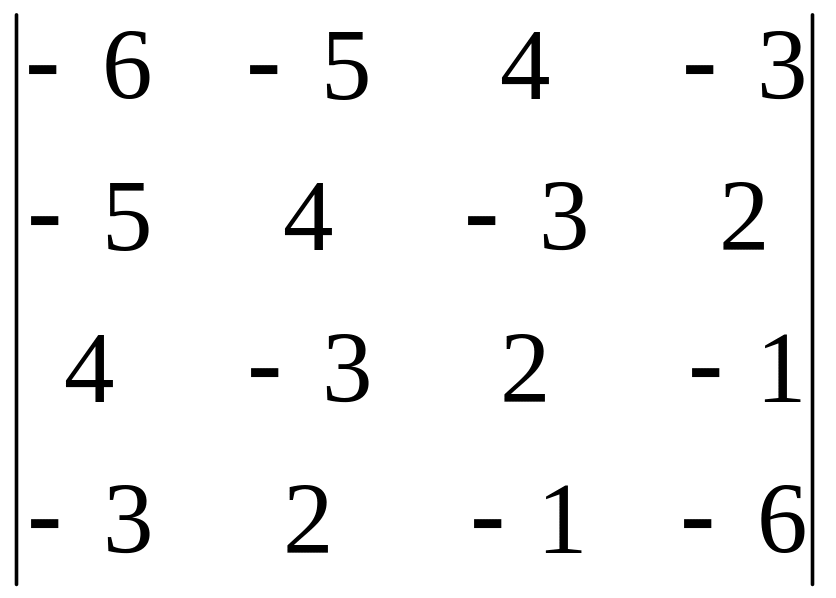 3.27.
3.27.

3.28.
 3.29.
3.29.
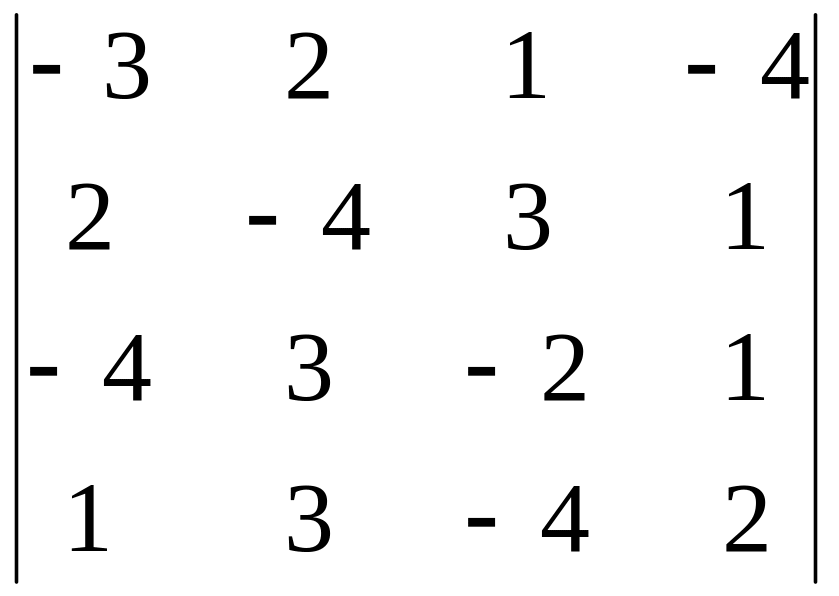 3.30.
3.30.

