Пример выполнения задачи № 10

Таблица 9

№ варианта	Q, H	а, м	в, м	h, см	Схема по рис. 37
1	100	1	1,5	2	а
2	50	2	1	3	б
3	60	1	0,5	1	а
4	70	1	1,5	2	б
5	80	2	0,5	3	а
6	90	1	1	2	б
7	120	1	1,5	3	а
8	110	2	1	1	б
9	100	1	0,5	2	а
10	50	1	1,5	3	б
11	60	2	0,5	2	а
12	70	1	1	3	б
13	80	1	1,5	1	а
14	90	2	1	2	б
15	120	1	0,5	3	а
16	110	1	1,5	2	б
17	90	2	0,5	3	а
18	120	1	1	1	б
19	110	1	3	2	а
20	50	2	1	2	б

Дано: Q = 100Н, Н = 0,02м, ℓ =2,0 м. Рис. 38.

Решение

1. Определим реакции на опорах, считая, что усилие Q приложено статически

; ,

, ,

; , , .

Проверим правильность определения реакций:

, , 50 – 100 + 50 = 0, 0 = 0.

2. Определим опасное сечение в балке (случай статического нагружения, см. рис. 39).

1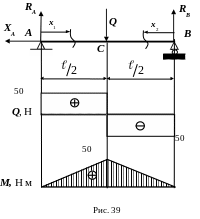 -й участок: 0 ≤ х ≤ ℓ/2, , .

При х = 0; ; М = 0.

При х = ℓ/2; ; .

2-й участок: 0 ≤ х ≤ ℓ/2, , .

При х = 0; ; М = 0.

При x = ℓ/2; , .

Построим эпюры Q и М. Опасное сечение – С (рис. 38).

,

Тогда .

3. Определим коэффициент динамичности из выражения:

.

Определим статическое перемещение точки соударения С, используя метод Максвелла–Мора.

Реакции на опорах грузовой и единичной схемы равны (рис. 40):

, .

.

1-й участок: 0 ≤ х ≤ ℓ/2; , .

2-й участок: 0 ≤ х ≤ℓ/2 ,

Так как ,

Тогда статическое перемещение точки контакта падающего груза (точка С, рис. 40) определяется из уравнения:

.

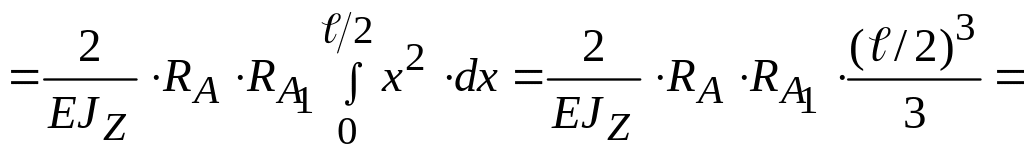
З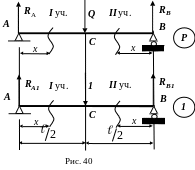 десь учтено, что для двутавра № 10 I_z = 198 см⁴.

Коэффициент динамичности: , то есть величины статических прогибов и напряжений при ударном приложении нагрузки возрастут в 86,9 раза.

Динамический прогиб в точке удара: δ_дин = δ_статичК_д = 0,0053 ×86,9 = 0,46 мм.

П роверим прочность балки в опасном сечении. σ_max ≤ [σ].

86,9×50/(39,7×10^-6) = 109×10⁶ Па = 109 МПа ≤ 160 МПа.

Условие прочности выполняется.

З А Д А Ч А № 11