Расчет динамического давления при переезде неровности системы с конечным числом степени свободы.
Решение уравнения (69) выписывается численно на ЭВМ. Для этого находится один из следующих численных методов:
1. Метод Рунге-Кутта. (относится к числу прямых методов интегрирования);
2. Метод Ньюмарка.
1) Метод Рунге-Кутта основан на приведении системы (69) к системе уравнений I порядка.
+F=
При численном решении этого уравнения должны быть заданы начальные условия.
1)
При t=0,
;
2)
При t=0,
=0;
3)
При t=0,
;
4)
При t=0,
=0;
Метод Рунге-Кутта позволяет выполнить интегрирование системы уравнений с достаточной точностью, если шаг интегрирования существенно меньше периода высшего тона колебаний.
В противном случае решение задачи будет расходиться.
Для оценки динамичного эффекта при переезде неровности, используется динамический коэффициент, определяемый по формуле:
(71)
После схода с неровности колебания автомобиля и его давления на проезжую часть определяются интегрированием системы (69), в которой в формуле (70) получается h=0.
2) Наряду с прямым методом Рунке-Кутта может использоваться абсолютно устойчивый метод Ньюмарка.
Сущность его заключается в переходе от дифференциальных уравнений (69) к алгебраической системе уравнений. Благодаря введенным гипотезам от изменений ускорения на данном шаге.
Решение уравнения осуществляется наиболее эффективными методами на каждом шаге интегрирования. Выбор шага интегрирования зависит от характера решения и точности его представления. При этом решение является абсолютно, но не учитываются высшие гармоники.
Определение критических скоростей движения автомобиля через неровность.
Для двух массовой модели критическим является 2 скорости движения.
определяется совпадением с низшей чертой автомобиля
(72)
2)
определяется совпадения
с
(73)
Динамические модели современных автомобилей.
1) Трехосный автомобиль с балансированной тележкой.
Для кузова (подрессоренной части автомобиля) используется 2 степени свободы
1) - вертикальное перемещение
2)
-
угловой поворот в продольной плоскости
Для балансирования тележки 2 степени свободы:
1)
угол поворота
2)
вертикальные перемещения
2) Сдельный автопоезд
О – момент инерции во вращательном движении относительно седла
Лекция №9
Вынужденные колебания систем с конечным числом степ. Свободы при силовом гармоническом возмущении.
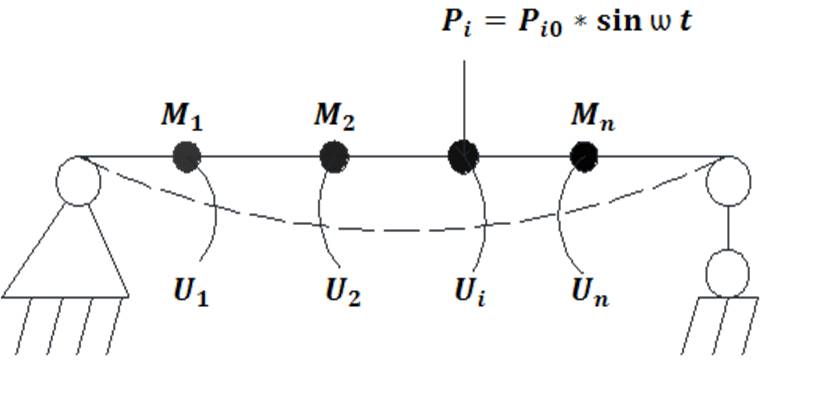
Предположим только одну возможную силу, заданную по 3-му.
Для расчёта динамической системы на движение нескольких сил достаточно получить решение для одной из действующих сил. Последние примеры независимости действия сил позволяет применить решение для нескольких сил.
В первом приближении. Рассмотрим движение при отсутствии сил сопротивления.
M +CU=P
+
+
+…
=0
+
+
+…
=0
……………………………………………….. (a)
+
+
+…
=
………………………………………………..
+
+
+…
=0
Имеем систему д.у. 2-го порядка с постоянными коэффициентами.
В общем случае решение будет складываться из свободных колебаний с собственными частотами и вынужденных колебаний с частотой возмущения.
Т.к. свободные колебания через некоторое время затухают, то возн. установ-ся пр-сс вынужденных колебаний с частотой возмущающей силы, => в установившемся режиме задачей исследования является определение амплитуд колебаний системы по формулам:
=
=
…………………. (б)
=
(в)
…………………………….
После двукратного дифференцирования, приведения подобных членов, и сокращения:
……………………………………………………………………………………. (г)
……………………………………………………………………………………
Получили неоднородную систему алгебраических уравнений относительно амплитуд перемещений.
Для решения воспользуемся методом определителей, по формулам Крамера.
;
;….;
;
(д)
(е) ∆= ……………………………
(ж)
=
……………………………
…………………………..
По теореме Безу определитель
(е) можно представить в виде:
∆=
*
…..
(з)
Где
-
собственные частоты заданной системы.
=
*
…..
(и)
-
парциальные
собственные частоты рассматриваемой
системы, если на i-тый
инертный элемент наложить связь,
препятствующую перемещению.
Подставляя (з) и (и) в (д), получим.
=
(74)
Проанализируем выражение (74)
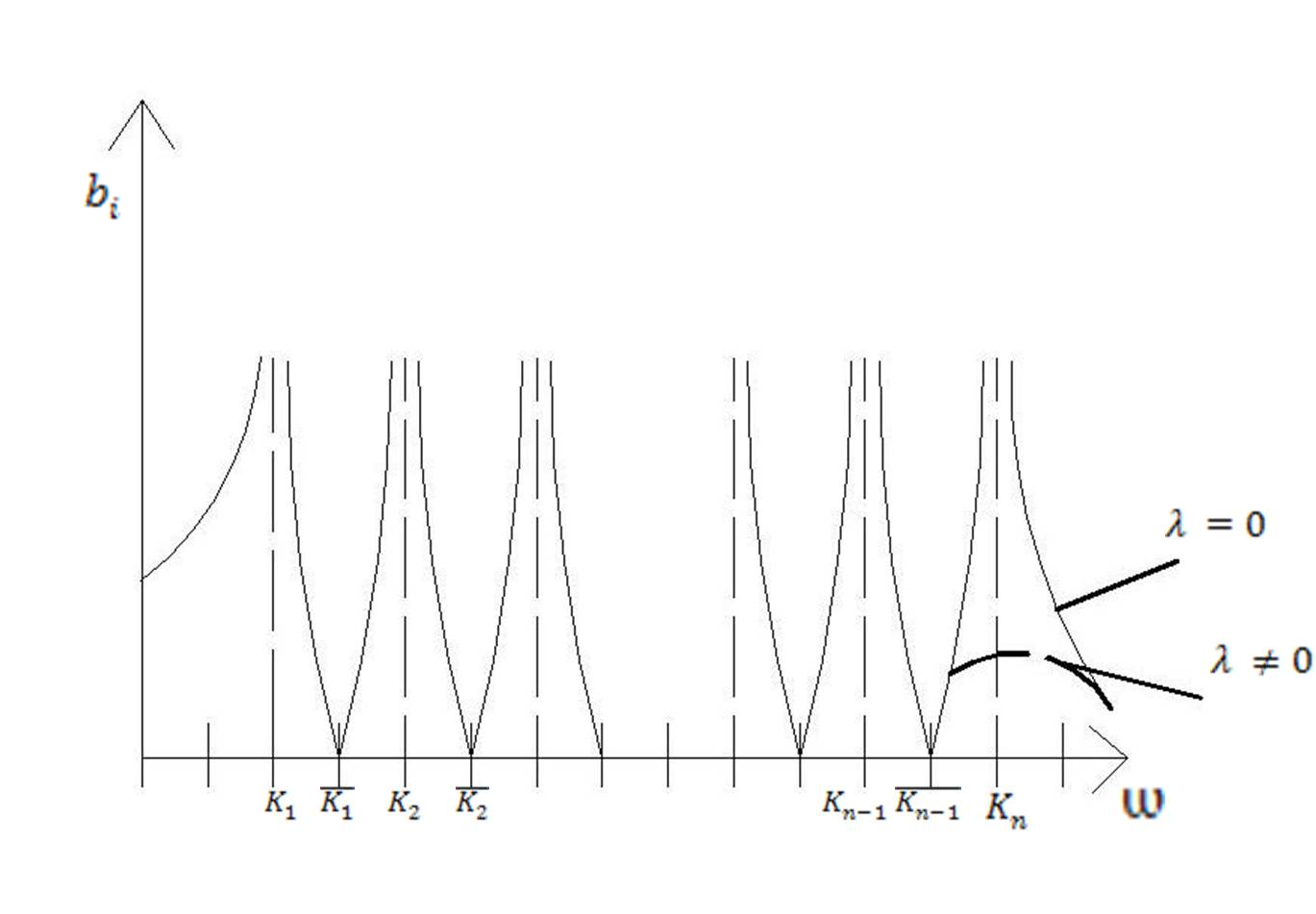
Зависимость амплитуды от частоты колебаний.
При приближении частоты возмущения к собств. ч-те заданной системы амплитуда колебаний возрастает.
При
отсутствии сопряжения возрастает до
При
приближении ѡ - частоты возмущения к
парц. ч-те
амплитуда колебаний обращается в нуль.
При учете трения резонансные явления не приводят к бесконечному возрастанию амплитуд колебаний.
Наиболее сильно резонанс развивается на низших собств. частотах системы.
При учете сил сопряжения, эффект уменьшения амплитуд колебаний до нуля снижается.
Это явление положено в основу мероприятий по колебаний, которое называется Виброгашением.