Динамические модели автомобилей в виде систем с конечным числом степеней свободы.

Динамические модели автотранспортных средств могут быть плоскими и пространственными.

I. Плоская модель 2^X осного автомобиля

M - масса

Q - момент инерции

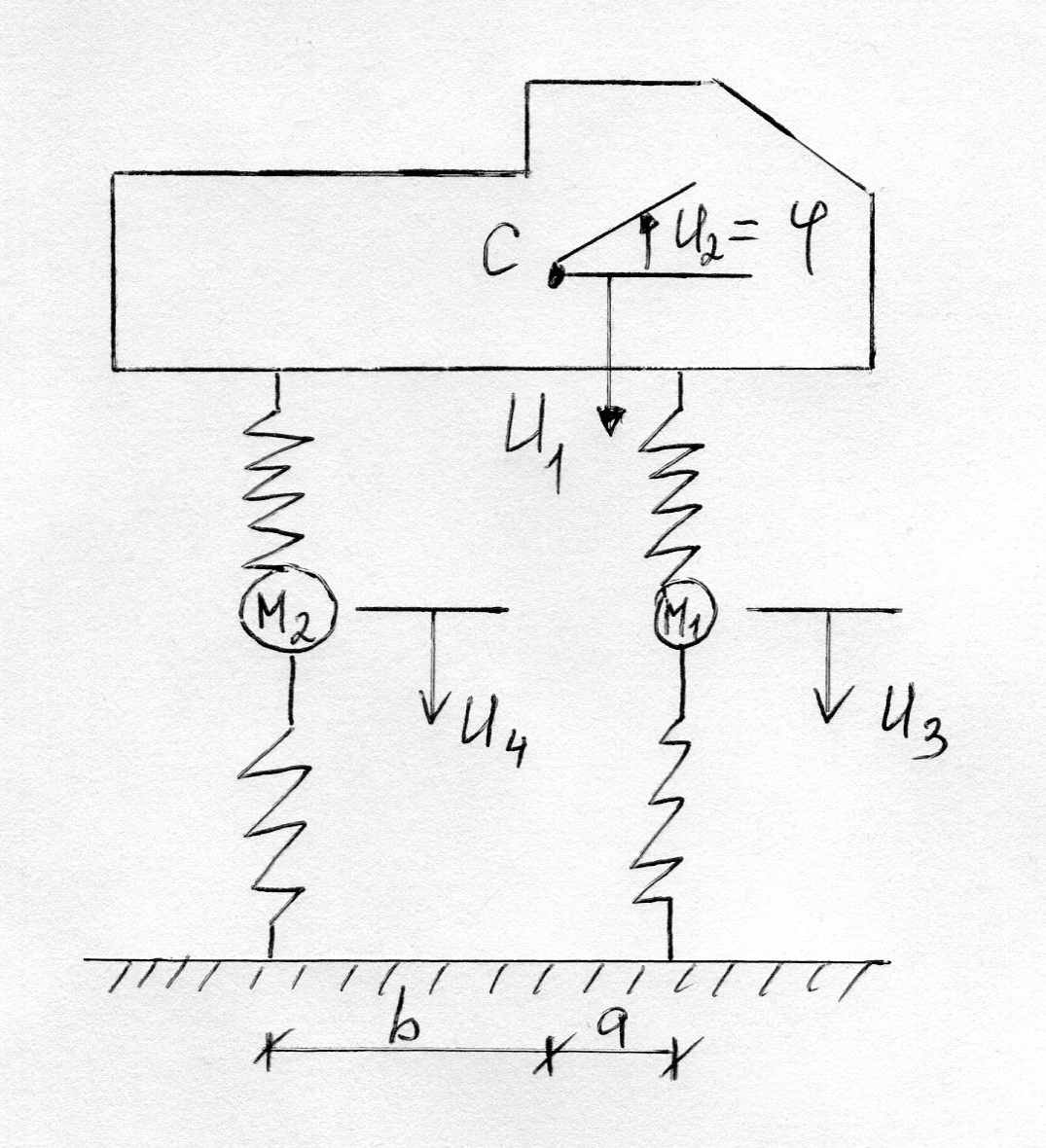
U₁ - вертикальное перемещение кузова

U₂ = φ - угол поворота кузова в продольной плоскости

U₃ - вертикальное перемещение передней оси

U₄ - вертикальное перемещение задней оси

При движении с постоянной скоростью по дороге можно такую модель описать системой с 4мя степенями свободы.

Плоские модели 2х-осной модели при условии, когда

θ≈Mab , могут быть представлены в виде 2х независимых расчетных схем.

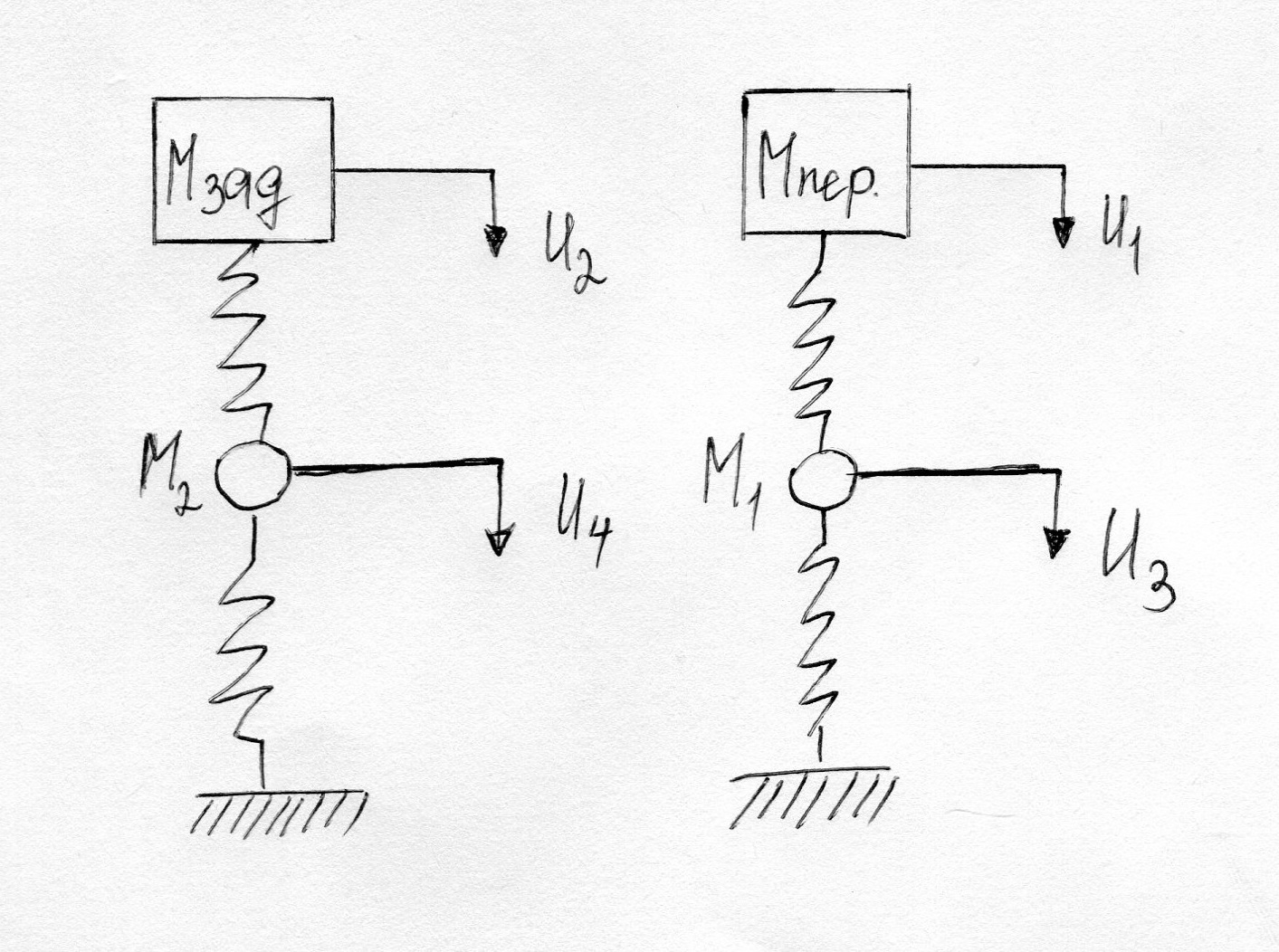
В автомобилях шины и рессоры моделируются нелинейно упругими связями.

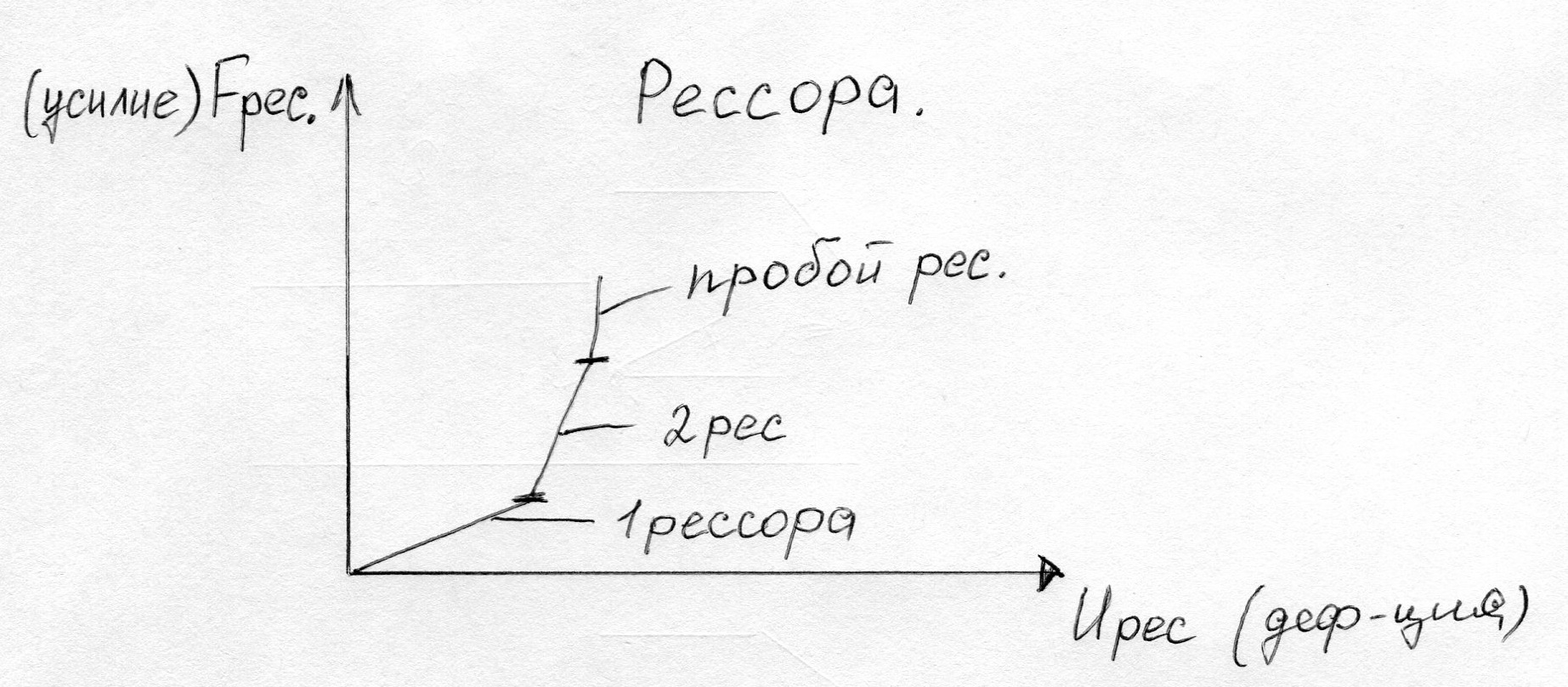
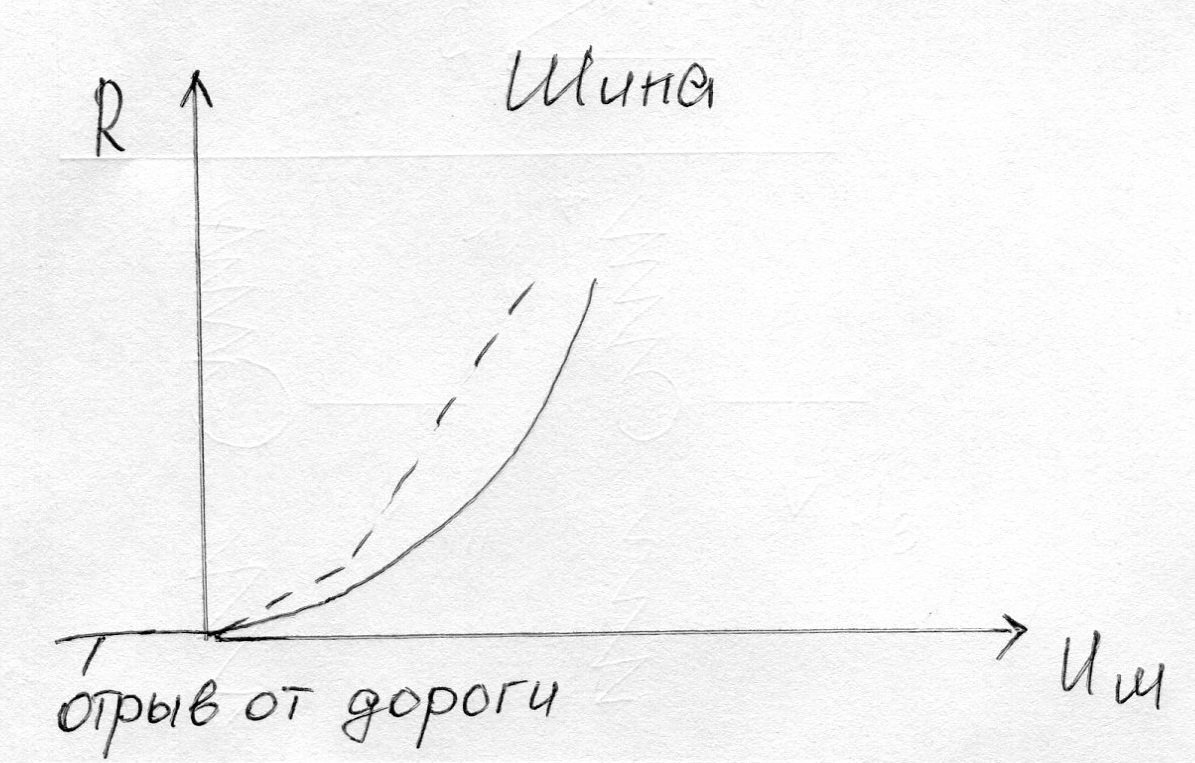
II. Пространственная модель автомобиля.

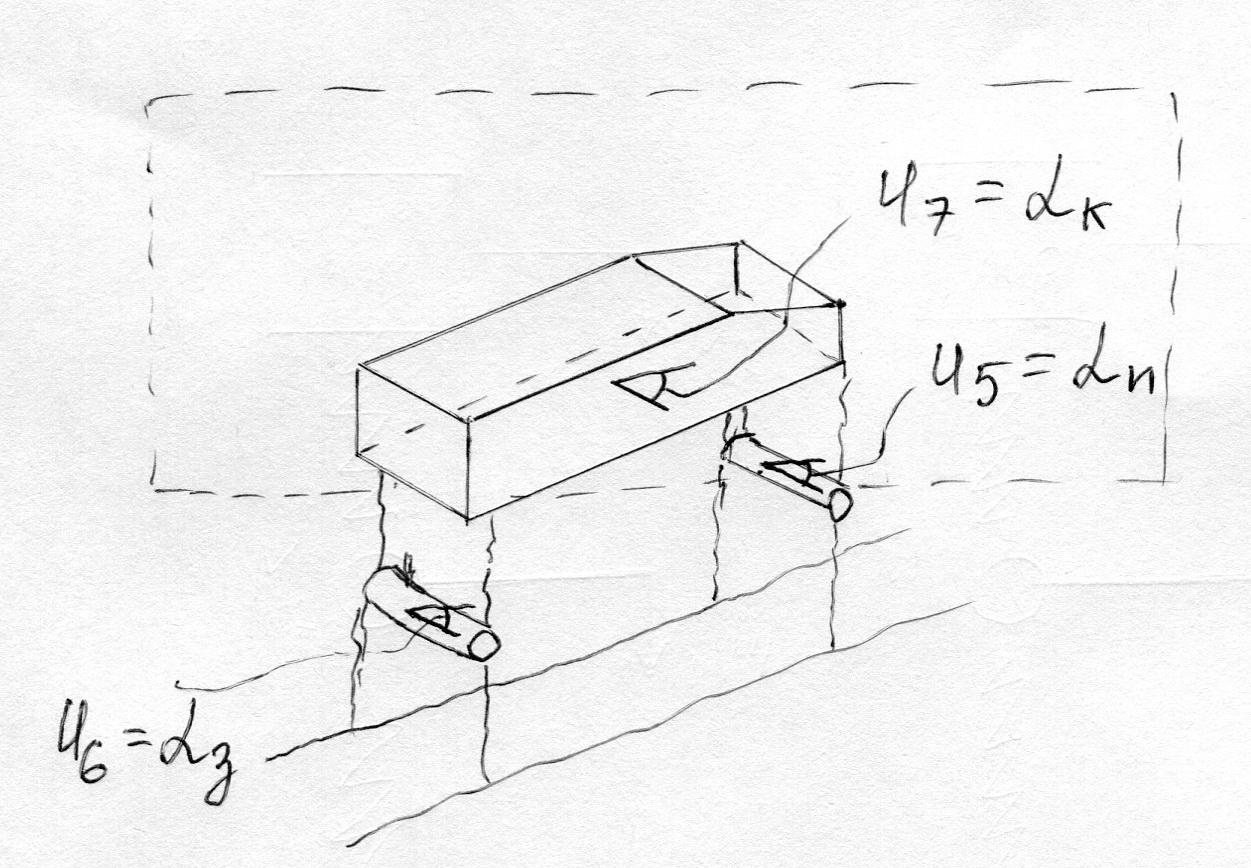
U5=α_n - поперечный крен передней оси;

U6=α_з - поперечный крен задней оси;

U7=α_к - поперечный крен кузова.

Дополнительно к 4м степеням свободы плоской модели.

Плоская модель может использоваться при одинаковых микропрофилях под левой и правой колеёй.

Матрица жесткости 2х массовой модели автомобиля.

Система с 2мя степенями свободы.

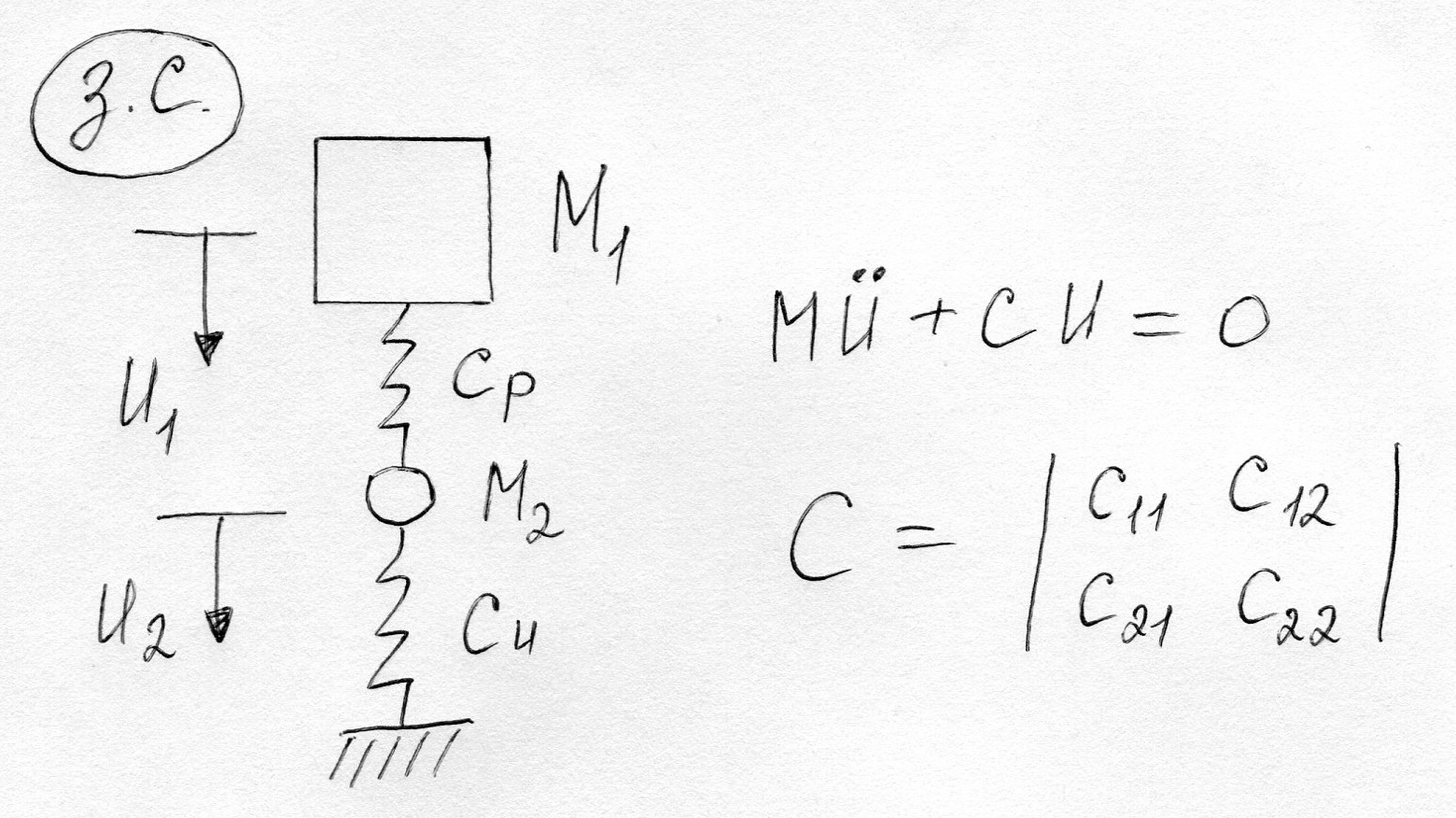
Примем основную систему метода перемещений

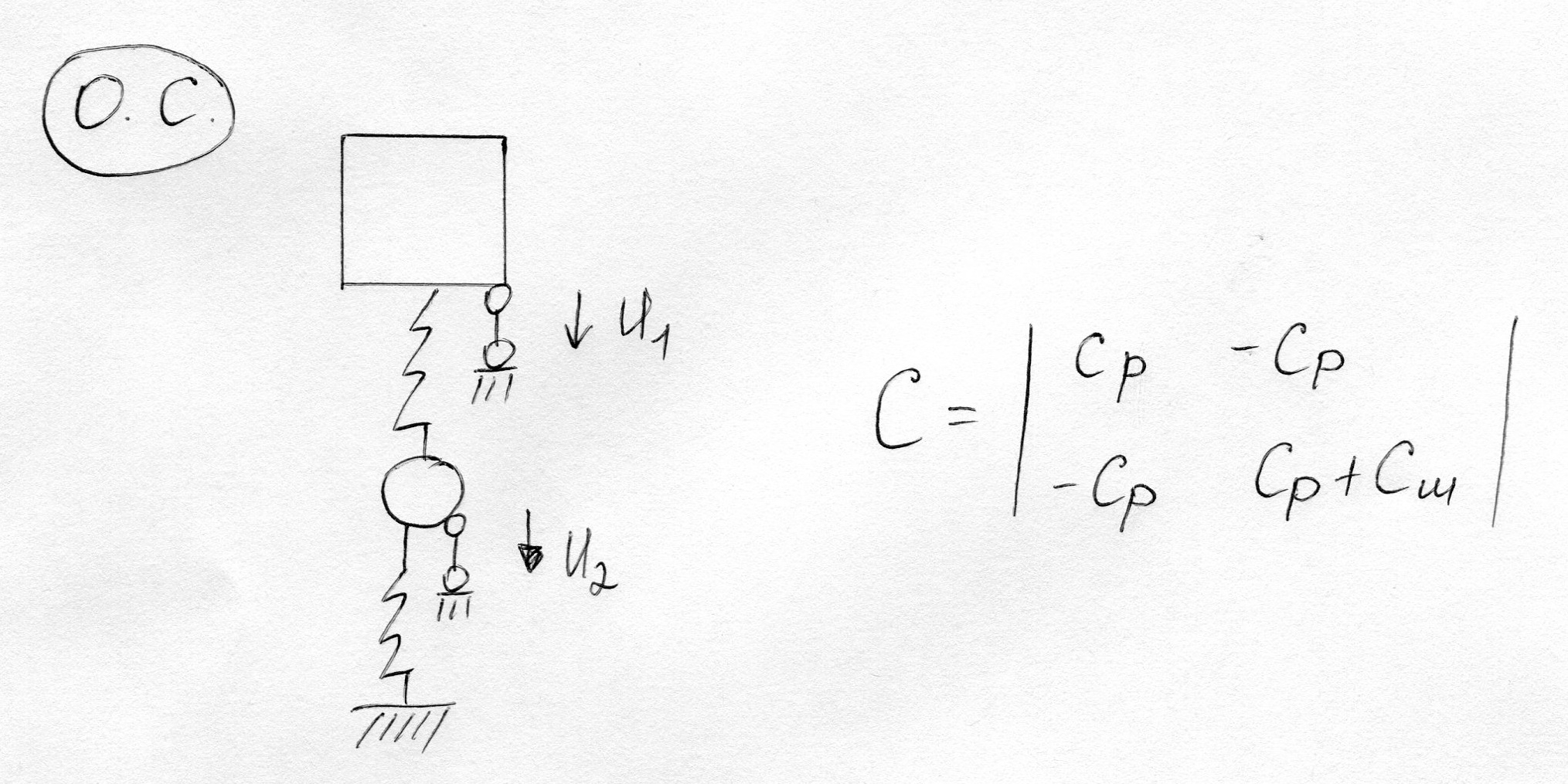
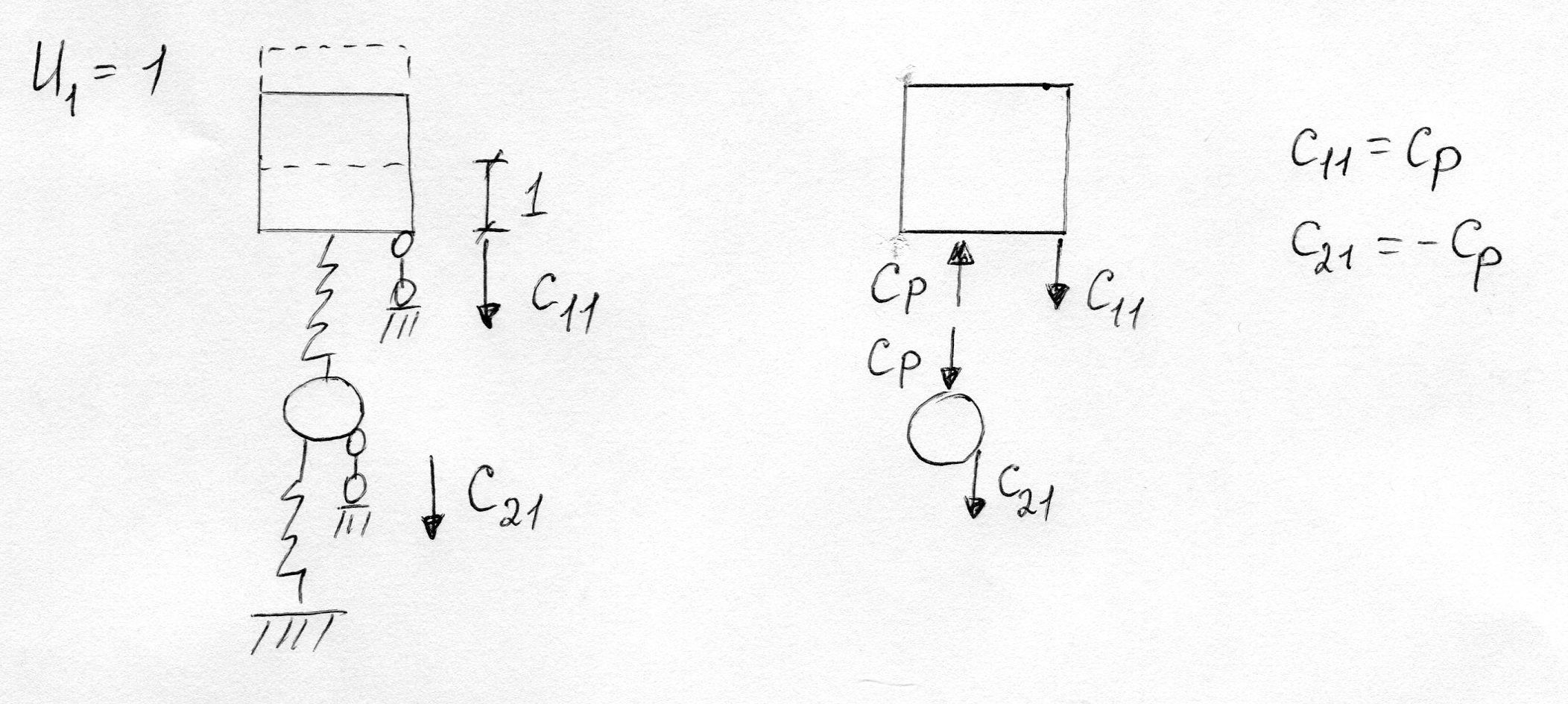
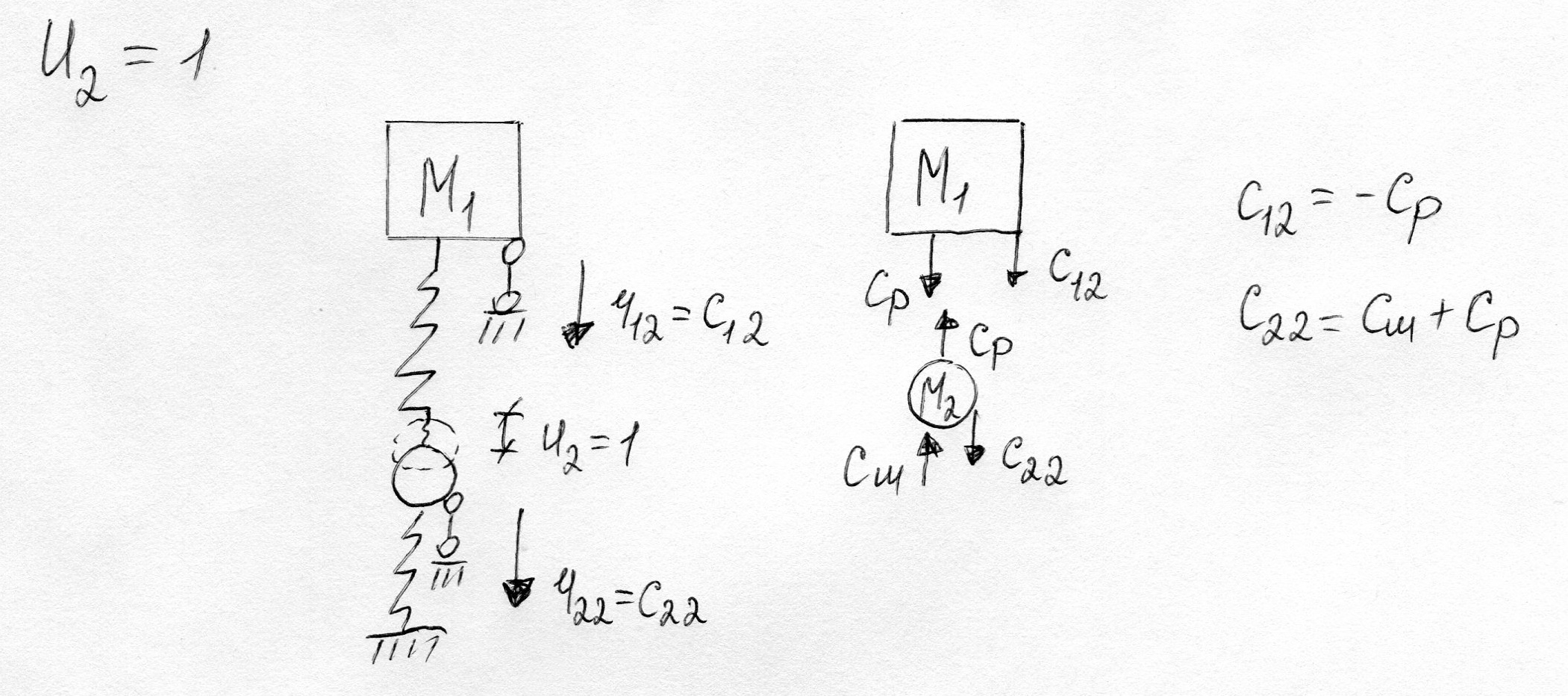
Отметим, что в матрице жесткости так же, как и в матрице коэффициентов канонических уравнений метода перемещений, выполняются два условия:

1. Главные коэффициенты положительны

2. Побочные коэффициенты, симметричные относительно главной диагонали, равны между собой.

с_ij=c_ji

Вычислим собственные частоты 2х массовой модели.

Подставим в формулу (г) (перед (65))

= 0

(С₁₁-М₁∙k²)(С₂₂-М₂∙k²)-C₁₂∙C₂₁=0

M₁∙M₂∙k⁴-(M₂∙C₁₁+M₁∙C₂₂) ∙k² - C₁₂²+C₁₁∙C₂₂ = 0

(k²)² - ( ) ∙k² - ∙ (C₁₂²-C₁₁∙C₂₂) = 0

k²_1,2= ∙ ( ) = 0

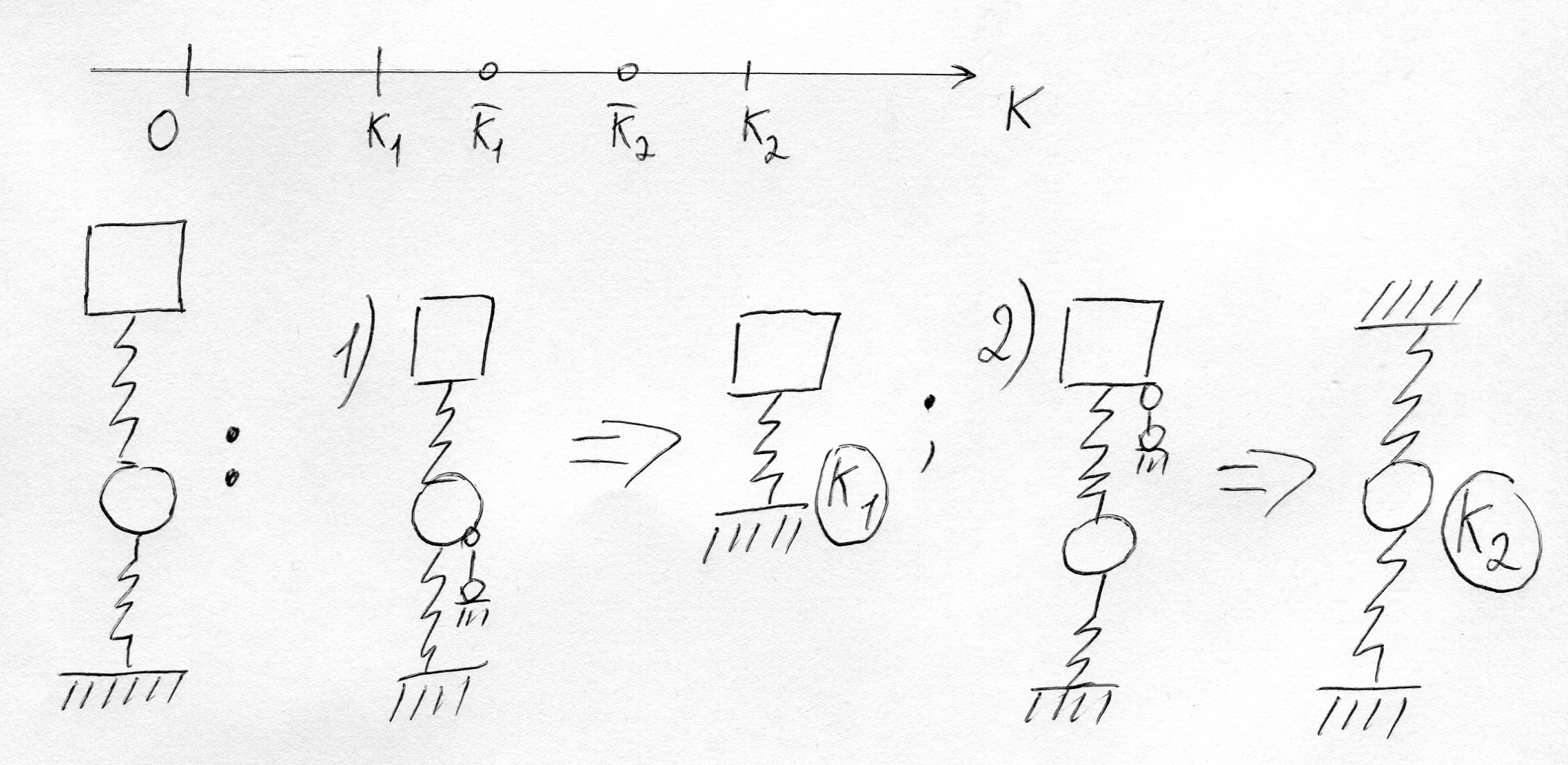
Парциальные системы для 2х массовой модели совпадают с приближенными значениями частот 1 массовой модели, и их частоты находятся между частотами 2х массовой модели.

Переезд 2х массовой модели через неровность.

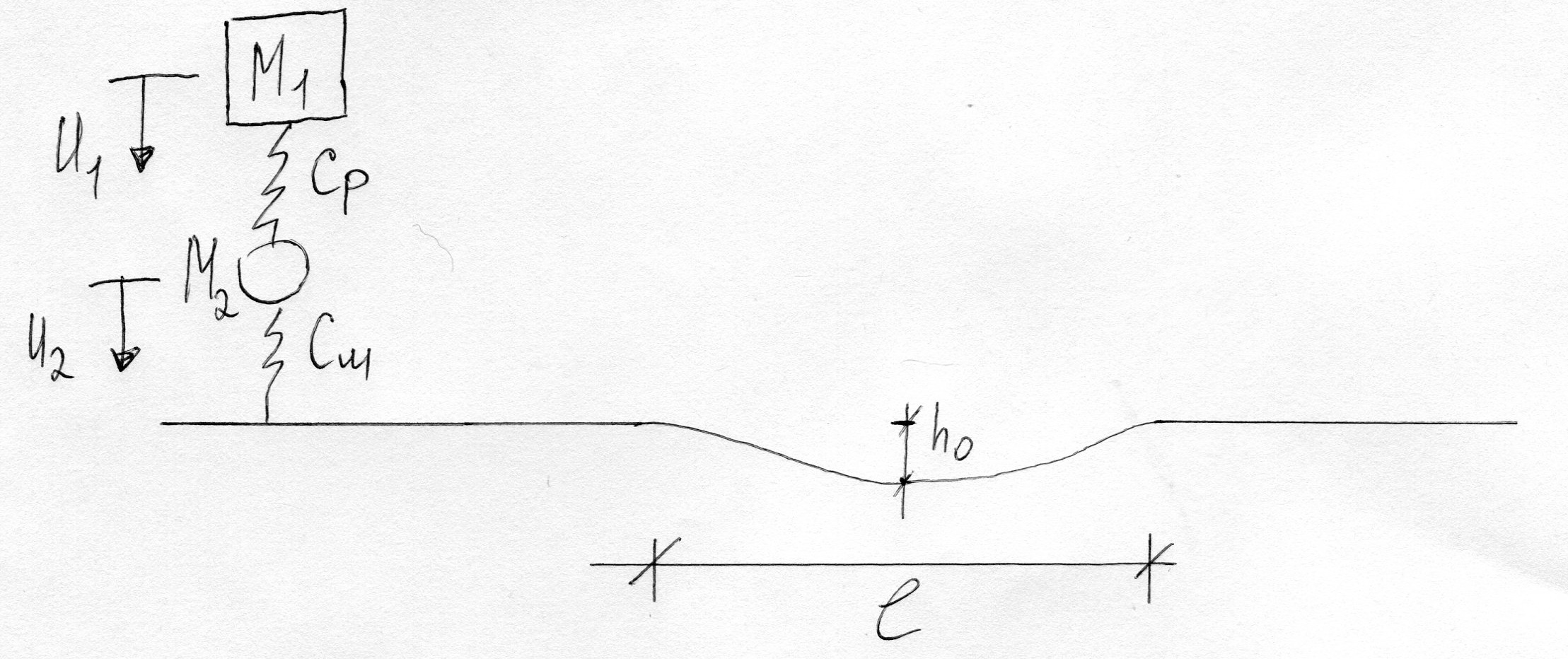
h(t)= (1-cos ) = (1-cos ),

где ω =

M +CU=P(t) (а)

Дифференциальное уравнение без учета сопротивления можно записать в следующем виде, который можно получить из уравнения (а):

(69)

F(ν)- усилие в рессоре, является функцией дифференциации в рессоре.

F(ν) = f(ν), ν=U₂-U₁ - в линейном случае.

F(ν) = С_p(U₂-U₁)

R(w) - давление автомобиля на проезжую часть

R(w)=f(w), w = U₁ - h (1)

R(w)=C_ш(U₁-h)

(70)

В уравнении (69) в отличии от формул учтены силы собственного веса.

Лекция № 8

Переезд двух массовой модели через неровность.

;

где

(а)

Дифференциальные уравнения без учета сопротивления можно записать в следующем виде, которое можно получить из уравнения (а)

(69)

F(v) - усилие в рессоре, является функцией дифференцирования в рессоре.

F(v)=f(v), - в линейном случае.

F(v)=

R(w) - давления автомобиля на проезжую часть.

R(w)=f(w), w= -h(l)

R(w)=

(70)

В уравнении (69) в отличие от функции учтены силы собственного веса.