1) Внешние:
Fвн. = F (t) – направим в направлении положительного перемещения системы.
2) Силы инерции:
–
направим в противоположную
сторону Fвн
(или перемещения).
3) Силы неупругого сопротивления (трения).
–
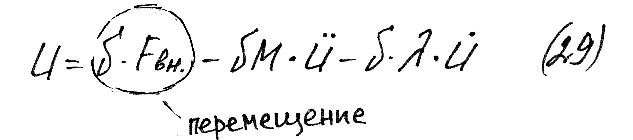вынужденные колебания
системы с сопротивлением.
–
свободные колебания
системы с сопротивлением (частный
случай).
–
свободные колебания
системы без сопротивления.
(5)
Свободные затухающие колебания системы с одной степенью свободы при наличии вязкого трения.
Будем использовать для описания колебаний дифференциальное уравнение в прямой форме.
(18)
Обозначим
(а), разделим на массу.
-
дифференциальное уравнение II порядка
с постоянным коэффициентом.
(21)
Рассмотрим два возможных варианта решения:
1.Случай большого сопротивления ( > k)
2. Случай малого сопротивления ( < k).
корни будут комплексны
-
частота системы с трением
Пусть
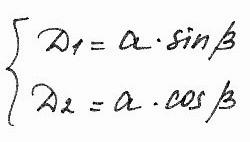перейдем к одночленной форме записи,
заменяя D1 и D2
на a и b.
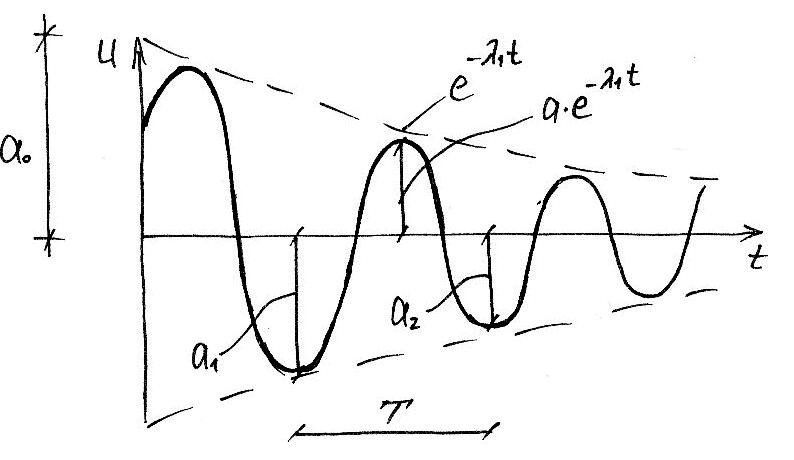
Колебание такой системы представляет собой затухающую синусоиду, у которой амплитуда уменьшается со временем, а частота колебаний отличается от частоты колебаний системы с трением.
Оценим влияние трения на частоту и амплитуду.
Для конструкций, у которых развивающееся максимальное трение 1 оценивается в ней
1 = 0,1 k (*)
Подставим (*) в (36)
Влияние трения на частоту свободных колебаний оценивается величиной не больше 0,2 %, поэтому в расчетах собственных частот в строительных конструкциях влиянием трения можно пренебречь.
Оценим влияние трения на амплитуду колебаний.
Для описания степени затухания введем величину, равную ln отношению соседних амплитуд.
1 = 0,1 k;
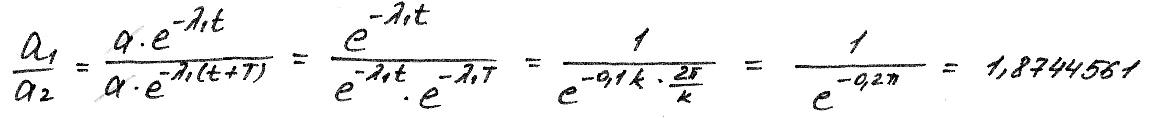
При сильном колебании амплитуда уменьшается почти в 2 раза за 1 период.
Для различных материалов логарифмический декремент () составляет:
- для бетона 0,3 – 0,4
- для стали 0,1 – 0,15
- для дерева 0,15 – 0,2
Амплитуда и начальная фаза в случае затухающих колебаний определяется из начальных условий.
1) при t=0, U=U0
2) при t=0, U’=U0’
Подставим первое условие в (34)
D1= U0
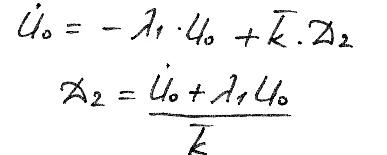
Сопоставляя (38) и (39) с формулами (27) и (28), замечаем, что сопротивление оказывает влияние и на амплитуду, и на начальную фазу.
Вынужденные колебания системы с одной степенью свободы при наличии силового гармонического возмущения.
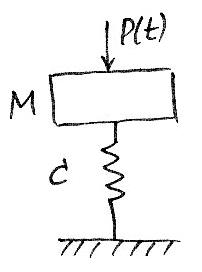Рассмотрим колебания на основе уравнения
в прямой форме, при этом в первом
приближении не будем учитывать затухающие
колебания. В качестве возмущения будем
использовать гармоническую функцию.
Р0 – амплитудное значение возмущающей силы.
Такое силовое возмущение является широко распространенным, например, воздействие на строительную конструкцию при работе станка с эксцентрично расположенной вращающейся частью.
(17) (без λ*U')
Это дифференциальное уравнение II порядка неоднородное, его решение можно записывать в следующем виде: Uон = Uоо + Uчн
Uоо – решение уравнения MÜ + сU = 0
Найдем Uчн:
– собственная частота.
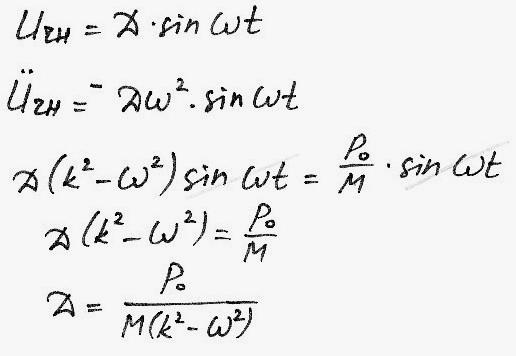
Лекция № 3