Понятие коэффициента жесткости для систем с 1 степенью свободы.

Наряду с коэффициентом податливости в динамических расчетах используется коэффициент жесткости (с).

с – величина силы (пары сил) которую необходимо приложить к инертному элементу, чтобы вызвать его единичное перемещение (линейное или угловое)

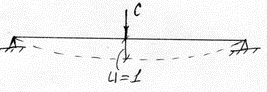
(5)

Определение и при последовательном и параллельном соединении упругих связей.

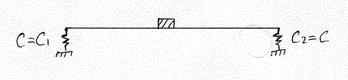
Воспользуемся вычислением , путем суммирования перемещений за счет деформирования каждой связи.

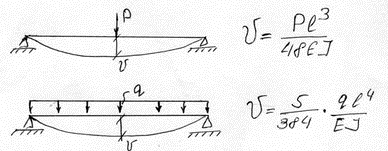
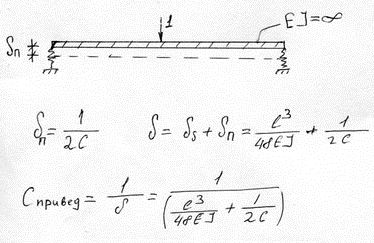
Решение этой задачи основывается на принципе независимости сил, в соответствии с которыми перемещения от действия совокупности сил равно сумме перемещений от каждой силы в отдельности.

Упругие связи при своем соединении могут быть соединены по одной из следующих схем:

1. Параллельное соединение

2. Последовательное соединение

1. Параллельное соединение

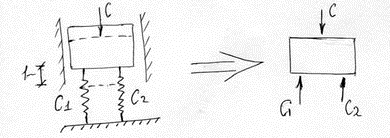
С-С₁-С₂=0; С= С₁+С₂ (6)

При параллельном соединении упругих связей, коэффициенты жесткости складываются.

2, Последовательное соединение

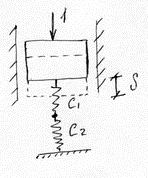
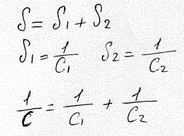
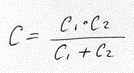(7)

Лекция № 2

Дифференциальное уравнение движения систем с одной степенью свободы.

В зависимости от применения характеристик упругих связей, используются две формы уравнения движения:

1. Прямая форма – на основе использования коэффициента жесткости c.

2. Обратная форма - на основе коэффициента податливости .

1)Прямая форма:

Вывод уравнения движения будем выполнять на основе правила Даламбера.

В соответствии с этим правилом к действующим на конструкцию силам присоединяются силы инерции, которые в случае поступательного движения равны , а в случае вращения ;

Рассмотрим все силы, действующие на тело:

1) Cобственный вес инертного элемента ;

2) Силы упругости

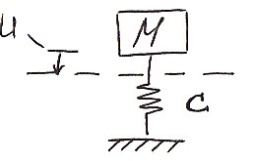
Формула (11) применима только для линейно-деформируемых систем tg =c.

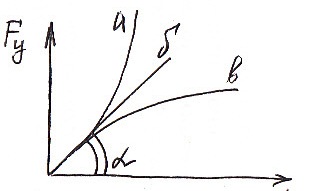
а) жесткая характеристика жесткости;

б) линейная характеристика жесткости;

в) мягкая характеристика жесткости.

(кусочно-линейная)

В нелинейных деформируемых системах характеристика жесткости является переменной.

3) Силы неупругого сопротивления (силы трения).

Они могут быть представлены по одной из моделей:

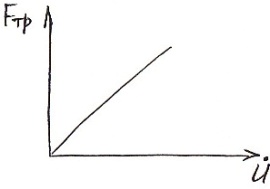
- сила вязкого сопротивления (сила трения зависит от скорости перемещения).

λ – коэффициент вязкого сопротивления.

-модель сухого трения (сила Кулона).

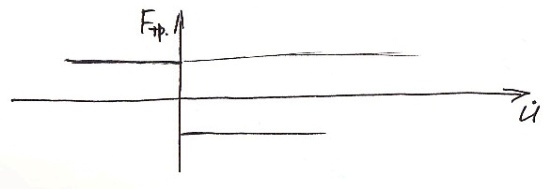
-модель Сорокина. Она является комплексной, в ней силы терния представлены вещественной и мнимой частями.

- действительная часть, которая описывает величину силы трения.

i- мнимая часть, и описывает величину запаздывания трения по сравнению с другими нагрузками.

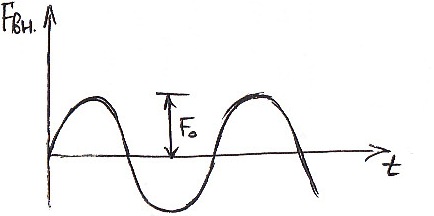
4) Силы возмущения.

Внешние силы могут описываться в зависимости от характера нагрузок различными выражениями.

– гармонический характер изменения.

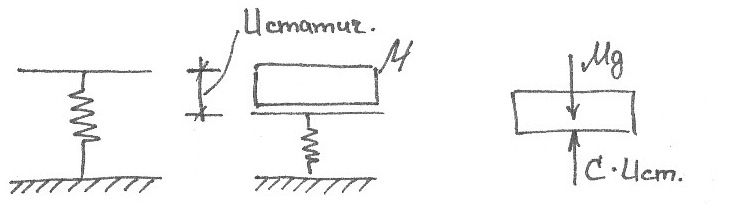
ЗАМЕЧАНИЕ о необходимости учета сил тяжести:

Силы тяжести уравновешиваются силами упругости, возникающими при статическом деформировании связи, поэтому в дальнейшем силы тяжести учитывать не будем. При этом будем отсчитывать отклонение системы от его положения, которое занимает система под действием сил тяжести.

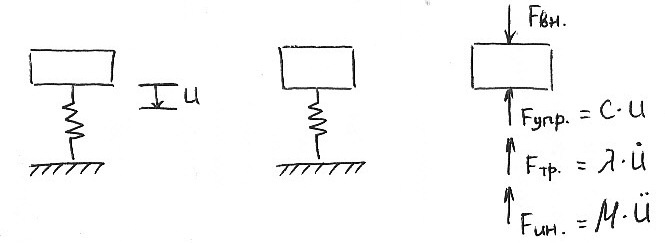
В соответствии с правилом Даламбера для любого положения имеет место механическое воздействие:

- дифференциальное уравнение вынужденных колебаний системы с учетом сопротивления.

- дифференциальное уравнение свободных колебаний с учетом сопротивления.

- дифференциальное уравнение колебаний без учета сил трения.

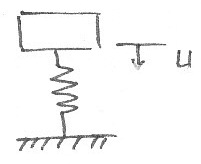
Свободные колебания системы с одной степенью свободы.

Будем исходить из уравнения (19)

(1/м);

- дифференциальное уравнение II порядка с постоянными коэффициентами.

, где

Пусть

(б)  в (а), получим:

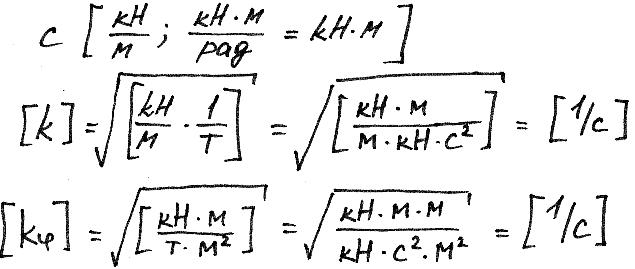
- частота колебаний [1/c]

Бывает двух типов:

- циклическая;

- техническая.

Циклическая частота – количество колебаний за 2 сек.

Техническая частота – количество колебаний за 1 сек.

, [Гц]

Период колебаний – продолжительность одного полного колебания.

,[c]

-начальная фаза (из (20))

а – амплитуда- максимальное отклонение от положения статического равновесия.

Значения а и  определяются по начальным условиям.

Т.к. здесь два параметра, то и условий два:

1) при t=0, U=U0 – начальное перемещение;

2) при t=0, (U’=U0’) - начальная скорость.

Подставим первое условие в (20):

1)

Подставим второе условие в (20 а):

2)

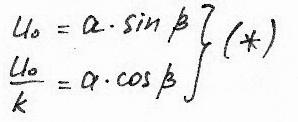
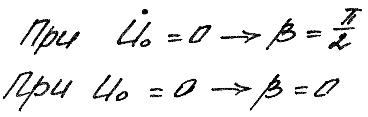
Возведем в квадрат оба (*) и сложим их:

Видим, что амплитуда зависит от начальной скорости и начального перемещения.

При отсутствии сопротивления в системе, колебания носят незатухающий гармонический характер с частотой, которая является собственной для системы.

Изменение собственной частоты возможно, но за счет:

1.изменения инертности (массу, либо момент инерции);

2.изменение жесткости упругой связи.

Дифференциальное уравнение систем с одной степенью свободы в обратной форме.

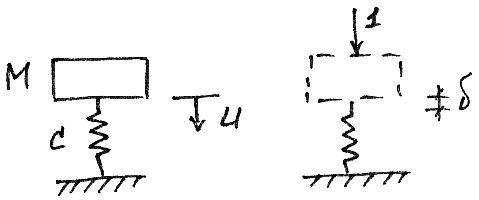
Вывод уравнений движения выполнен на основе правила Даламбера и независимости действия сил.

Кроме фактических действующих сил необходимо учесть силы инерции на ускорение.

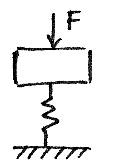F – равнодействующая всех сил, действующих на систему ( в том числе и силы упругости).

Учтем следующие силы: