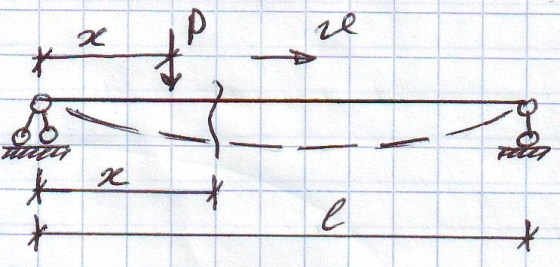
Задача Крылова.

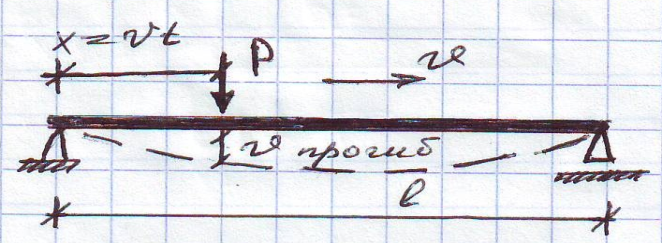EI=const; m=const

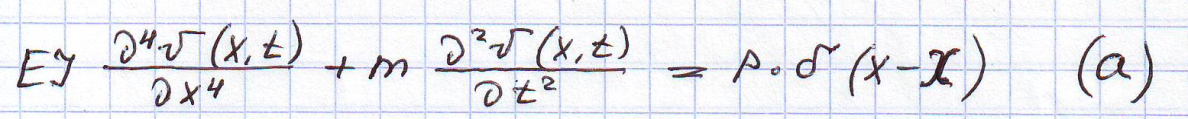
Это уравнение 2-го порядка решается методом разделения переменных по правилу Коши.

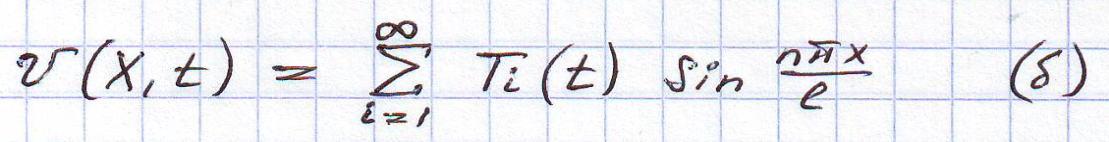
Подставим (б) в (а), а затем выполним преобразование уравнения путём его интегрирования в пределах длины балки после умножения на одну из собственных форм.

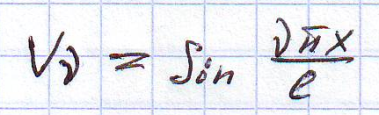собственная форма.

При этом учитывается, что собственные формы между собой ортогональны, уравнение становится такого вида:

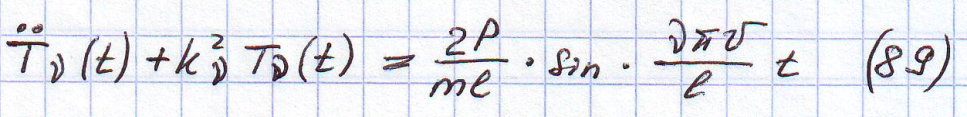
частота возмущения.

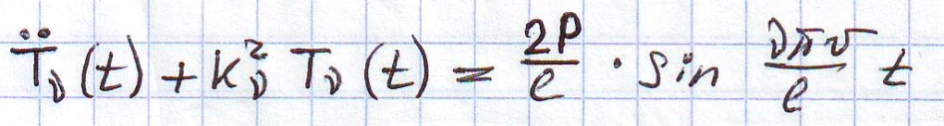
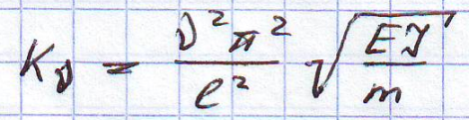частота собственных колебаний балки.

Полученная система уравнений представляет собой независимую систему д.у. 2-го порядка с правой частью. Решение для этого уравнения складывается из свободных колебаний с собственной частотой и вынужденных колебаний с частотой возмущения.

Для определения А и В учтём начальные условия:

1)При t=0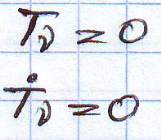

1.0=В*1 следовательно В=0

2.

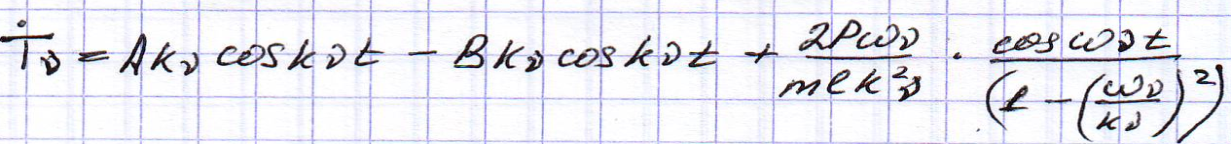
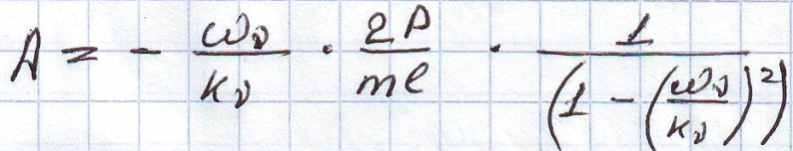
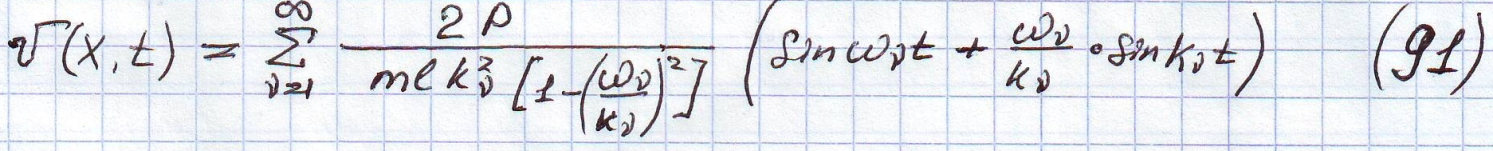
Проанализируем (91): при совпадении собственной частоты балки с частотой возмущения амплитуды возмущений растут, следовательно при движении нагрузки возможны критические скорости, при которых балка может получать большие перемещения.

Вычислим критическую скорость движения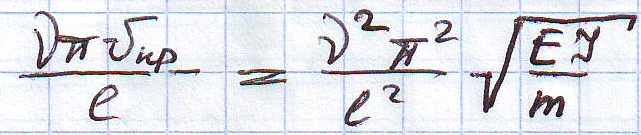

При

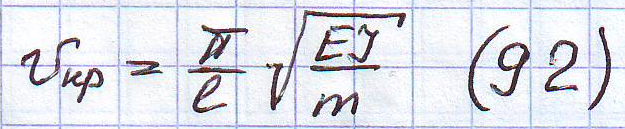
Пример:

Вычислим критическую скорость для моста с м

Приближенно для широкого класса мостовых сооружений период низшей собственной формы равен:

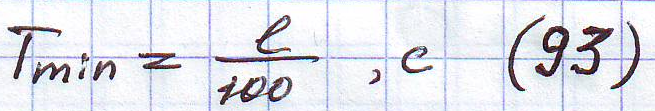
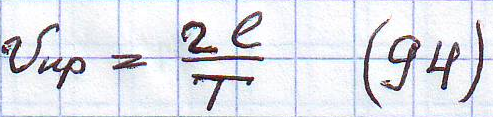
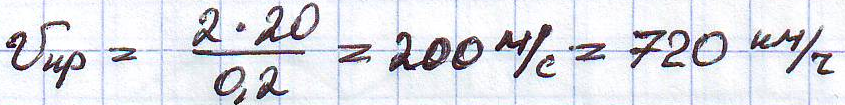
Для реальных скоростей движения критические скорости недостижимы.

Колебание неинертной балки при движении по ней инертного груза.

Задача Виллиса-Стокса.

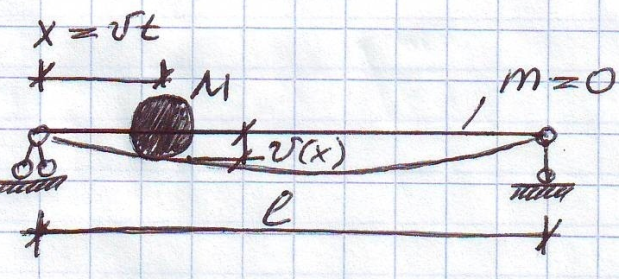
По условию задачи инертный груз движется по траектории, которая определяется прогибом балки под местным опиранием груза.

Давление груза на балку складывается из собственного веса и центробежного ускорения при движении по криволинейной траектории.

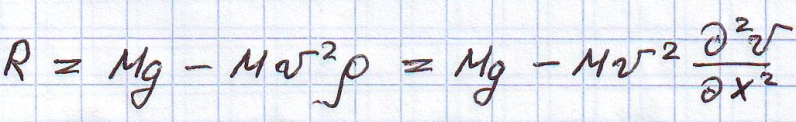
Прогиб в производном сечении балки в соответствии с такой постановкой определяется по формуле:

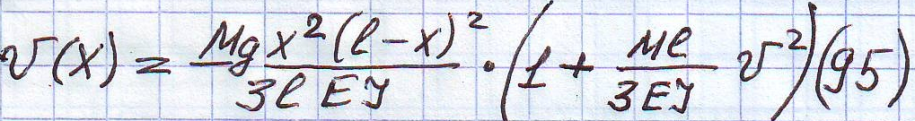
2 слагаемое в скобках представляет собой динамический эффект от движения по криволинейной траектории и представляет собой динамический коэффициент:

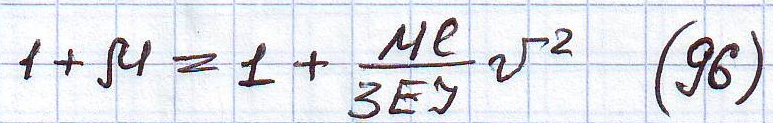
Пример: оценим величину динамического коэффициента при реальных скоростях движения.

Выпуск 56 СДП:

L=16,67m; EI=12 кН ; М=80т

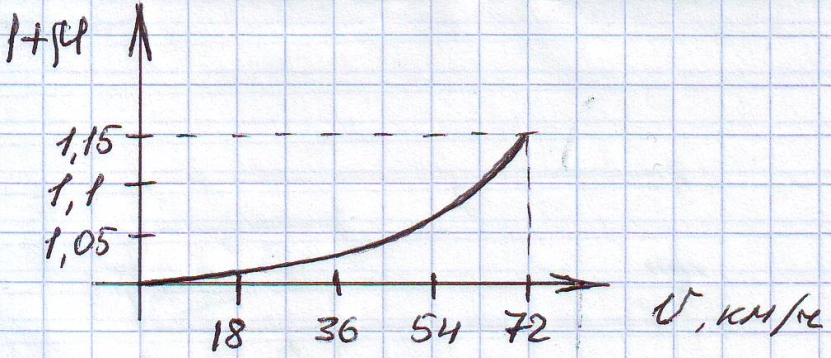
Движение инертного груза по инертной балке.

Задача Инглиса-Болотина.

При учёте инертности груза и балки, давление на балку будет определяться аналогично задаче Виллиса-Стокса:

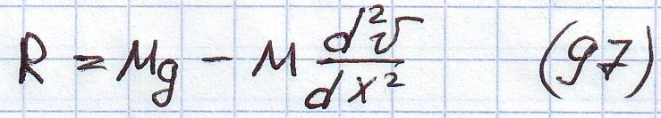
Но при вычислении ускорений учитывается полная производная перемещений по координате

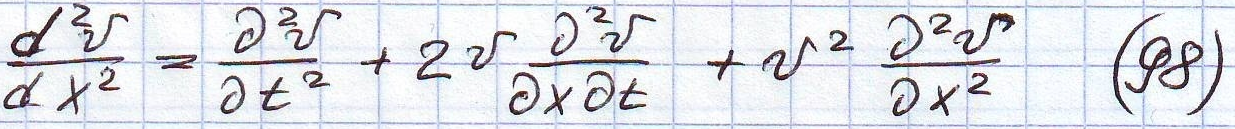
Из (98) 1-е слагаемое ускорение поступательного вертикального движения;

2-е слагаемое ускорение Кориолиса;

3-е слагаемое центростремительное ускорение.

В такой постановке аналитических решений, удобных для практического решения не существует.

Имеются численные исследования влияния отдельных слагаемых формулы(98).Они показывают, что ускорение Кориолиса изменяет величину давления в пределах 5-7%. Основное 1-е слагаемое.

Движение подрессорного груза по инертной балке.

Задача Моргаевского.

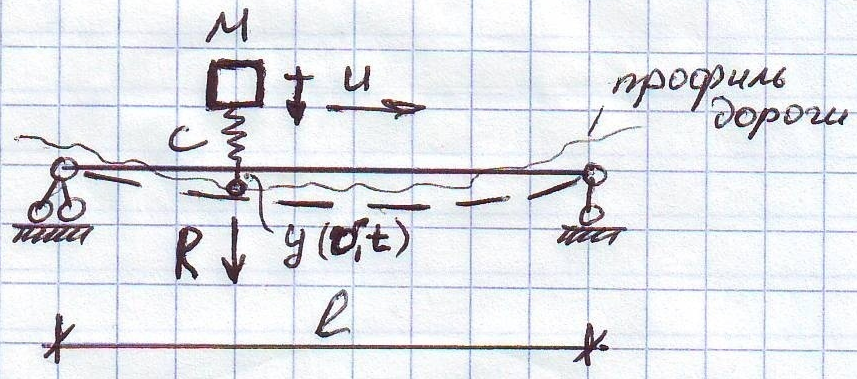
Y (τ,t) – прогиб под грузом

h (τ,t) – профиль дороги

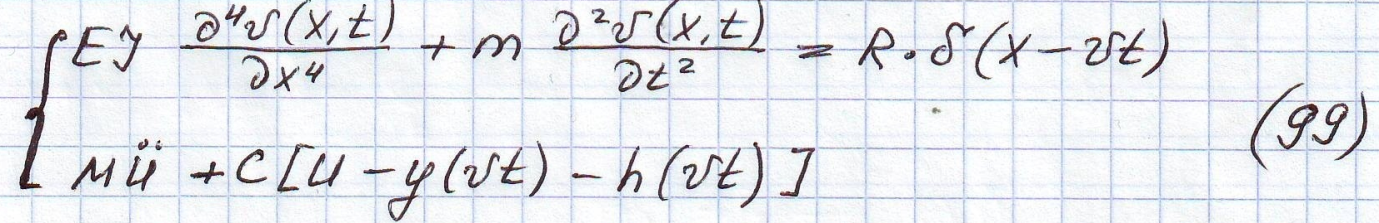
Описание колебаний балки совместно с движущемся грузом производится системой д.у. для подсистемы «мост» и подсистемы «автомобиль»; при этом учитывается «обратная связь» в системе, т.е. влияние колебаний моста на колебания автомобиля.

Лекция №16