В ынужденные колебания системы с бесконечным числом степеней свободы при произвольном силовом возмущении

Силовое воздействие является сосредоточенным на расстоянии, а от левой опоры и имеет произвольный закон изменения во времени, т.е. оно может быть импульсным, гармоническим и т.д.

(84)

каждое слагаемое левой части уравнения представляет собой интенсивность распределенной нагрузки.

Ф ункция Дирака.

фильтрующее свойство функции Дирака.

(84) – уравнение вынужденных колебаний балки при сосредоточенной нагрузке.

Уравнение в частных произведениях с двумя переменными x и t. Его решение возможно, если произвести разделение переменных по правилу Коши:

(a)

Такое представление называется разложением решения задачи в ряд по собственным формам. Подставляя (а) в (84) и интегрируя его в пределах длины балки после умножения на одну из собственных форм можно получить систему независящих обыкновенных Д.У.

(85)

i = 1, 2,…∞ a – расстояние определяющее положение силы

Такая система уравнений легко решается в аналитической форме, если правая часть представлена аналитическим выражением (например sin или еⁿ)

Колебания системы с 1-ой степенью свободы при произвольном возмущении. Интеграл Дюамелля.

Представляем возмущение в виде набора мгновенных импульсов

Импульс

Воспользуемся теоремой об изменении количества движения:

Изменение количества движения за заданный промежуток времени равен импульсу силы.

(a)

Для описания решения после воздействия одного из импульсов необходимо воспользоваться уравнением свободных колебаний:

Решение уравнения свободных колебаний известно:

A и β находятся из начальных условий:

1. при τ = 0 , u = 0

2. при τ = 0 ,

0 = А*sinβ

т.к. cos(kt)=1 то А

(86)

К олебания системы после воздействия мгновенного импульса

Для вычисления полного перемещения системы от произвольного возмущения формулу (86) необходимо поставить интеграл, который суммирует все свободные колебания после импульса.

(87)

Интеграл Дюамелля дает решение только вынужденных колебаний при движении возмущения. Для полноты описания дополнительно необходимо учесть сопровождающие свободные колебания. В приведенной форме не учитывается внутреннее трение. Для его учета достаточно в подынтегральное выражение ввести сомножитель

Лекция № 15

Колебания мостовых конструкций при подвижной нагрузке.

При движении автомобилей по мостовым конструкциям возникают колебания, причиной которых является наличие скорости.

Постановки задачи расчёта зависят от учёта инертности мостовой конструкции и инертности подвижной нагрузки.

1)Инертность нагрузки и мостовой конструкции не учитывается, а учитываются только фактические движения.

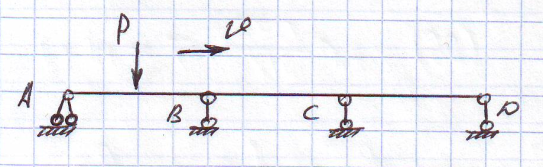
Эта задача рассматривается в статике сооружении с использованием линий влияния

2)Инертность мостовой конструкции учитывается, а подвижной нагрузки не учитывается(задача А.Н.Крылова).

3)Инертность нагрузки учитывается, а мостовой конструкции не учитывается.

(Задача Виллиса-Стокса)

4)Инертность нагрузки и мостовой конструкции учитываются.

(Задача Инглиса-Белотина)

5)Учитывается инертность нагрузки и мостовой конструкции, а для нагрузки учитывается её подрессоренность (упругое опирание на дорогу).

(Задача Моргаевского)