
- •Введение в динамику сооружений.
- •Основные понятия динамики сооружений.
- •Определение момента инерции абсолютно твердых тел.
- •Понятие о динамической расчетной схеме.
- •Понятие коэффициента жесткости для систем с 1 степенью свободы.
- •Определение и при последовательном и параллельном соединении упругих связей.
- •1)Прямая форма:
- •3) Силы неупругого сопротивления (силы трения).
- •4) Силы возмущения.
- •1) Внешние:
- •2) Силы инерции:
- •3) Силы неупругого сопротивления (трения).
- •Вынужденные колебания системы с 1 степень свободы при наличии силового гармонического возмущения.
- •Вынужденные колебания при наличии сопротивления.
- •Виброизоляция.
- •Решение д.У. Для колебаний системы с 1 ст. Свободы при переезде через неровность.
- •Теория Вибрографа
- •Обработка данных измерений динамичных параметров
- •Дифференциальные ур-я движения систем с конечным числом степеней свободы.
- •Д.У. Движения систем с n степенями свободы в обратной форме.
- •Свободные колебания систем с конечным числом степеней свободы.
- •Нормирование собственных форм упругой системы.
- •Проверка ортогональности собственных форм динамической системы.
- •Понятие о парциальных системах и парциальных частотах динамической системы.
- •Динамические модели автомобилей в виде систем с конечным числом степеней свободы.
- •Матрица жесткости 2х массовой модели автомобиля.
- •Переезд 2х массовой модели через неровность.
- •Переезд двух массовой модели через неровность.
- •Расчет динамического давления при переезде неровности системы с конечным числом степени свободы.
- •Определение критических скоростей движения автомобиля через неровность.
- •Динамические модели современных автомобилей.
- •1) Трехосный автомобиль с балансированной тележкой.
- •2) Сдельный автопоезд
- •Вынужденные колебания систем с конечным числом степ. Свободы при силовом гармоническом возмущении.
- •Теория виброгашения
- •К прочностному динамическому расчету систем с одной степенью свободы. Прямая форма уравнения движения.
- •Обратная форма уравнения движения
- •Теория устойчивости мостовых конструкций
- •Устойчивость сжатых стержней
- •Устойчивость плоской формы изгиба.
- •Деформационный расчет рамы для определения потери устойчивости второго рода.
- •Расчет устойчивости сс при определении критической силы при потере устойчивости 2го рода.
- •Р асчет устойчивости с.С. Для определения критического состояния 1го рода.
- •Определение формы потери устойчивости.
- •Учет симметрии при расчете устойчивости с.С.
- •Расчет с.С. С использованием сжато-изогнутых рам.
- •Энергетический метод определения нагрузок.
- •Устойчивость прямоугольной пластинки подвергающейся воздействию сжимающих сил.
- •Устойчивость плоской формы изгиба тонкостенных высоких балок.
- •Устойчивость плоской формы изгиба двутавровой балки.
- •Устойчивость арочных конструкций.
- •Расчет двух шарнирной арки.
- •Бесшарнирная арка
- •Трехшарнирная арка
- •Алгоритм определения критических нагрузок на мостовые сооружения с использованием современных конечно-элементных комплексов.
- •Свободные колебания систем с бесконечным числом степеней свободы
- •В ынужденные колебания системы с бесконечным числом степеней свободы при произвольном силовом возмущении
- •Колебания системы с 1-ой степенью свободы при произвольном возмущении. Интеграл Дюамелля.
- •Колебания мостовых конструкций при подвижной нагрузке.
- •Задача Крылова.
- •Колебание неинертной балки при движении по ней инертного груза.
- •Движение инертного груза по инертной балке.
- •Движение подрессорного груза по инертной балке.
- •: Основы расчета упругих систем на сейсмические воздействия.
- •Современные методы расчета зданий и сооружений на сейсмические воздействия.
- •Распространение волн в упругих средах.
- •Воздействие вибрации на людей.
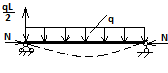
Устойчивость плоской формы изгиба.
2)
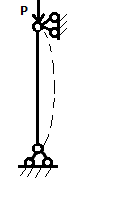
 При
превышении силы Ркр
возникает криволинейная форма равновесия,
при которой изгиб справляется с
загружением.
При
превышении силы Ркр
возникает криволинейная форма равновесия,
при которой изгиб справляется с
загружением.
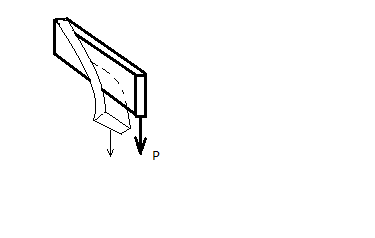
В двух задачах рассматриваемых в курсе сопротивления материалов о сжатии стойки и изгибе балки общими являются резкая смена видов напряженного состояния при достижении значения силы критической вершины.
В первом случае наряду со сжатием появляется изгиб, а во втором - с изгибом – кручение.
Момент смены видов напряженного состояния называется бифуркацией (2 формы).
Такое явление в строительной механике называется потерей устойчивости первого рода.
Наряду с этим видом потери устойчивости можно рассматривать потерю устойчивости второго рода, когда в конструкции нарастает деформируемое состояние скачком или резким изменением жесткости.
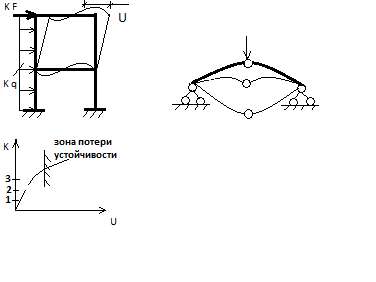
К – параметры изменения нагрузки.
В простейшем случае К одинаково для всех нагрузок – простое состояние.
Деформационный расчет рамы для определения потери устойчивости второго рода.
поперечный изгиб
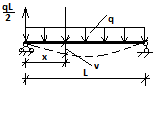
EJV"
= ± M =
 x –
x –

продольно-поперечный изгиб
 EJV"
=
x –
+
NV
EJV"
=
x –
+
NV
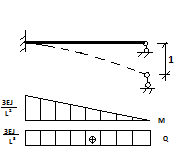
Деформационный расчет рамы можно осуществить на основе метода перемещений, для которого должны быть использованы уточненные таблицы защемленных балок на воздействие единственных перемещений, которое учитывают влияние нормальных сил.
Рассмотрим одно из табличных состояний защемленной балки.
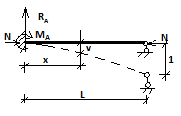 EJV"
= ± M = - (MA
+
RAx
+NV)
EJV"
= ± M = - (MA
+
RAx
+NV)
V"
+
 V
=
V
=
 (-
MA-
RAx)
(-
MA-
RAx)
Имеем неоднородное д. у. второго порядка, с постоянными коэффициентами, для которого решение:
VOH = VOO + VЧН
n2 =
V" + n2 V = (- MA- RAx)
VOO = C1cos n x + C2 sin n x
VЧН = Д + Е х
С1; С2; Д; Е – постоянные интегрирования
V' = E
V" = 0
n2
(Д
+ Ех)
=
(- MA-
RAx)
=>Д
= -
E
= -

V
= C1cos
n x + C2
sin n x -
-
 (a)
(a)
V' = - C1 n sin n x + C2 n cos n x -
при х = 0; V = 0
0 = C1n - =>C1 = (б)
при х = 0; V' = 0
0
= С2n
-
=>C2
=
 (в)
(в)
(б) и (в) → в (а)
V
=
 + RA
+ RA
V'
= - MA + RA
+ RA
V"
= - MA - RA
- RA
M = - EJV" = MAcos n x + RA sin n x
Постоянные МА и RAопределили из граничных условий на правом конце.
При х = L → V = 1
1 = + RA
При х = L → M =0 или V" =0
0 = MA*cos n L + RA sin n L
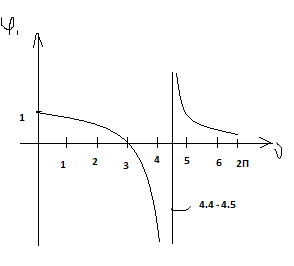
Решая эти уравнения относительно МА и RA получим, введя следующие обозначения:
ν=
nL = L (7)
(7)
MA
=
-
 *
* = -
*ϕ1
(ν)
(8)
= -
*ϕ1
(ν)
(8)
RA=
 *
* =
*η1(ν)
(9)
=
*η1(ν)
(9)
 Таблицы
защемленных балок с учетом продольной
силы являются корректирующими таблицы
защемленных балок без N.
Таблицы
защемленных балок с учетом продольной
силы являются корректирующими таблицы
защемленных балок без N.
В них допущения учитываются с помощью специальных функций ϕi(ν) влияние N.
Для Q корректировка ведется с помощью функций ηi(ν) .
Лекция № 11
Расчет устойчивости сс при определении критической силы при потере устойчивости 2го рода.
Этот расчет основан на описанном выше деформационном расчете с введением этих же допущений.
Он состоит в вычислении деформационного состояния рамы в зависимости от величины нагрузки.

кq
При расчете деформационного состояния системы значение параметра К

Критическое
воздействие PH
определяется:
 (10)
(10)
В
качестве
 - усилия, напряжения, перемещения и
т.д.
- усилия, напряжения, перемещения и
т.д.
