Лекция №1

Введение в динамику сооружений.

Динамика сооружений – это раздел строительной механики который посвящен изучению метода расчета деформируемых тел на нагрузки, изменяющиеся во времени (динамические нагрузки)

Классификация нагрузок.

Нагрузки делятся на две большие группы:

1. Силовые воздействия

2. Кинетические воздействия

По характеру воздействия 1 и 2 могут быть:

1. Гармонические (моногармонические, полигармонические)

2. Апериодические

3. Импульсные

4. Случайные (неровности на дороге)

Основные понятия динамики сооружений.

Масса - это мера инертности тела при поступательных движениях

1Н= 1 кг×м/с² 1кН=1 Т*м/с²

P=M×g M=

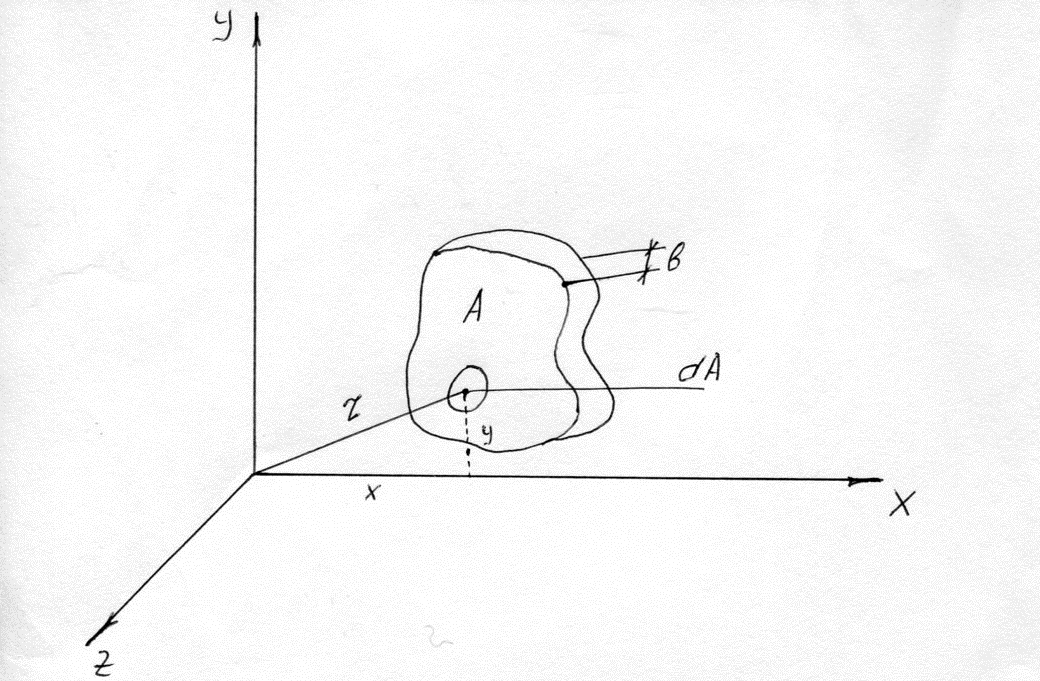
Определение момента инерции абсолютно твердых тел.

Момент инерции – это мера инертности тела при вращательном движении. ²dm (кГ×м²; Т×м²)

dm – масса 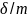элемента тела

r – расстояние до оси вращения

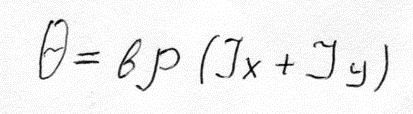(2)

При вычислении момента инерции для различных осей фигур можно использовать формулу:

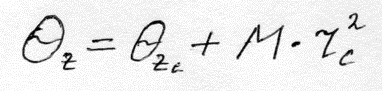(3)

Пример:

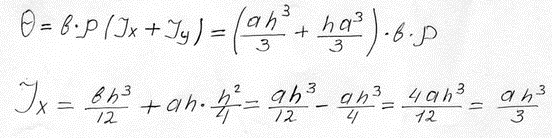
При вычислении момента инерции тел достаточно сложной формы используются экспериментальные методы, при которых изучают поведения тела после заданного воздействия и выполняют расчеты для вычисления моментов инерции.

Понятие о динамической расчетной схеме.

Под понятием расчетной динамической схемой понимается схема расположения совокупности инертных элементов системы, при расчетах на динамические воздействия.

Динамическая расчетная схема классифицируется в зависимости от числа степеней свободы, которое определяется положением инертных элементов в плоскости или пространстве в любой момент времени.

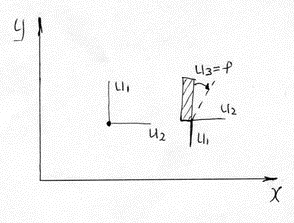
Сосредоточенная масса имеет в плоскости 2 степени свободы, а в пространстве 3 степени свободы.

Тело определенных размеров в плоскости имеет 3 степени свободы, а в пространстве 6.

По числу степени свободы расчетная схема динамического сооружения классифицируется на:

1. Системы с 1 степенью свободы

2. Системы с конечным числом степени свободы

3. Системы с бесконечным числом степени свободы

Пример:

1 степень свободы

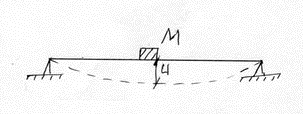
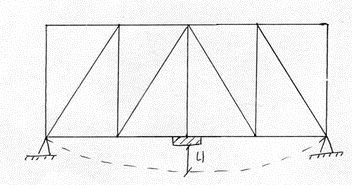
2 степени свободы.

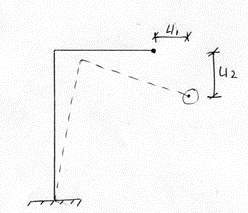
Для моделирования систем с одной степенью свободы применяется универсальная модель в виде груза на пружине

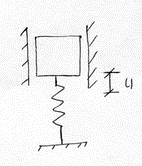с 1 степенью свободы.

Для оценки жесткости и податливости упругой связи поддерживающий инертный элемент применяется 2 понятия:

1. Коэффициент податливости ( )

2. Коэффициент жесткости (с)

с – коэффициент жесткости упругой связи – это величина силы или пары сил которую необходимо приложить к инертному элементу, чтобы вызвать его единичное перемещение линейное или угловое.(Н/м; Н*м/рад)

коэффициент податливости – это величина перемещения линейного или углового которое возникает при приложении к инертному элементу единичной силы или пары сил. (м/Н; рад/Н*м)

Коэффициент податливости определяется из формулы Мора:

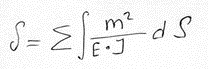(4 ) – изгибаемые конструкции.

m – эпюра моментов от единичного воздействия по направлению податливости искомой связи.

Конечное число степеней свободы.

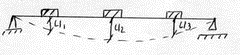
(i=1,2,3….n)