Буковинський університет

Факультет комп’ютерних систем і технологій

Курсовий проект (робота)

з комбінаторної оптимізації

на тему: «Методи розв’язування задач стохастичного програмування»

студента IV курсу К-401 групи Дуки Євгенія напряму підготовки 6.050101 «комп’ютерні науки» Керівник: доцент кафедри вищої математики та природничих дисциплін, доцент, кандидат фіз.-мат.наук, Нікітін А. В. Національна шкала_____________ Кількість балів: Оцінка: ECTS_____ ________ _______________ (підпис) (прізвище та ініціали) ________ _______________ (підпис) (прізвище та ініціали) ________ _______________ (підпис) (прізвище та ініціали)

Члени комісії

м.Чернівці – 2013

ЗМІСТ

Вступ Розділ 1. Стохастичні квазіградієнтні методи.

Задача 0. Знайти arg min max Etp (x, у, со) для заданої функції f₀ : Rn X Rm X Q ->- R1 й заданої множини X cz Rn.

Припущення 0. (i) — функція, f₀ опукла до низу, (іі) – множина Х опукла і замкнута.

Стохастичні квазіградієнтні методи застросовуються для розв’язування задач оптимізації, у яких немає достатньо повної інформації про цільову, функцію, функції обмежень та їх похідні. Ці методи основані на понятті стохастичного квазіградієнта - випадкового вектора який задовольняє рівність:

Е{£1х\...,х^к) = а_к%(х^к)+Ъ^к,

де а_к - невід'ємна випадкова величина, b^к - випадковий вектор, вимірні відносно <7 –підалгебри, індукованої сімейством випадкових величин ( ,.... ); f₀ ( ) – узагальнений градієнт функції ф₀ в точці . Наведемо приклад обчислення стохастичних квазіградієнтів для функції f₀.

1. Приклади обчислення стохастичних квазіградієнтнів.

Нехай функція f₀(х) має обмежені другі похідні. Розглянемо вектор β = (β _1,.... β_n) ^Т з незалежними й рівномірно розподіленими на [-1;1] компонентами. Тоді вектор стохастичного квазіградієнта на к -й ітерації можна обчислювати за формулою:

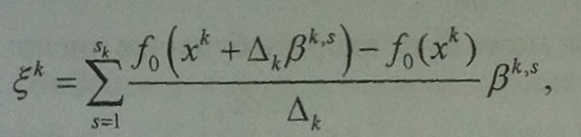
де β ^{k s} , s = 1, S_k - серія незалежних спостережень β на k – ітерації. Якщо випадкові величини вимірні відносно α – підалгебри β_к , індукованої величинами х⁰,…,х^k, то умовне математичне сподівання такого вектора дорівнює:

де – v^k деякий випадковій вектор, вимірний відносно β_к , ||v^k|| < const.

2. Методи проектування стохастичних квазіградієнтів.

Алгоритм 1.

Початок 1. Вибрати довільну початкову точку x⁰ є Rⁿ , для якої ∑||x⁰|| < ∞ ; задати послідовність крокових множників {p^k}^∞_k=0 і послідовність нормуючих множників {y_k}^∞_k=0 .

2. Покласти k = 0.

3. Осносний цикл. Обчислити реалізацію випадкового вектора £^к(w), умовне математичне сподівання якого :

Е(£^к/х° х^к) = а_кУf₀(х^к)+Ь^к,

де а_к – невід’ємна випадкова величина й b^k(b^k_1,…..,b^k _n)^T - випадковий вектор, який залежить від послідовності x⁰,….,x^k.

4. Обчислити вектор.

5. Покласти к = к + 1 і перейти на крок 3.

Теорема 1. Нехай виконується припущення 0 і нехай існують такі постійні β і A , що:

f₀(x)>f₀(x^*)+ β||x^*-x||²

при х є Х, і з ймовірністю 1:

∑(||£^k||²/x⁰,….,x^k)<A

Крім цього, р^к детерміновані та:

a_k>a>0, ||b^k||<r_k , r_k < p_k , r_k < r < 2βa.

Тоді існує таке число c_k < const , що при p_k = c_k / k послідовність {x^k}^∞_k=0 із ймовірністю 1 збігається до єдиного розв’язку х^* , причому

∑||x^*-x^k|| = O(1/k).