12. Різницеві методи чисельного розв’язання багатовимірних задач Математичної фізики. Різницева схема звагами для дво вимірного рівняння теплопровідності.

1. Постановка задачі.

Нехай в області є {0<x1<ℓ1

0<x2<ℓ2}, що являє собою прямокутник з сторонами ℓ1 та ℓ2 , межею Г на проміжку часу [0,T] .

Розглянемо першу крайову задачу для двовимірного рівняння теплопровідності:

, (x1,x2,t) є Ω (1)

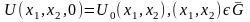(2)

, 0<t≤T (3)

(3')

В курсі математичної фізики доводиться, що сформульована перша крайова задача (1)-(3) поставлена коректно для достатньо гладких крайових умов (1)-(3).

2. Різницева апроксимація задачі (1)-(3)

Для побудови РС задачі (1)-(3) введемо різницеву сітку таким чином:

1.Просторову сітку

Множину внутрішніх вузлів сітки в Ω (і=1,n-1, j=1,m-1) позначимо через ω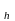 і назвемо внутрішніми вузлами просторової сітки ω . А множину вузлів сітки Ω є Г називають межовими вузлами сітки і позначають через γ . Отже Ω

Оператор Лапласа в (1) апроксимуємо на п’ятиточковому шаблоні ’хрест’ п’ятиточковим різницевим оператором

Визначимо на Ω різницевий оператор

На введеній вище просторовій Р сітці , позначивши апроксимуємо задачу (1)-(3) різницевою задачею , в результаті чого отримаємо ,по аналогії з одновимірним випадком , так звану РС звагами:

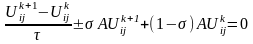, i=1,n-1, j=1,m-1, k=1,k-1 (4)

(5)

, k=1,K (6)

Схема (4)-(6) називається РС звагами .

Для одновимірного рівняння теплопровідності аналогічна схема звагами мала вигляд:

Умова стійкості даної схеми мала вигляд σ ≥ ½-¼γ.

Аналіз схеми (4)-(6)

1. При σ =0 отримаємо явну РС, а саме

(8)

(9)

(10) k=1,K

З (8) легко отримаємо

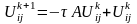(8')

i=1,n-1, k=1,k ,j=1,m-1 (8")

2.При σ0, схема (4)-(6)- неявна і для знаходження U на (К+1) шарі потрібно розв’язати систему двовимірних різницевих рівнянь. Ця схема , в силу побудови має порядок апроксимації 0(h²+τ). А при σ =0.5- дана РС має порядок апроксимації 0(h²+τ²).

3.Стійкість РС.

Розглянемо лише стійкість РС (4)-(6) у початкових даних. Дослідження стійкості проводиться, по аналогії , як і у одновимірному випадку за допомогою методу розділення змінних. В теорії РС показується (див. Самарський) , що РС навіть більш загальний вигляду ніж (4)-(6) стійка по почат. Даних, якщо ваговий множник σ задовольняє умова:

(11)

τ-крок по часу

λmax- це max власне значення верхньої межі спектра оператора А. Як відомо, для оператора А власне значення у нашому випадку має вигляд:

(12)

Можна показати, що

Тому умова стійкості (11) буде виконана , якщо ваговий множник σ задов. умові:

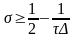(13)- аналог умови куранта

Аналогічно досліджується стійкість даної РС по правій частині та її збіжність. Якщо σ =0.5, то РС (4)-(6) має другий порядок точності по τ і по h. При решті σ –перший порядок точності по τ і другий – по h. У випадку квадратної РС умова стійкості (13) приймає вигляд:

(13')

У випадку явної РС (σ =0) для квадратної сітки умова стійкості набуває вигляду τ/h²≤¼.

Ця умова ще більш жорсткіша , ніж в одновимірному випадку.

Як ми бачили . у випадку σ 0, ми отримали неявну РС і для її розв’язання потрібно було розв’язувати систему двовимірних різницевих рівнянь. Однак, це не так просто , тобто наштовхується на значні труднощі. Тому в теорії РС різними шкалами були розроблені так звані економічні методи побудови і розв’зання РС.