К госэкзамену по химии (д/о, 4 курс, магистры по кафедре физической химии) Вопросы

1. Ион-дипольное взаимодействие в растворах электролитов. Сольватация и гидратация

2. Теоретическая интерпретация электропроводности электролитов (гидродинамическая теория, теория Дебая – Онзагера, кинетическая и прототропная теории)

3. Классификация электродов. Электроды первого и второго рода, газовые электроды, амальгамные электроды, окислительно-восстановительные электроды, правило Лютера. Применение электродов

4. Неравновесные электродные процессы. Электродная поляризация, перенапряжение. Теория электрохимического перенапряжения Эрдей-Груза и Фольмера

5. Реакция катодного выделения водорода: опытные закономерности, возможные стадии реакции, механизм водородного перенапряжения на различных металлах

6. Анодное растворение металлов

7. Реакция катодного выделения металлов: общая характеристика процесса, роль природы металла и состава раствора. Природа металлического перенапряжения. Особенности катодного образования поликристаллических осадков

1. Ион-дипольное взаимодействие в растворах электролитов.

Сольватация и гидратация Недостатки теории электролитической диссоциации Аррениуса

В качестве одной из количественных характеристик электролита теория Аррениуса предлагает степень электролитической диссоциации , определяющую долю ионизированных молекул в данном растворе. В согласии с ее физическим смыслом  не может быть больше 1 или меньше 0; при заданных условиях она должна быть одной и той же, независимо от метода ее измерения (по измерению электропроводности, осмотического давления или ЭДС). Однако на практике значения , полученные разными методами, совпадают только для разбавленных растворов слабых электролитов; для сильных электролитов расхождение тем больше, чем больше концентрация электролита, причем в области высоких концентраций  становится больше 1. Следовательно,  не может иметь того физического смысла, который ей приписывался теорией Аррениуса.

Второй количественной характеристикой по теории Аррениуса является константа диссоциации; она должна быть постоянной для данного электролита при заданных Т и р, независимо от концентрации раствора. На практике только для разбавленных растворов очень слабых электролитов К_дис остается при разбавлении более или менее постоянной.

Таким образом, теория электролитической диссоциации приложима только к разбавленным растворам слабых электролитов.

Существенным недостатком теории Аррениуса является и то, что она не указывает причин, вызывающих ионизацию электролитов в растворах. Термин «электролитическая диссоциация» подразумевает образование ионов в растворе при распаде нейтральных молекул растворяемого вещества. Однако часто ионы существуют уже до растворения: кристаллы солей построены из ионов, и при растворении должно произойти разрушение кристалла. Расчеты энергии кристаллической решетки G_p (энергия кристаллической решетки – это работа, которую нужно затратить для разрушения решетки, то есть для разведения составляющих ее ионов на бесконечно большое расстояние в вакууме) показывают, что количество термической энергии при обычных температурах слишком мало по сравнению с тем, которое надо затратить на разрушение решетки.

Одно из первых (и одно из наиболее точных) уравнений для подсчета энергии решетки – уравнение Борна (1918):

G_p = N_A ,

К_М – константа Маделунга, зависящая от характера взаимного расположения ионов в кристаллической решетке; ее значения известны для различных типов решетки;

r – равновесное расстояние между ионами противоположного знака в данном кристалле; обычно оно определяется по принципу плотной упаковки и отвечает сумме кристаллохимических радиусов;

n – константа, характеризующая изменение сил отталкивания с расстоянием между частицами; рассчитывается из данных по сжимаемости кристаллов; она лежит в пределах от 5 до 12;

Воспользуемся приведенными уравнениями для оценки энергии решетки NaCl, подставив численные значения. Формула Борна дает для энергии решетки

G_p = = 762 кДж/моль .

Как было показано Борном и Габером (1919), энергию решетки можно найти из термохимических данных, если воспользоваться циклом, основанным на законе Гесса. Подобный цикл можно составить для любого кристаллического вещества. Для NaCl цикл имеет вид:

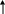NaCl _(кр) Na⁺_(газ) + Cl^–_(газ)

– е^– G_ион + е^– G_ср

Na _(газ) + Cl _(газ)

G_обр G_суб G_дис

Na _(тв) + ½ Cl_{2 (газ)}

G_обр – энергия образования хлорида натрия из элементарных натрия и хлора, взятых в их стандартных состояниях (твердый кристаллический натрий и газообразный молекулярный хлор);

G_суб – энергия сублимации натрия;

G_ион – энергия ионизации натрия;

G_дис – энергия диссоциации молекулярного хлора;

G_ср – энергия, характеризующая сродство электрона к газообразному атомарному хлору.

G_р = – G_обр + G_суб + G_ион + G_дис + G_ср =

– (– 384) + 78 + 496 + 203 – 387 = 774 кДж/моль .

Полученное значение достаточно хорошо согласуется с энергией решетки, подсчитанной по уравнению Борна.

В кристаллической решетке соседние ионы Na⁺ и Cl^– по сравнению с изолированной молекулой NaCl обладают меньшим числом степеней свободы, поэтому тепловую энергию молекулы NaCl можно рассматривать как ее максимальное значение для пары противоположно заряженных ионов в решетке. Свободная молекула NaCl обладает семью степенями свободы, то есть при 298К запас ее тепловой энергии составляет 8,68 кДж/моль, из которой всего лишь около 2,5 кДж/моль приходится на колебательную энергию, непосредственно вызывающую распад молекул. Это количество термической энергии слишком мало по сравнению с тем, которое надо затратить на разрушение решетки (762 кДж/моль), чтобы обеспечить сколько-нибудь заметную диссоциацию хлорида натрия на ионы. В то же время известно, что в водном растворе NaCl   1.

Наиболее полная и четкая формулировка основных недочетов теории Аррениуса и путей их преодоления дана в трудах Д.И.Менделеева. Причина всех недостатков теории заключается в игнорировании взаимодействия частиц растворенного вещества между собой, а также с молекулами растворителя. Менделеев отмечал, что для растворов существенны не только процессы диссоциации, но и процессы образования новых соединений с участием молекул растворителя.

В теории Аррениуса ионы рассматривались как частицы идеального газа, а следовательно, не учитывались обусловленные кулоновскими силами притяжение катионов и анионов и отталкивание одноименно заряженных ионов. Пренебрежение ион-ионным взаимодействием, совершенно непонятное с физической точки зрения, и приводило к нарушению количественных соотношений теории Аррениуса, о чем уже говорилось выше (константа диссоциации не оставалась постоянной, а изменялась при изменении концентрации электролита, что особенно отчетливо проявлялось в растворах сильных электролитов – так называемая «аномалия сильных электролитов»; различные методы определения степени диссоциации  давали несовпадающие результаты, а в концентрированных растворах сильных электролитов иногда получались не имеющие физического смысла значения   1 и др.).

Если в раствор ввести большой избыток постороннего электролита (так называемого «фона»), который не участвует непосредственно в ионных равновесиях, то в этих условиях основные соотношения теории Аррениуса выполняются с очень хорошей степенью приближения. Метод введения избытка индифферентного электролита был предложен Я.Брёнстедом и получил название метода постоянной ионной среды.

Если игнорировать ион-дипольное взаимодействие (то есть взаимодействие ионов с диполями воды или другого растворителя), то нельзя объяснить процесс образования ионов и устойчивость ионных систем, ведь именно это взаимодействие, как показано далее, является физической основой образования ионов в растворе при растворении электролита. Вопрос о причинах электролитической диссоциации вскрывает наиболее уязвимые места теории Аррениуса.