2. Метод Гаусса – Жордана

Исходные уравнения:

;

Далее работаем над вторым столбцом:

Далее работаем над третьим столбцом:

4. Методы оптимизации

З

адача 2

Н1

Н2

U1

U2

Первый шаг: в качестве свободных элементов выбираем

Базисное решение

Шаг второй: в качестве свободных элементов выбираем

Базисное решение

Третий шаг: в качестве свободных элементов выбираем

U1

U2

Н1

Н2

3. Теория вероятности в задачах электроснабжения

З

адача 5

Коэффициент корреляции

;

Решение:

Определим нагрузку на угловом участке I.

Математическое ожидание тока на первом участке:

Дисперсия и среднеквадратичное отклонение на головном участке I:

Аналогично определяем нагрузку на втором головном участке:

Дисперсия:

Задача 6

В течение периода зимнего максимума нагрузки трансформаторов моделируются системой независимых случайных величин и числовыми характеристиками .

600	700	300	400	500	450	150	250

200	150	100	150	150	100	80	90

Взаимосвязь между режимами электропотребления характеризуется коэффициентами корреляции

Определим числовые характеристики нагрузки на пятом участке. Нагрузка включает в себя линию и трансформатор.

Определим дисперсию нагрузки на 5 участке:

Среднеквадратичное отклонение

Определим расчётное значение нагрузки на пятом участке, вероятность превышения которой

Коэффициент одновременности:

Характеристика нагрузки на первом участке линии:

Нагрузка на первом участке вероятность превышения которой

Коэффициент одновременности:

Задача 7

Определим числовые характеристики нагрузки на V участке:

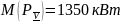, останется прежним.

Тогда:

И соответственно на первом участке:

Задача 3

	40	25	20	35	15

20	25	17	26	30	32	20	35	40

Решение: Нагрузка узлов (МВт):

Длины дуг графа (км): .

Линеаризованные дисконтные затраты на сооружение сети в тыс. руб/км могут быть вычислены по формуле:

Будем исходить из следующей математической модели:

.

Её развернутая функциональная форма:

;

;

Введём следующие обозначения:

С учётом этого:

Представим модель в канонической форме по Канторовичу.

Разрешим задачу отыскания наилучшего статического графа сети методом обратной матрицы. Первая итерация:

Сформируем матрицы и векторы :

Обратная матрицы от :

Определим базисные компоненты начального опорного плана:

Таким образом, предположения о базисных компонентах верны и начальный опорный план примет вид:

Проверим его оптимальность:

Вектор управления не является оптимальным, т.к. среди оценок имеются отрицательные. Введём в базис вектор поскольку он минимальный.

и найдём

Отсюда следует, что выводить из базиса необходимо вектор условий

Таким образом на второй итерации: ;

формируем матрицы и векторы :

;

Обратная матрица от : ;

Определим базисные компоненты нового опорного плана:

Очередной опорный план:

Проверим его оптимальность:

Вектор управления не является оптимальным, т.к. среди оценок имеются отрицательные. Будем выводить в базис вектор поскольку он минимальный.

Вычислим:

И найдём

Таким образом на третьей итерации ;

формируем матрицы и векторы :

; ;

Обратная матрица от

Определим базисные компоненты опорного плана:

Очередной опорный план: ;

Проверим его оптимальность:

План оптимален, т.к. среди оценок нет отрицательных.

Таким образом: .

С целью проверки и интерпретации полученных результатов обратимся к (2.10)