Билет 1
1)Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету
2)Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны
Св-ва:
1.В параллелограмме противоположные стороны равны и противоположные углы равны
2.Диагонали параллелограмма точкой пересечения делятся пополам
Билет 2
1)Два треугольника называются равными если их можно совместить наложением Признаки равенства треугольников:
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
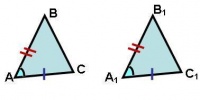
2.Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
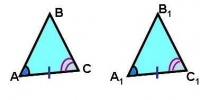
3.Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
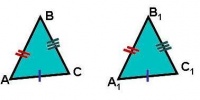
2)Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Теорема, обратная теореме Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный
Билет 3
1)Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
2)Ромб-это параллелограмм, у которого все стороны равны
Диагонали ромба взаимно перпендикулярны и делят его углы пополам
Билет 4
1)Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.
Признаки подобия треугольников:
1.Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
2)Равнобедренный треугольник - треугольник у которого 2 стороны равны
Св-ва равнобедренного треугольника:
1.В равнобедренном треугольнике углы при основании равны
2.В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
3.В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой
4.В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой
Билет 5
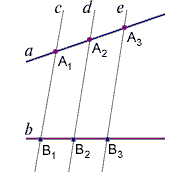
1)Теорема Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
2)Св-ва биссектрисы угла:
Луч исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла
Билет 6
1)Угол, верши на которого лежит на окружности, а стороны пересекают окружность, называется вписанным.
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Следствия из теоремы:
1.Вписанные углы, опирающиеся на одну дугу равны
2.Вписанный угол, опирающийся на полуокружность - прямой
2)Параллелограмм - четырехугольник, у которого противоположные стороны попарно параллельны
Признаки пар-ма:
1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник - параллелограмм 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм
Билет 7
1) Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки.
Формулы:
c=2πR c-длинна окружности,R-радиус окружности
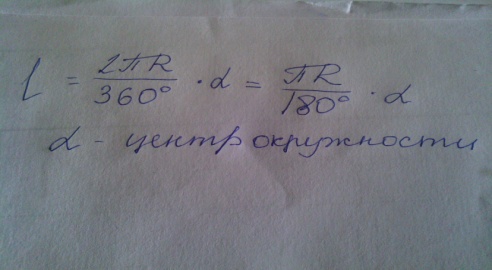
2)Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Св-ва средней линии треугольника:
1.Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Билет 8
1) Для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами: 1. Равные фигуры имеют равные площади; 2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей. 3. Площадь квадрата равна квадрату его стороны
2) Медиана треугольника – это отрезок, соединяющий вершину с серединой противолежащей стороны
Биссектриса треугольника - это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Билет 9
1)Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов выпуклого n-угольника равна (n-2)180º
2)Площадь треугольника равно половине произведения его основания на высоту.
Следствия из теоремы:
1.Площади прямоугольного треугольника равно половине произведения его катетов
2.Если высоты двух треугольников равны, то их площади относятся как основания
Билет 10
1)Проведем какой-нибудь луч АМ, не лежащий на прямой АВ, и на это луче отложим последовательно отрезки AC и CD,равные отрезкамP1Q1 и P2Q2.Затем проведем прямую BD и прямую, проходящую через точку С параллельно прямой BD. Она пересечет отрезок АВ в искомой точке Х
2)Две прямые на плоскости называются параллельными, если они не пересекаются
Признаки параллельности прямых:
1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то эти прямые параллельны.
2. Если при пересечении двух прямых секущей, соответственные углы равны, то эти две прямые параллельны.
3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Билет 11