- •Вопрос №2. Канал связи с точки зрения оти
- •Вопрос № 3. Определение понятия информация
- •Кроме этого информация обладает еще следующими свойствами:
- •Вопрос №4 виды источников сообщения: дискретная и непрерывная
- •Вопрос №5 критерии эффективности канала связи: пропускная способность, надежность, помехоустойчивость.
- •Вопрос №6 свойства информации. Понятность, полнота, массовость, интерпретируемость, достоверность
- •Вопрос №7 классификация информации по различным критериям.
- •Вопрос № 8 входная, выходная, внутрисистемная информация
- •Вопрос № 9 исходная, результирующая информация. Дискретная, непрерывная информация
- •Вопрос № 10 информационные процессы
- •Вопрос № 11 информация в живой природе
- •Вопрос № 16 информационное общество. Информатизация общества
- •Вопрос № 17 энтропия как мера неопределенности выбора
- •Вопрос № 20 правила определения энтропии по Шеннону
- •Вопрос № 22 метод половинного деления
- •Вопрос № 23 основные свойства энтропии. Информационная энтропия источника и термодинамическая энтропия
- •Вопрос № 24 содержательный подход к количественному измерению информации
- •Вопрос № 26 компьютер- универсальное средство обработки информации
- •Вопрос № 27 представление числовой информации в компьютере. Форма с фиксированной точкой
- •Вопрос № 28 пердставление числовой информации. Форма с плавающей точкой
- •Вопрос № 29 представление символьной информации в памяти компьютера
- •Вопрос № 30 представление графической информации в памяти компьютера
- •Вопрос № 31 растровое представление
- •Вопрос № 33 представление звуковой информации
- •1000 Измерений за 1 секунду — 1 килогерц (кГц).Характерные частоты дискретизации аудиоадаптеров: 11кГц, 22 кГц, 44,1 кГц и др.
- •Вопрос № 34 системы счисления. Позиционные и непозиционные
- •Вопрос № 35 позиционные системы счисления
- •Вопрос № 36 алгоритм перевода целых десятичных чисел в кратные системы счисления
- •Вопрос № 39 восьмеричная система счисления
- •Вопрос № 40 шестнадцатиричная система счисления
- •Вопрос № 41 арифметика в позиционных системах счисления
Вопрос № 28 пердставление числовой информации. Форма с плавающей точкой
Обработка
очень больших и очень маленьких чисел
производится в экспоненциальной форме.
В этом случае положение запятой в записи
числа может изменяться. Поэтому
представление в памяти чисел в
экспоненциальной форме называется
представлением с плавающей точкой
(запятой). Любое число А в экспоненциальной
форме представляется в виде:
А
= mА ![]() qp,
где
mA -
мантисса числа, q - основание системы
счисления, p - порядок числа.
Для
однозначности представления чисел c
плавающей точкой используется
нормализованная форма, при которой
мантисса отвечает условию:
q-1
qp,
где
mA -
мантисса числа, q - основание системы
счисления, p - порядок числа.
Для
однозначности представления чисел c
плавающей точкой используется
нормализованная форма, при которой
мантисса отвечает условию:
q-1 ![]() |mА|
< 1.
Это
означает, что мантисса должна быть
правильной дробью и иметь после запятой
цифру, отличную от нуля.
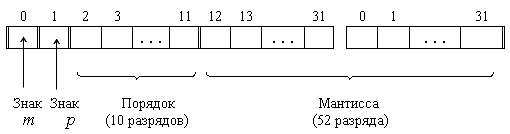
Число
в форме с плавающей точкой занимает в
памяти компьютера четыре или восемь
байт. При записи числа с плавающей точкой
выделяются разряды для хранения знака
мантиссы, знака порядка, порядка и
мантиссы. Любое вещественное число в
современных компьютерах представляется
в экспоненциальной форме с нормализованной
мантиссой. При этом мантисса является
правильной двоичной дробью, а порядок
- целым числом.
Пример. Преобразуйте
десятичное число 888,888, записанное в
естественной форме, в экспоненциальную
форму с нормализованной
мантиссой.
Решение. 888,888
= 0,888888
103
Нормализованная
мантисса mА =
0,888888, порядок p = 3.
|mА|
< 1.
Это
означает, что мантисса должна быть
правильной дробью и иметь после запятой
цифру, отличную от нуля.
Число
в форме с плавающей точкой занимает в
памяти компьютера четыре или восемь
байт. При записи числа с плавающей точкой
выделяются разряды для хранения знака
мантиссы, знака порядка, порядка и
мантиссы. Любое вещественное число в
современных компьютерах представляется
в экспоненциальной форме с нормализованной
мантиссой. При этом мантисса является
правильной двоичной дробью, а порядок
- целым числом.
Пример. Преобразуйте
десятичное число 888,888, записанное в
естественной форме, в экспоненциальную
форму с нормализованной
мантиссой.
Решение. 888,888
= 0,888888
103
Нормализованная
мантисса mА =
0,888888, порядок p = 3.
Представление чисел в форме с плавающей точкой очень удобно для решения научных и инженерных задач. Нормализованное представление чисел не только позволяет сохранить в разрядной сетке большое количество значащих цифр, но также упрощает действие над порядками и мантисами.
Для представления чисел с плавающей точкой (ЧПТ) используется полулогарифмическая форма записи числа:
N = ± mq ± p
где q- основание системы счисления, p - порядок числа, m - мантисса числа N.
Положение точки определяется значением порядка p. С изменением порядка точка перемещается (плавает) влево или вправо. Пример.
12510=12.5*101=1.25*102=0.125*103=0.0125*104=...
Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне: 1/q ≤ | m | < 1. Таким образом в нормализованных числах цифра после точки должна быть значащей.
Пример.
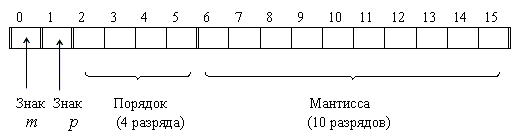
Для представления чисел в машинном слове выделяют группы разрядов для изображения мантиссы, порядка, знака числа и знака порядка: а) представление чисел в формате полуслова
б) представление чисел в формате слова
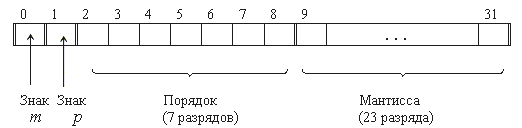
Наиболее типично представление ЧПТ в формате слова (32 разряда).Таким образом числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. При записи числа в формате слова диапазон представимых чисел будет от -1·2127 до 1·2127 (21271038), а точность определяться мантиссой, состоящей из 23 разрядов. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):