
- •Змістовий модуль III
- •1. Що таке генератор? За якими ознаками можна класифікувати генератори?
- •2. Якої найвищої стабільності (за порядком величини) можна досягти, використовуючи кварцову стабілізацію?
- •3. Чому на низьких (звукових) частотах краще застосовувати rc- автогенератори?
- •4. В чому полягає ідея створення rc- автогенератора?
- •5. Яким вимогам має задовольняти чотириполюсник зворотного зв’язку в rc- автогенераторі?
- •7. Чому форма коливань, генерованих rc-автогенераторами, звичайно відрізняється від гармонічної? Що треба робити щоб наблизитись до гармонічної форми генерованих коливань?
- •8. Навіщо в rc-автогенераторі з мостом Віна потрібне коло негативного зворотного зв’язку RззR0?
- •9. Навіщо для покращення форми генерованих коливань в rc-автогенераторі з мостом Віна послідовно з резистором r0 вмикають лампочку розжарення?
- •10. Чому навіть при повністю симетричній схемі мультивібратор не може перебувати в симетричному режимі?
- •11. Яким процесом визначається час перебування одного з транзисторів (наприклад, vt1) в закритому стані? Оцініть цей час.
- •13. Чому передній фронт імпульсів колекторної напруги має закруглену форму, тоді як задній фронт різкий?
- •14. Чим можна пояснити невеликий позитивний заряд напруги uб, який з’являється в момент відкривання транзистора? Чим визначається тривалість цього викиду?
- •15. Чи зможе мультивібратор працювати, якщо не буде виконуватись умова насичення відкритого транзистора?
- •16. Чому в мультивібраторі не вдається одержати імпульси з високою шпаруватістю?
- •17. Чому у мультивібраторах не рекомендується брати великий запас для виконання умови насичення транзистора?
- •18. Чи можна вдосконалити мультивібратор, щоб і передній і задній фронти генерованих ним імпульсів були різкими?
- •19. Чому в очікувальному мультивібраторі з емітерним зв’язком передній фронт вихідного імпульсу різкий, а не закруглений як у звичайного мультивібратора з емітерно-базовими зв’язками?
- •20. Чим визначається проміжок часу після закінчення вихідного імпульсу, коли очікувальний мультивібратор з емітерним зв’язком стане знову придатним для спрацювання від наступного пускового імпульсу?
- •21. Чому схема симетричного тригера не може перебувати в симетричному режимі?
- •22. Чи може функціонувати тригер, якщо його відкритий транзистор не перебуватиме в режимі насичення?
- •23. Чому для побудови тригера бажано застосувати кремнієві, а не германієві транзистори?
- •24. Для чого у тригері рекомендується шунтувати опір зв’язку r1 невеликою ємністю?
- •25. Чому для керування тригером краще подавати позитивний імпульс на базу закритого транзистора, а не негативний - на базу відкритого?
- •26. Поясніть, чому тригер називають елементом електронної пам’яті.
- •27. Чому тригер Шмідта називають бістабільним?
- •28. З якою метою застосовують тригери Шмідта?
- •Змістовий модуль IV
- •1. В чому полягають принципи аналогового та цифрового подання інформації?
- •2. Наведіть приклади аналогового та цифрового зображення величин. Проаналізуйте переваги та недоліки кожного.
- •3. Детально опишіть алгоритм переходу від аналогової форми подання інформації до цифрової.
- •4. Що таке дискретизація за часом? Сформулюйте теорему Котельникова.
- •5. В чому суть квантування аналогового сигналу? Що собою являють шуми квантування і чому вони виникають?
- •6. В чому полягає кодування інформації?
- •7. Що таке дворівневий код та як відбувається зображення інформації у вигляді двійкових чисел?
- •8. Проаналізуйте переваги та недоліки цифрової форми подання інформації.
- •9. Які системи числення ви знаєте? Наведіть їхню порівняльну характеристику.
- •10. Що таке цифровий ключ? Детально опишіть роботу біполярного насиченого ключа.
- •11. Як працюють цифрові ключі на мдн—транзисторах?
- •12. Що є фізичною причиною існування інерційності цифрових ключів? Які способи зменшення інерційності цифрових ключів ви знаєте?
- •13. Що таке логічні елементи?
- •14.В чому полягає суть операцій повторення та інверсії? Наведіть приклади реальних схем.
- •15. В чому полягає суть операції диз’юнкції? Наведіть приклади реальних схем.
- •16. В чому полягає суть операції кон’юнкції? Наведіть приклади реальних схем.
- •17. В чому полягає суть операції “або—не”? Наведіть приклади реальних схем.
- •18. В чому полягає суть операції “і—не”? Наведіть приклади реальних схем.
- •19. В чому полягає суть операцій рівнозначність та нерівнозначність? Наведіть приклади реальних схем.
- •20. Що таке логічні елементи з трьома вихідними станами? Для чого вони використовуються?
- •21. Що таке логічні інтегральні мікросхеми? Наведіть приклад функціонально повної системи логічних елементів.
- •22. Що таке суматор? Опишіть принцип дії суматора використовуючи поняття про доповняльний код.
- •23. Що таке дешифратор? Як він працює? Де використовується?
- •24. Що таке селектор? Як він працює? Де використовується?
- •25. Що таке мультиплексор? Опишіть принцип його дії.
- •26. Формувачі імпульсів: класифікація та принципи дії.
- •27. Запам’ятовуючі пристрої. Наведіть загальні характеристики запам’ятовуючих пристроїв та їхню класифікацію.
- •28. Що таке тригери? Де вони використовуються? Наведіть приклади.
- •29. Що таке регістр? Які типи регістрів ви знаєте? Наведіть приклади.
- •30. Що таке лічильник? Де вони застосовуються. Наведіть приклади.
- •31. Що таке коефіцієнт перерахунку лічильника? Як ним можна керувати? Наведіть приклади.
- •32. Що таке оперативні запам’ятовуючі пристрої? Які озп ви знаєте? Дайте загальну характеристику озп.
- •33. Детально опишіть принцип роботи статичного озп.
- •34. Детально опишіть принцип роботи динамічного озп.
- •35. Проаналізуйте переваги та недоліки статичних та динамічних озп.
- •36. Що таке постійні запам’ятовуючі пристрої. Які пзп ви знаєте?
- •37. Як побудовані та за яким принципом працюють масочні пзп?
- •38. В чому відмінність пзп та програмованих пзп? Наведіть приклади програмованих пзп.
- •39. За яким принципом працюють перепрограмовані пзп?
- •40. Що таке флеш—пам’ять? Як вона побудована? Порівняйте флеш—пам’ять типу nor та nand.
15. В чому полягає суть операції диз’юнкції? Наведіть приклади реальних схем.
Диз’юнкція (логічне додавання, операція “АБО”): y = x1 v x2;
Логічна одиниця на виході диз’юнктора виникає тоді, коли хоча б один з аргументів, або обидва є логічними одиницями. Умовне зображення диз’юнктора наведено на рис.
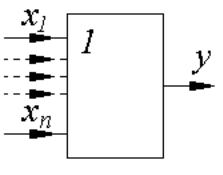
Він може мати кілька входів та лише один вихід. Електрична схема, що реалізує операцію “АБО”, складається з кількох паралельно увімкнених ключів (рис. 6.26, а), кожен з яких замикається, коли відповідний вхідний сигнал дорівнює “1”.
Конкретна схема, здатна реалізувати операцію “АБО”, складається з
паралельно увімкнених транзисторних ключів, на бази яких подаються
відповідні вхідні сигнали хі (рис. 6.26, б). На спільному емітерному опорі
RE сигнал високого рівня з’являється тоді, коли хоча б один з
транзисторів відкривається своїм вхідним сигналом.
Оскільки усі транзистори зв’язані через спільний емітерний опір RE, то подібні схеми називають схемами з емітерно-зв’язаною логікою(ЕЗЛ).

Рис.6.26
16. В чому полягає суть операції кон’юнкції? Наведіть приклади реальних схем.
Кон’юнкція (логічне множення, операція “І”): y = x1 Ʌ x2
Операція кон’юнкція має зміст множення. Дійсно, лише коли обидва
аргументи х1 та х2 одночасно дорівнюють “1”функція у набуває значення “1”.
В усіх інших випадках у=“0”. Кон’юнктор, як і диз’юнктор, може мати декілька входів і лише один вихід.

Реалізувати операцію кон’юнкції можна за допомогою групи ключів, що працюють на розмикання, коли вхідний сигнал є логічною одиницею
(рис. 6.28, а, б).
Лише тоді, коли усі ключі будуть розімкнені, сигнал на виході схеми буде відповідати логічній одиниці (у=“1”).
Якщо ж хоча б один з ключів лишається замкненим,
вихідний сигнал дорівнюватиме логічному нулю. Як правило, транзистори у таких схемах об’єднують, створюючи так званий багатоемітерний транзистор (рис. 6.29), що має одну базу, один колектор та декілька емітерів. Для зменшення впливу навантаження на режим роботи транзистора VT1 і збільшення потужності вихідного сигналу використовують ще й емітерний повторювач на транзисторі VT2.
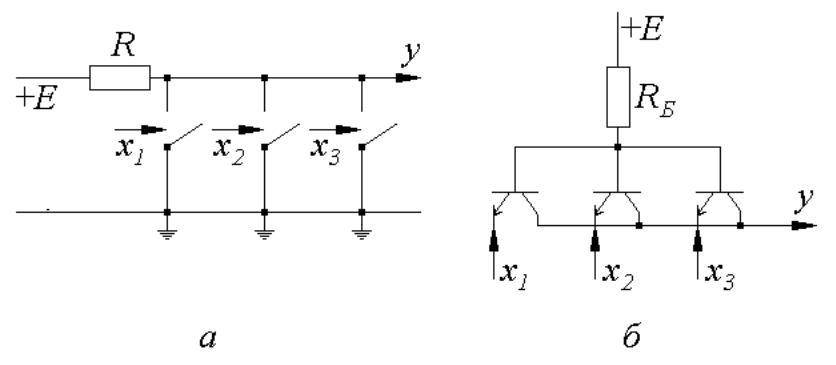
Рис.6.28

Рис.6.29
17. В чому полягає суть операції “або—не”? Наведіть приклади реальних схем.
Операція “АБО-НЕ” є операцією диз’юнкції з наступним запереченням:
y
=
 .
.
Лише тоді, коли усі вхідні аргументи є нулями, на виході встановлюється сигнал високого рівня.Здійснити таку операцію легко,увімкнувши послідовно диз’юнктор та інвертор (рис. 6.30). Проте, насправді є ще простіший ш лях: у схемі диз’юнктора, наведеній на рис. 6.26 опір R слід увімкнути не в коло емітера, а в коло колектора, як це показано на рис. 6.31. Такий узагальнений диз’юнктор-інвертор має умовне позначення, наведене на рис. 6.32.
 Рис.6.30
Рис.6.30
 Рис.6.32
Рис.6.32
 Рис.6.31
Рис.6.31
18. В чому полягає суть операції “і—не”? Наведіть приклади реальних схем.
Аналогічно можна побудувати пристрій, який реалізує операцію “І-НЕ”
(
y =
 ). Тут високий рівень сигналу на виході
має місце тоді, коли хоча б один з вхідних
сигналів хі дорівнює нулю. Таку
схемі легко створити, увімкнувши в
кон’юнкторі інвертор замість емітерного
повторювача (рис. 6.33). Логічний елемент
“І-НЕ” має умовне позначення,зображене
на рис. 6.34.
). Тут високий рівень сигналу на виході
має місце тоді, коли хоча б один з вхідних
сигналів хі дорівнює нулю. Таку
схемі легко створити, увімкнувши в
кон’юнкторі інвертор замість емітерного
повторювача (рис. 6.33). Логічний елемент
“І-НЕ” має умовне позначення,зображене
на рис. 6.34.
 Рис.6.33
Рис.6.33
 Рис.6.34
Рис.6.34
Особливістю логічних елементів “АБО-НЕ” та “І-НЕ” є їхня універсальність. Адже з них можна побудувати пристрої, які здатні здійснювати усі попередньо перераховані логічні операції, просто з’єднуючи їх у тій чи іншій послідовності.
