3. Детально опишіть алгоритм переходу від аналогової форми подання інформації до цифрової.

Щоб перейти від графічної (аналогової) форми подання процесу A(t) до табличної (цифрової) слід виконати такі операції:

• розділити весь інтервал часу t на ряд рівних проміжків (теорема Котельникова , де – максимальна частота, якою обмежений спектр сигналу (або максимальна потрібна частота);

• у вибрані моменти часу виміряти значення величини A(t) (дискретизація у часі);

• проведені виміри слід зробити з необхідною точністю, тобто слід округлити істинні значення величини A(t) до певного дискретного значення (квантування);

• одержані дискретні значення величини A(t) слід зобразити у вигляді символічних знаків (кодування).

Процес зображення чисел умовними символами (кодом) називається кодуванням.

4. Що таке дискретизація за часом? Сформулюйте теорему Котельникова.

Дискретизація у часі (перший етап перетворення аналогової інформації у цифрову) – етап,коли виміри значень інформативної величини здійснюються через визначені інтервали часу ∆t. Значення інтервалу ∆t не повинне бути надто великим, оскільки відбуватимуться втрати дрібних деталей у поведінці носія інформації між вимірами. Проте, при надто частих вимірюваннях, коли значення інтервалу ∆t надто мале, інформація може виявитися зайвою. Очевидно, що для повільно-змінної функції вимірювання можна здійснювати порівняно рідко, тоді як для швидкозмінної функції – значно частіше.

Теорема Котельнікова визначає кількісне значеня необхідного інтервалу ∆t між вимірами.

(1)

де 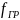- найвища частота у спектрі функції.

Таким чином, замість того, щоб передавати усю неперервну функцію A(t), можна обмежитися передачею послідовності коротких імпульсів, амплітуди яких пропорційні до миттєвих значень функції A(t) у моменти вимірювань.

При виконанні умови (1) у точці прийому неперервна функція A(t) може бути відновлена у вигляді огинаючої цих імпульсів:

5. В чому суть квантування аналогового сигналу? Що собою являють шуми квантування і чому вони виникають?

Квантування сигналу – розбиття усієї шкали значень функції A(t) на ряд дискретних рівнів ,та «привёязування» істинного значення сигналу до найближчого з них.

Шуми квантування - неточності та спотворення, що виникають при заміні істинних значень сигналу на дискретні ( є еквівалентом до появи у передавальному тракті шумів). Шуми квантування будуть тим меншими, чим меншим є крок квантування, тобто інтервал між сусідніми рівнями квантування. Природною межею кроку квантування є рівень власних шумів, які завжди присутні у аналоговому сигналі і обмежують точність вимірювання його параметрів.

6. В чому полягає кодування інформації?

Останнім етапом перетворення аналогової інформації на цифрову є кодування сигналу, тобто подання числа, отриманого на етапі квантування сигналу, у вигляді умовного кодового символу. При передачі цифрової інформації у вигляді електричних сигналів такими символами можуть бути групи імпульсів струму чи напруги. Наприклад, у коді Морзе використовують імпульси двох типів – короткі (крапки) і довгі (тире), загальна кількість яких у різних літерах та цифрах може бути різною.

Більш зручним для передачі інформації у вигляді електричних сигналів є код Бодо, у якому кожна кодове “слово” складається з певної кількості однакових прямокутних імпульсів. Одне таке “слово” відрізняється від іншого тим, що певні імпульси у “слові” пропущені. Якщо кодове “слово” складається з 5 імпульсів, то з них можна побудувати 32 неповторних комбінації, а якщо з 6 імпульсів – 64 комбінації. Такої кількості комбінацій достатньо, щоб закодувати усю абетку, десять арабських цифр та ряд допоміжних знаків.

Таке 6-ти значне (6-ти розрядне) кодове слово легко співвіднести з числом у двійковій формі запису.

Нехай тепер присутність імпульсу в n-тому розряді кодового слова Бодо відповідає логічній одиниці в n-тому розряді двійкового числа, а пропущений імпульс – відповідає логічному нулю.