
- •Ответы на билеты
- •Предсказание. Определение. Классификации.
- •2.Задачи и методы социально-экономического прогнозирования.
- •3. Число. Шкала. Зависимость применимости методов прогнозирования от шкалы.
- •4. Анализ динамического ряда. Виды трендов.
- •5. Сглаживание динамического ряда. Сравнительный анализ.
- •6. Метод скользящей средней при нечетной базе сглаживания.
- •Сглаживание по нечётной базе
- •7. Метод скользящей средней при четной базе сглаживания.
- •8. Достоинства и недостатки метода скользящей средней.
- •Достоинства и недостатки метода
- •9. Метод экспоненциального сглаживания.
- •11. Зависимость результата экспоненциального сглаживания от всего ряда данных. Достоинства и недостатки метода экспоненциального сглаживания.
- •12. Прогнозирование на основе сплайн-функций.
- •13. Прогнозирование на основе аналитического тренда. Критерии соответствия тренда исходным данным. Метод наименьших квадратов.
- •Метод наименьших квадратов
- •Система уравнений для линейного тренда
- •Система уравнений для экспоненциального тренда
- •14. Способы определения типа тренда. Тест на линейную функцию.
- •Определение тренда на основе сглаживания ряда
- •15. Определение параметров линейного тренда. Смысл параметров линейного тренда. Прогнозирование на основе линейного тренда.
- •16. Определение параметров экспоненциального тренда. Смысл параметров экспоненциального тренда. Прогнозирование на основе экспоненциального тренда.
- •17. Понятие сезонности. Природа, виды сезонных колебаний.
- •18. Процедура выявления аддитивной сезонной составляющей ряда данных.
- •19. Процедура выявления мультипликативной сезонной составляющей ряда данных.
- •20. Построение прогноза с учетом сезонных колебаний.
- •21. Экстраполяция и интерполяция. Критерии точности прогноза.
- •Критерии для оценки точности прогноза
- •22. Регрессия. Отбор факторов для регрессии.
- •Отбор факторов для регрессии
- •23. Производственная функция и ее смысл. Виды производственных функций.
- •24. Смысл и расчёт параметров производственной функции Кобба-Дугласа. Прогнозирование на основе производственной функции Кобба-Дугласа.
- •25. Факторный анализ. Порядок проведения. Направления использования.
- •26. Сетевое планирование. Построение плана.
- •27. Сетевое планирование. Оптимизация плана.
- •28. Сценарное прогнозирование.
- •29. Постановка задачи линейного планирования. Экономические интерпретации задачи.
- •30. Определение устойчивости решения задачи линейного планирования при изменении целевой функции. Экономические интерпретации задачи. Графическая интерпретация решения.
- •31. Определение устойчивости решения задачи линейного планирования при изменении правых частей ограничений. Экономические интерпретации задачи. Графическая интерпретация решения.
- •32. Экспертные оценки. Сфера применения и порядок проведения.
- •33. Экспертные оценки. Варианты построения коллективной экспертной оценки.
- •34. Экспертные оценки с учётом компетентности экспертов.
- •Выбор экспертов
- •Организация взаимодействия экспертов
- •35. Имитационное моделирование. Сфера применения и порядок проведения.
- •36. Стандартизированная случайная величина. Датчик случайных чисел. Моделирование случайной величины с произвольной функцией распределения.
- •38. Система массового обслуживания. Схема. Основные характеристики.
- •39. Система массового обслуживания. Поток требований.
- •40. Система массового обслуживания. Механизм обслуживания.
- •41. Система массового обслуживания. Дисциплина очереди.
- •42. Самореализующиеся прогнозы.
36. Стандартизированная случайная величина. Датчик случайных чисел. Моделирование случайной величины с произвольной функцией распределения.
Нормальная
случайная величина:![]() :
: 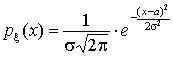 Стандартная
нормальная случайная величина:
Стандартная
нормальная случайная величина: ![]()
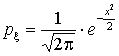 Любая
нормальная случайная величина:
Любая
нормальная случайная величина: ![]() ,
где
,
где ![]() Таким
образом достаточно получить датчик
стандартной нормальной случайной
величины.
Таким
образом достаточно получить датчик
стандартной нормальной случайной
величины.
Методы:
Метод суммирования
/*
ЦПТ: Для независимых случайных
величин ![]() произвольным
распределением
произвольным
распределением
![]() .*/
.*/
Пусть ![]() ясно,
что
ясно,
что ![]() ,
, ![]() .
Тогда
.
Тогда 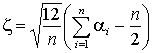 Если
взять
Если
взять ![]() ,
то получим
,
то получим
![]()
Существуют
более точные формулы, типа ![]() .
В частности, для
:
.
В частности, для
:
![]()
Метод обратной функции
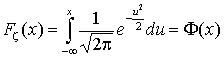 -
интеграл вероятностей или функция
Лапласа.
Свойство:
-
интеграл вероятностей или функция
Лапласа.
Свойство: 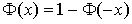 Метод
обратной функции:
Метод
обратной функции: 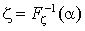
Очевидно,
что ![]()
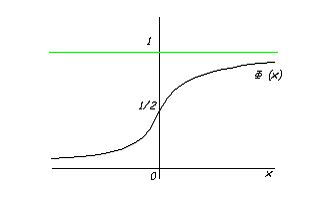

 Т.
о.
Т.
о. ![]() заменяют
аппроксимациями.
заменяют
аппроксимациями.
Для моделирования случайных величин, имеющих произвольную функцию распределения, необходимо использовать специальные методы. Например, Метод Неймана.
Метод Неймана является методом, позволяющим получить значения СВ в соответствии с заданным законом распределения. Этот метод является достаточно универсальным он применим для моделирования всех СВ, значения которых не выходят за пределы ограниченного интервала (a,b), а также для СВ, законы распределения которых можно аппроксимировать усеченными.
Метод
Неймана состоит в следующем:
С помощью
датчика случайных чисел получают пару
псевдослучайных чисел, распределенных
равномерно на (0,1).x1 и x2.
Затем получают
два числа , равномерно распределенных
соответственно на интервалах (a,b) и
(o,w), то есть
![]() ,
где
рис
3.5.
,
где
рис
3.5.
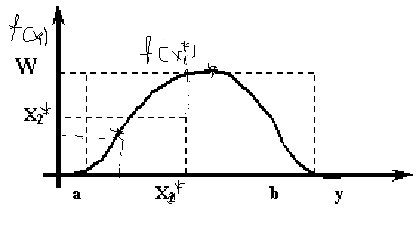
Из точек с координатами выбирают те, которые попали “под колокол” функции fh (y), то есть те точки, для которых. Если выполнено условие 3., то искомое значение y полагают равным.
37. Система массового обслуживания. Классификация.
Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и оборудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания.
В теории систем массового обслуживания (в дальнейшем просто -CMО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.
Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, мастера-ремонтники, билетные кассиры, погрузочно-разгрузочные точки на базах и складах.
Совокупность однотипных обслуживающих устройств называется обслуживающими устройствами. Такими системами могут быть телефонные станции, аэродромы, билетные кассы, ремонтные мастерские, склады и базы снабженческо-сбытовых организаций и т.д.
В теории СМО рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. носит случайный характер. В силу этих причин одним из основных методов математического описания СМО является аппарат теории случайных процессов .
Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств.
Классификация СМО и их основные элементы
СМО классифицируются на разные группы в зависимости от состава и от времени пребывания в очереди до начала обслуживания, и от дисциплины обслуживания требований.
По составу СМО бывают одноканальные (с одним обслуживающим устройством) и многоканальными (с большим числом обслуживающих устройств). Многоканальные системы могут состоять из обслуживающих устройств как одинаковой, так и разной производительности.
По времени пребывания требований в очереди до начала обслуживания системы делятся на три группы:
1) с неограниченным временем ожидания (с ожиданием),
2) с отказами;
3) смешанного типа.
В СМО с неограниченным временем ожидания очередное требование, застав все устройства занятыми, становится в очередь и ожидает обслуживания до тех пор, пока одно из устройств не освободится.
В системах с отказами поступившее требование, застав все устройства занятыми, покидает систему. Классическим примером системы с отказами может служить работа автоматической телефонной станции.
В системах смешанного типа поступившее требование, застав все (устройства занятыми, становятся в очередь и ожидают обслуживания в течение ограниченного времени. Не дождавшись обслуживания в установленное время, требование покидает систему.
В системах с определенной дисциплиной обслуживания поступившее требование, застав все устройства занятыми, в зависимости от своего приоритета, либо обслуживается вне очереди, либо становится в очередь.
