
- •Ответы на билеты
- •Предсказание. Определение. Классификации.
- •2.Задачи и методы социально-экономического прогнозирования.
- •3. Число. Шкала. Зависимость применимости методов прогнозирования от шкалы.
- •4. Анализ динамического ряда. Виды трендов.
- •5. Сглаживание динамического ряда. Сравнительный анализ.
- •6. Метод скользящей средней при нечетной базе сглаживания.
- •Сглаживание по нечётной базе
- •7. Метод скользящей средней при четной базе сглаживания.
- •8. Достоинства и недостатки метода скользящей средней.
- •Достоинства и недостатки метода
- •9. Метод экспоненциального сглаживания.
- •11. Зависимость результата экспоненциального сглаживания от всего ряда данных. Достоинства и недостатки метода экспоненциального сглаживания.
- •12. Прогнозирование на основе сплайн-функций.
- •13. Прогнозирование на основе аналитического тренда. Критерии соответствия тренда исходным данным. Метод наименьших квадратов.
- •Метод наименьших квадратов
- •Система уравнений для линейного тренда
- •Система уравнений для экспоненциального тренда
- •14. Способы определения типа тренда. Тест на линейную функцию.
- •Определение тренда на основе сглаживания ряда
- •15. Определение параметров линейного тренда. Смысл параметров линейного тренда. Прогнозирование на основе линейного тренда.
- •16. Определение параметров экспоненциального тренда. Смысл параметров экспоненциального тренда. Прогнозирование на основе экспоненциального тренда.
- •17. Понятие сезонности. Природа, виды сезонных колебаний.
- •18. Процедура выявления аддитивной сезонной составляющей ряда данных.
- •19. Процедура выявления мультипликативной сезонной составляющей ряда данных.
- •20. Построение прогноза с учетом сезонных колебаний.
- •21. Экстраполяция и интерполяция. Критерии точности прогноза.
- •Критерии для оценки точности прогноза
- •22. Регрессия. Отбор факторов для регрессии.
- •Отбор факторов для регрессии
- •23. Производственная функция и ее смысл. Виды производственных функций.
- •24. Смысл и расчёт параметров производственной функции Кобба-Дугласа. Прогнозирование на основе производственной функции Кобба-Дугласа.
- •25. Факторный анализ. Порядок проведения. Направления использования.
- •26. Сетевое планирование. Построение плана.
- •27. Сетевое планирование. Оптимизация плана.
- •28. Сценарное прогнозирование.
- •29. Постановка задачи линейного планирования. Экономические интерпретации задачи.
- •30. Определение устойчивости решения задачи линейного планирования при изменении целевой функции. Экономические интерпретации задачи. Графическая интерпретация решения.
- •31. Определение устойчивости решения задачи линейного планирования при изменении правых частей ограничений. Экономические интерпретации задачи. Графическая интерпретация решения.
- •32. Экспертные оценки. Сфера применения и порядок проведения.
- •33. Экспертные оценки. Варианты построения коллективной экспертной оценки.
- •34. Экспертные оценки с учётом компетентности экспертов.
- •Выбор экспертов
- •Организация взаимодействия экспертов
- •35. Имитационное моделирование. Сфера применения и порядок проведения.
- •36. Стандартизированная случайная величина. Датчик случайных чисел. Моделирование случайной величины с произвольной функцией распределения.
- •38. Система массового обслуживания. Схема. Основные характеристики.
- •39. Система массового обслуживания. Поток требований.
- •40. Система массового обслуживания. Механизм обслуживания.
- •41. Система массового обслуживания. Дисциплина очереди.
- •42. Самореализующиеся прогнозы.
24. Смысл и расчёт параметров производственной функции Кобба-Дугласа. Прогнозирование на основе производственной функции Кобба-Дугласа.
Впервые
производственную функцию степенного
вида предложили использовать в виде:
![]() ,
где:
,
где:
Если
в качестве ресурсов выступают только
два фактора – капитал К и труд L, говорят
о функции Кобба-Дугласа:
![]() .
Данная функция отличается простотой
расчёта основных характеристик и
интерпретации параметров.
.
Данная функция отличается простотой
расчёта основных характеристик и
интерпретации параметров.
Величина отдачи на масштаб определяется суммой степеней. Если
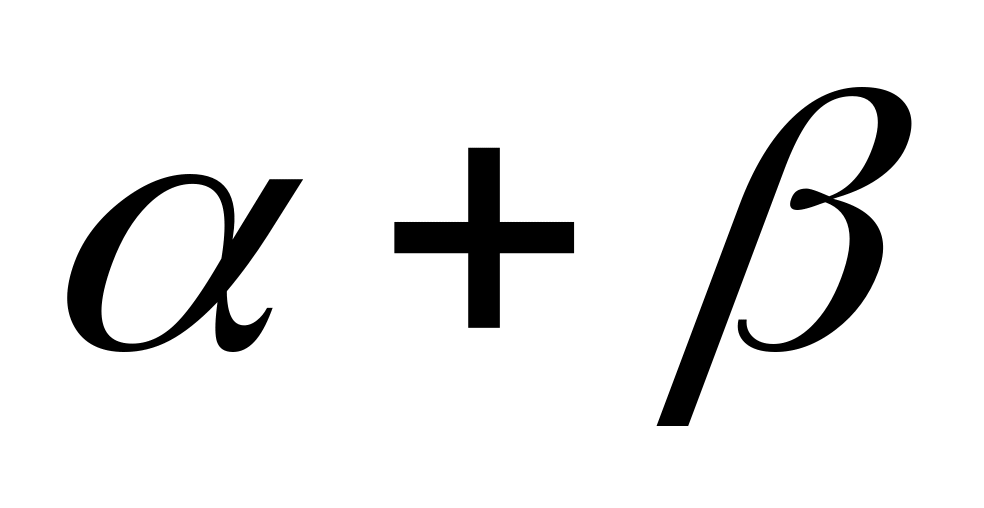 >=<1
имеет место растущая/постоянная/падающая
отдача на масштаб.
>=<1
имеет место растущая/постоянная/падающая
отдача на масштаб.Изокванта
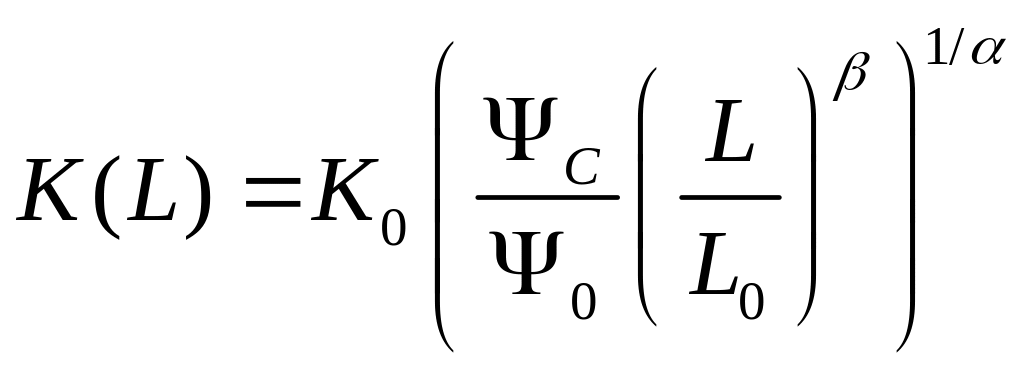 асимптотически
приближается к осям. Предельная норма
замещения
асимптотически
приближается к осям. Предельная норма
замещения
 .
Эластичность замещения ресурсов
.
Эластичность замещения ресурсов
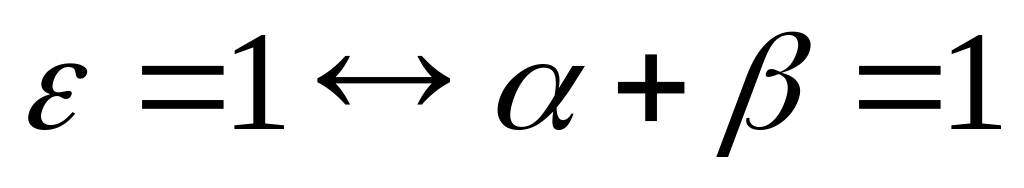
Эластичность выпуска по ресурсам

К недостаткам функции можно отнести предположения о полной взаимозаменяемости ресурсов, постоянстве структуры капитала с ростом выпуска, постоянстве эффективности производства.
Субстиционная производственная функция имеет в общем следующее выражение:
![]()
где:
K – число производственного капитала
L – число производственных трудовых часов или, другими словами, число производственных единиц гуманного капитала.
Каждое увеличение количественного параметра имущественного капитала означает смещение кривой вверх и одновременного увеличения предельной производительности труда при заданном количестве рабочей силы, т.е. на основе вытекающего непосредственно из описанного вывода означает и более высокую величину выпуска при увеличении производственного фактора «труд»: кривая OK1 .
С увеличением количественного параметра имущественного капитала увеличивается и средняя производительности труда, которая является частным от деления величины выпуска на величину затраченного труда. Однако при этом уменьшается коэффициент труда, определяющий среднее количество затраченного труда на каждую единицу выпуска и являющийся таким образом обратной величиной средней производительности труда.
Кинетическая
функция
![]()
(где g - норма технического прогресса за единицу времени) получена умножением функции Кобба-Дугласа на eg, что снимает данную проблему и делает
функцию Кобба-Дугласа экономически интересной.
Эластичность выпуска продукции по капиталу и труду равна соответственно a и b, так как
![]() ,
,
и аналогичным образом легко показать, что (dy/dL)/(y/L) равно b.
Следовательно, увеличение затрат капитала на 1% приведет к росту выпуска продукции на a процентов, а увеличение затрат труда на 1% приведет к росту выпуска на b процентов. Можно предположить, что обе величины a и b находятся между нулем и единицей. Они должны быть положительными, так как увеличение затрат производственных факторов должно вызывать рост выпуска. В то же время, вероятно, они будут меньше единицы, так как разумно предположить, что уменьшение эффекта от масштаба производства приводит к более медленному росту выпуска продукции, чем затрат производственных факторов, если другие факторыостаются постоянными.
Если a и b в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то y растет в большей пропорции).
Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства (y увеличивается в той же пропорции, что и К и L). Если их сумма меньше, чем единица, то имеет место убывающий эффект от масштаба производства (y увеличивается в меньшей пропорции, чем К и L).
В соответствии с допущением о конкурентности рынков факторов производства и b имеют дальнейшую интерпретацию как прогнозируемые доли дохода, полученного соответственно за счет капитала и труда. Если рынок труда имеет конкурентный характер, то ставка заработной платы (w) будет равна предельному продукту труда (dy/dL):
![]() .
.
Следовательно, общая сумма заработной платы (wL) будет равна by, а доля труда в общем выпуске продукции (wL/Y) составит постоянную величину b. Аналогичным образом норма прибыли выражается через dy/dK:
![]() ,
,
и, следовательно, общая прибыль (rК) будет равна ay, а доля прибыли будет постоянной величиной a.
Существует ряд проблем по применению такой функции, особенно в тех случаях, когда она используется для экономики в целом. В частности, даже в тех случаях, когда между выпуском продукции, производственным оборудованием и трудом в производственном процессе существует технологическая зависимость, то совершенно необязательно, что подобная зависимость существует тогда, когда указанные факторы комбинируются в масштабах экономики в целом. Во-вторых, даже если такая зависимость для экономики в целом существует, то нет никаких оснований считать, что она будет иметь простую форму.
При построении производственной функции Кобба–Дугласа параметры A, a, b можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов (МНК):
1) Производственную функцию Кобба–Дугласа приводят к линейному виду путем логарифмирования
![]()
2)
При применении МНК цель заключается
в минимизации суммы квадратичных
отклонений (SSD) между наблюдаемыми
величинами ln(yi),
(i=1.N; N –количество наблюдений) и
соответствующими оценками
![]()
![]()
3) Введем векторы
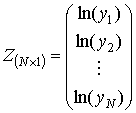 ;
;
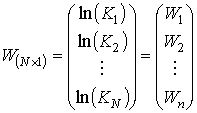 ;
;
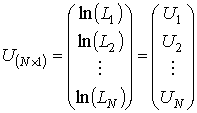 ;
;
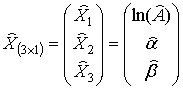
и
матрицу
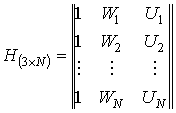
Тогда критерий можно записать в виде
![]() .
.
Дифференцируя SSD по вектору Х и приравнивая производную к нулю систему уравнений МНК
![]()
или
![]() .
.
4) Для оценки критерия значимости выборочных коэффициентов регрессии оценивают дисперсию выборочных коэффициентов
![]() ,
,
где
cii
– элементы главной диагонали матрицы
![]() .
.
s2 – дисперсия погрешности измерений.
Оценка s2 определяется по формуле
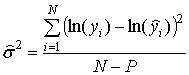
Рассчитывается значение t – параметра
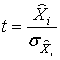
Если полученное значение t больше, чем табличное ta при (N-3-1) степеней свободы, тогда Xi существенно отлично от нуля при уровне a.
Доверительные
границы для
![]() определяются
по формуле
определяются
по формуле
![]()
Тогда вероятность того, что величина Xi действительно находится в этих пределах, составит 1–a.
5) Для оценки адекватности регрессивной модели наблюдаемым величинам объема выпуска y рассчитывается коэффициент множественной детерминации:
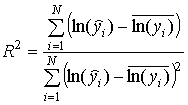 ,
,
где
![]() .
.
При малом объеме выборки используется скорректированный коэффициент множественной детерминации
![]()
Чем
меньше отличается
![]() от единицы, тем более обосновано решение
о том, что выборочные коэффициенты
регрессии могут быть полезны для изучения
производственного процесса.
от единицы, тем более обосновано решение
о том, что выборочные коэффициенты
регрессии могут быть полезны для изучения
производственного процесса.
