Оценка риска в финансовом менеджменте (Количественный анализ)

Дисперсия:

Среднеквадратическое отклонение:

Коэффициент вариации:

где D — дисперсия;

Di — конкретное значение возможных вариантов ожидаемого дохода по рассматриваемой финансовой операции;

— среднее ожидаемое значение дохода по рассматривае­мой финансовой операции;

Pi — возможная частота (вероятность) получения отдельных вариантов ожидаемого дохода по финансовой операции;

n — число наблюдений,

 — среднеквадратическое (стандартное) отклонение;

СV— коэффициент вариации.

 

Измерение доходности и риска финансовых активов

1. Доходность актива (d):

d = D / I. (3.1)

где D - до­хода, генерируемый финансовым активом

I - величина ин­вестиции в этот актив:

2. Текущая ожидаемая доходность (регулярные выплаты владельцу актива, в приложении к акциям она называется также дивидендной) - :

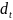3. Капитализированная ожидаемая доходность (рост стоимости самого актива) - :

Общая доходность такого финансового актива:

(3.2)

где d – доходность финансового актива;

Р₀ – цена приобретения финансового актива (в начале рассматриваемого периода);

Р₁ – цена финансового актива в конце периода (ожидаемая величина);

D₁ – регулярные выплаты в предстоящем периоде (ожидаемая величина);

D₁ + (P₁ – Р₀) – общий доход в предстоящем периоде

Оценка риска финансовых активов

1) Общей мерой риска, ассоциируемого с данным активом является размах вариации ожидаемой доходности:

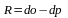(3.9)

2) Оценка рисков инвестирования в отдельные ценные бумаги:

 = ρ(и /р) (3.10)

где  — бета-коэффициент;

ρ— коэффициент корреляции между уровнем доходности по инди­видуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом;

и — среднеквадратическое отклонение доход­ности по индивидуальному виду ценных бумаг (или по их портфелю в целом);

р — среднеквадратическое отклонение доходности по фондовому рынку в целом.

3) Упрощенная формула для расчета премии за риск:

(3.11)

где - максимальная (минимальная) доходность финансового актива;

- максимальная (минимальная) среднерыночная доходность.

 = 1 — средний уровень;  > 1 — высокий уровень;

 < 1 — низкий уровень.

Модель оценки капитальных финансовых активов (capm)

1) Премия за риск вложений в рыночные (безрисковые) активы:

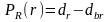(3.12)

где – премии за риск вложений в рыночные активы;

d_r – средняя рыночная доходность;

d_br – безрисковая доходность.

2) Ожидаемая премия за риск вложений в данную ценную бумагу:

и (3.13)

где – премия за риск вложений в конкретный финансовый актив;

d_а – ожидаемая доходность финансового актива,

d_r – средняя рыночная доходность;

d_br – безрисковая доходность;

 – бета-коэффициент.

3) Доходность финансового актива по модели сарм:

d_а = d_br +  (d_r – d_br) = (3.13)

В соответствии с данной моделью ожидаемая доходность акций фирмы является функцией трех взаимосвязанных параметров:

- среднерыночной доходности,

- безрисковой доходности

- присущего данной фирме β-коэффициента.

Чем выше риск, ассоциированный с данной фирмой, по сравнению со среднерыночным, тем больше премия, получаемая от инвестирования в ее ценные бумаги.

Источники финансирования предприятия по Погостинской

Источники финансирования предприятия по Ковалеву

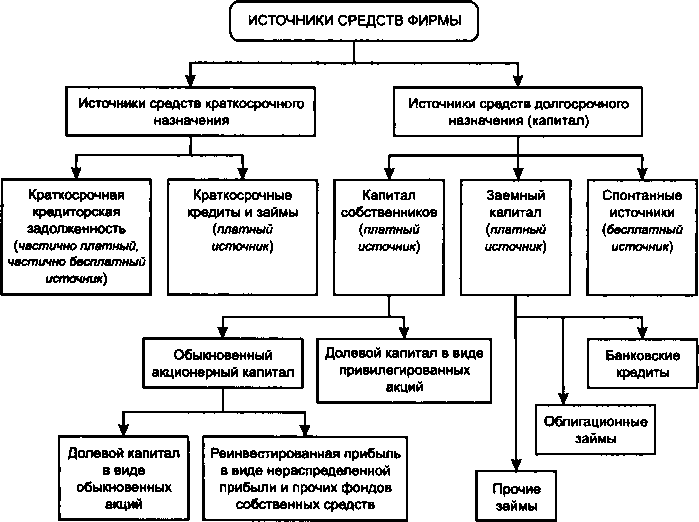
Базовые элементы стоимости заемного капитала

Стоимость финансового кредита

Банковского кредита

Финансового лизинга

Стоимость капитала привлекаемого за счет эмиссии облигаций

Стоимость товарного (коммерческого) кредита

В форме краткосрочной отсрочки платежа

В форме отсрочки платежа, оформленной векселем

Стоимость внутренней кредиторской

задолженности

Стоимость заемного капитала, привлекаемого за счет эмиссии облигаций:

Погостинская:

Ц_о = З_рд (1 – r_п),

где Ц_о – цена источника «облигационный заем»;

З_рд – относительные затраты на размещение и выплаты купонного дохода по облигации («затратность»);

r_п - ставка налога на прибыль.