21. Класичний метод аналізу перехідних процесів в rc і rl – колах.

Класичний метод розрахунку перехідних процесів заснований на складанні і наступному рішенні (інтегруванні) диференціальних рівнянь, складених за законами Кірхгофа і пов'язують шукані струми і напруги післякомутаційного ланцюга і задані впливаючі функції (джерела електричної енергії). Перетворюючи систему рівнянь, можна вивести підсумкове диференціальне рівняння відносно будь-небудь однієї змінної величини x (t):

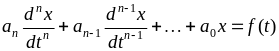. (4.2)

Тут n - порядок диференціального рівняння, він же - порядок ланцюга, коефіцієнти a_k> 0 і визначаються параметрами пасивних елементів R, L, C ланцюга, а права частина є функцією задаючих впливів.

Відповідно до класичної теорією диференціальних рівнянь повне рішення неоднорідного диференціального рівняння перебуває у вигляді суми часткового розв'язку неоднорідного диференціального рівняння і спільного рішення однорідного диференціального рівняння:

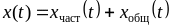. (1)

Приватне рішення повністю визначається видом правої частини f(t) диференціального рівняння. У електротехнічних завданнях права частина залежить від впливають джерел електричної енергії, тому вид обумовлюється (принуждается) джерелами електричної енергії і називається змушеною складовою .

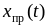Загальне рішення 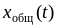однорідного диференціального рівняння залежить від коренів характеристичного рівняння, які визначаються коефіцієнтами диференціального рівняння, і не залежить від правої частини. У прикладних задачах електротехніки не залежить (вільно) від впливаючих джерел і з цієї причини називається вільною складовою і повністю визначається параметрами пасивних елементів ланцюга, а фізично процесом перерозподілу запасів енергії електричного і магнітного полів в реактивних елементах ланцюга.

Таким чином, будь-шукана величина в перехідному режимі:

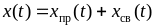. (2)

Вільну складову перехідного процесу шукають у вигляді

, (3)

де n - порядок кола, що співпадає з порядком диференціального рівняння;

p_k - корені характеристичного рівняння (власні числа ланцюга);

A_k - постійні інтегрування.

Власні числа лінійних кіл або дійсні негативні, або комплексні з негативними дійсними частинами (тобто знаходяться в лівій півплощині комплексних чисел). Тому носить перехідний (асимптотично затухаючий до нуля) характер.

Перехідні процеси в RL – колі

Якщо коло, що складається із послідовно з’єднаних опорів і індуктивностей, підключається до джерела зовнішньої напруги в момент часу t=0, тоді для t>0 справедливо рівняння:

що має рішення для струму в колі

де р- корінь характеристичного рівняння R+L_p = 0, p=-R/L; A – постійна інтегруваня, i_пр(t) визначається видом функції e(t).

Рис. 18.2

Перехідні процеси в rс – колі

Нестаціонарні явища, що виникають при заряді і розряді ємності, представляють великий практичний інтерес.

Припустимо, що RС – коло (рис. 19.1) в момент t=0 підключається до джерела зовнішньої напруги e(t). На основі другого закону Кірхгофа для t>0 рівняння кола має вигляд e(t)=Ri(t)+U_c. Оскільки

Характеристичне рівняння RC_p+1=0, звідки p=-1/RC і стала часу

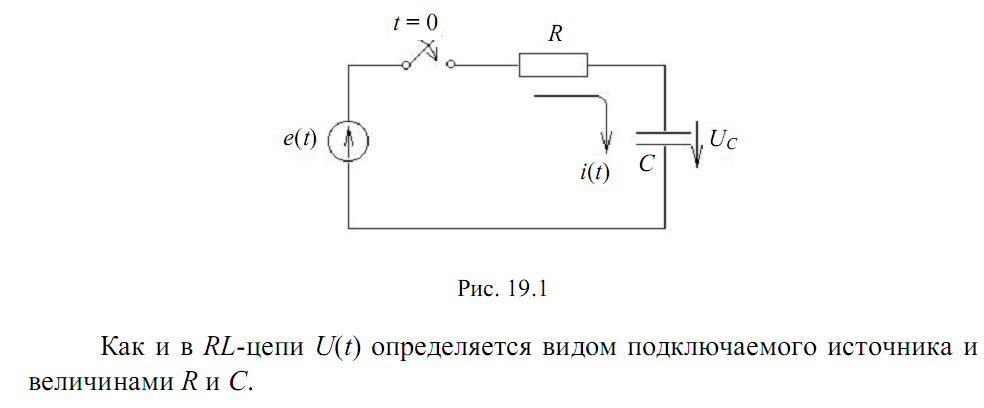
Рис. 19.1

Як і в RL – колі U(t) визначається видом підключаємого джерела і величинами R і C.