- •10. Коэф.Вязкости метод Оствальда.
- •11.Условия применимости закона Пуазейля. Ф. Пуазейля.
- •14. Закон Гука. Модуль Юнга.
- •15. Закон Ома для переменных тока и напряжения.Зависимость от частоты.
- •16. Импеданс в электрических схемах…
- •18. Понятие о мультиполе.
- •32. Понятие об аналоговых, дискретных и комбинированных регистрирующих устройствах.
- •34. Частотная (амплитудно-частотная) характеристика усилителей...
- •40. Энергетические характеристики световых потоков, поток светового волновая оптика…
- •46. Излучение Солнца. Спектр излучения.
- •47. Оптические атомные спектры.
- •51.Виды радиоактивных излучений. Радиоактивность. Закон радиоактивного распада.
- •53. Взаимодействие рентгеновского и γ-излучений с веществом. Характеристики фотоэффекта.
- •54 Поглощённая и эквивалентная дозы.
1.Случайное событие – это событие, которое при данных условиях может произойти, либо не произойти. Относительная частота событий называется вероятностью и показывает отношение числа ожидаемых событий к числу возможных.Статистическое определение вероятности подразумевает под собой вероятность как предел, к которому стремится относительная частота. При классическом определении отн. частота и вероятность совпадают. В этом случае должно быть известно должны быть известны полное число возможных событий и число ожидаемых событий (орёл-решка, кубики и тп).Совместные события могут происходить параллельно друг другу; несовместные события исключают появление друг друга в ходе проводимого опыта. Зависимым называется событие, на вероятность которого оказывает влияние исход какого-либо иного события. Независимые наоборот.
2.Теорема сложение вероятностей: вероятность появление какого-либо события из нескольких несовместных равна сумме их вероятностей (или то, или другое)Теорема умножения вероятностей: Вероятность совместного появления независимых событий равна произведению их вероятностей(и то и другое).Условная вероятность — вероятность одного события при условии, что другое событие уже произошло(опыт с шариками в мешке, которые вытаскивают и не возвращают)
3.Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины(возможные значения которой образуют конечную или бесконечную последовательность чисел). Закон распределения может быть задан аналитически, в виде таблицы или графически. Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случ. величин оно определяется как сумма произведений случ. величины на вероятность её появления. Дисперсия описывает разброс случ. величин относительно математического ожидания. Дисперсия дискретных случ. величин определяется, как сумма квадратов разности случ. величин и математического ожидания на соответствующие вероятности появления этих случайных величин. Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.
4. Непрерывные случайные величины всегда имеют вероятность равную нулю, поскольку количество её возможных численных значений бесконечно велико.Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случ. величин оно определяется как сумма произведений случ. величины на вероятность её появления. Дисперсия описывает разброс случ. величин относительно математического ожидания. Дисперсия дискретных случ. величин определяется, как сумма квадратов разности случ. величин и математического ожидания на соответствующие вероятности появления этих случайных величин.Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.
5. Случайная величина называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Примеры:
1) дискретная случайная величина Бернулли(закон распределения Бернулли). Закон распределения дискретной случайной величины Бернулли имеет следующий вид: 0<p<1
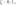

Такому распределению соответствует бросание монеты, на одной стороне которой - 0, а на второй - 1.
2) дискретная биномиальная случайная величина (биномиальное распределение). Закон распределения данной дискретной случайной величины запишется следующим образом:


где

Число успехов в n испытаниях схемы Бернулли имеет биномиальное распределение.
3) дискретная случайная величина Пуассона(пуассоновское распределение с параметром ). Закон распределения дискретной случайной величины Пуассона задается следующим образом:
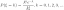 где
-
где
-
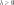 параметр.
параметр.
Закон распределения случайной величины Пуассона носит название закона редких событий, например, число вызовов, поступивших на телефонную станцию, число распавшихся нестабильных частиц и т.д.
4) дискретная геометрическая случайная величина (геометрическое распределение). Закон распределения геометрической дискретной случайной величины имеет вид

Пусть производятся независимые испытания, причем в каждом испытании возможны два исхода - "успех" с вероятностью p или "неуспех" с вероятностью 1 - p , 0 < p < 1 . Обозначим через число испытаний до первого появления "успеха", тогда будет дискретной геометрической случайной величиной.
Распределение
случайной величины называется
непрерывным,
а сама случайная величина - непрерывной
случайной величиной, если для любого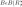
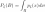 где
-
где
-
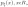 интегрируемая по Лебегу функция. Функция
интегрируемая по Лебегу функция. Функция
 называется плотностью распределения
случайной величины.
называется плотностью распределения
случайной величины.
Примеры
1) нормальная непрерывная случайная величина, или непрерывная случайная величина Гаусса(нормальное распределение).Важная роль этого распределения объясняется тем, что оно обычно возникает в явлениях, подверженных действию большого числа малых случайных величин. Так, математическая теория выборочного метода в статистике для расчета некоторых показателей широко использует нормальное распределение.
2)экспоненциальная (показательная) непрерывная случайная величина(экспоненциальное распределение).Экспоненциальному распределению подчиняется время распада ядер атомов различных элементов. Оно обладает важным свойством - отсутствием последствия. Несложно убедиться в том, что вероятность распада ядра за время при условии, что перед этим оно уже прожило время , совпадает с безусловной вероятностью распада того же самого ядра за время. Именно это свойство и представляет собой отсутствие последствия.
3) Равномерная на [a;b] непрерывная случайная величина(равномерное на отрезке [a;b] распределение).Равномерное распределение реализует принцип геометрической вероятности при бросании точки на отрезок [a;b].
Закон
Бернулли:
число ожидаемых событий, появляющихся
в опытах с n
независимыми испытаниями, в которых
ожидаемые события характеризуются
одинаковой вероятностью p
или:
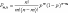
Математическое
ожидание

Пусть
 — случайная величина, определённая на
некотором вероятностном пространстве.
Тогда
— случайная величина, определённая на
некотором вероятностном пространстве.
Тогда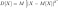 где
символ M обозначает математическое
ожидание.
где
символ M обозначает математическое
ожидание.
6. смотри билет 5
Непрерывные величины принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения. Например, время, масса, объем.Дискретные величины могут принимать конечное, счетное число случайных значений. Например, год рождения, число людей в автобусе, число страниц в книге.Распределению Пуассона удовлетворяют вероятности появления заданного кол-ва редко происходящих случайных событий, наблюдаемый в серии из большого числа независимых опытов. Это распределение описывает дискретные, целочисленные неотрицательные случайные величины, появляющиеся с вероятностью р, много меньшей 1.
Pn(m)=/m!)* ,
Где m-число ожидаемых событий, Pn(m)-вероятность появления m искомых событий в серии из n независимых испытаний, μ-параметр распределения, совпадающий с математическим ожиданием, е-основание натурального логарифма.
Формулы для вычисления математического ожидания случайной величины.
Для дискретных величин M=∑Xi * Pi
Для непрерывных величин M=
Формулы для вычисления дисперсии случайной величины, среднеквадратического отклонения
Для дискретных величин D=∑(Xi-Xср)2 * Рi
Для непрерывных величин D= 2 * f(x)dx
Среднеквадратическое отклонение δ=
Закон
распределения Пуассона:
удовлетворяет вероятности появления
заданного количества редко происходящих
случайных событий, наблюдаемых в серии
из большого количества независимых
повторных опытов. Вероятность намного
меньше 1.

Где m-число ожидаемых событий, а- параметр распределения, совпадающий с математическим ожиданием, е-основание натурального логарифма. Распределению Пуассона удовлетворяют числа редких событий, происходящих за определённый промежуток времени.
7. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое ожидание и дисперсия. Графическое представление. Примеры.
Дискретные случайные величины – величины, которые могут принимать счетное количество значений конечное или бесконечное. пример: количество пассажиров в транспорте.
Непрерывные случайные величины- величины. Которые принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения пример: время, масса, объем, температура тела.
Плотностью вероятности f(x) непрерывной случайной величины Х называется производная функции распределения F(X) этой величины: f(x)=F’(X)
Основные
свойства плотности:
1). Плотность
вероятности является неотрицательной
функцией: f(x)>0
2)
вероятность того, что в результате
испытания непрерыв. Случ. Величина
примет какое-либо значение из
интервала(а,b),
равна определенному интегралу(в пределах
от а до b
) от плотности вероятности этой случайной
величины.
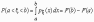
3).определенный
интеграл в пределах от минус бесконечности
до плюс бесконечности от плоности
вероятности непрерывной случайной
величины равен единице..
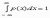
4)определенный интеграл в пределах от «–« бесконечности до х от плотности вероятности непрерывной случайной величины равен функции распределения этой величины.
Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
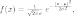
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Графики нормального распределения

Математическим
ожиданием
Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Пусть
где символ M обозначает математическое ожидание. |
8. Стандартное нормальное распределение. Стандартные интервалы. Понятия доверительного интервала и доверительной вероятности.
Доверительный интервал — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью.
Пусть
 -
выборка из некоторого распределения
с плотностью
-
выборка из некоторого распределения
с плотностью
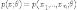 ,
зависящей от параметра
,
зависящей от параметра
 ,
который может изменяться в интервале
,
который может изменяться в интервале
 .
Пусть
.
Пусть
 -
некоторая статистика и
-
некоторая статистика и
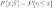 -
функция распределения случайной
величины
-
функция распределения случайной
величины
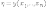 ,
когда выборка
,
когда выборка
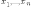 имеет
распределение с плотностью
имеет
распределение с плотностью
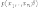 .
Предположим, что
.
Предположим, что
 есть
убывающая функция от параметра
.
Обозначим
есть
убывающая функция от параметра
.
Обозначим
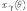 квантиль
распределения
квантиль
распределения
 ,
тогда
,
тогда
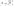 есть
возрастающая функция от
.
Зафиксируем близкое к нулю положительное
число
есть
возрастающая функция от
.
Зафиксируем близкое к нулю положительное
число
 (например,
0,05 или 0,01). Пусть
(например,
0,05 или 0,01). Пусть
 .
При каждом
неравенства
.
При каждом
неравенства
(1)
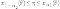
выполняются
с вероятностью
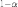 ,
близкой к единице. Перепишем неравенства
(1)
в другом виде:
,
близкой к единице. Перепишем неравенства
(1)
в другом виде:
(2)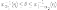
Обозначим
 ,
,
 и
запишем (2)
в следующем виде:
и
запишем (2)
в следующем виде:
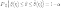
Интервал
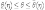 называется
доверительным
интервалом для параметра
,
а вероятность
называется
доверительным
интервалом для параметра
,
а вероятность
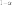 -
доверительной
вероятностью.
-
доверительной
вероятностью.
Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Графики нормального распределения
9. Понятие генеральной совокупности и выборки. Объём выборки, репрезентативность. Статистическое распределение (вариационный ряд). Примеры. Характеристики выборки
Генеральной совокупностью называют множество каких либо однородных элементов, из которого по определенному правилу выделяется некоторая часть элементов. Называемая выборкой. Число таких выделяемых объектов называется объемом выборки. Выборка производится с целью описания генеральной совокупности. Если это описание является полным и корректным, то выборка называется репрезентативной.
Пример.при анализе забол-ти детей , определенной возрастной группы, ген.совокупностью являются данные осмотра всех детей данной возрастной группы, а выборкой являютя данные, полученные в пределах одного района.
Варианта – конкретное значение случайной величины
Вариац.ряд-варианты
в определенном порядке. Вариационным
(статистическим) рядом называется
таблица, первая строка которой содержит
в порядке возрастания элементы
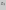 ',
а вторая - их частоты
',
а вторая - их частоты
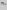 (относительные
частоты
(относительные
частоты
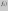 .
.
10. Оценка параметров генеральной совокупности по характеристикам её выборки (точечная и интервальная). (Параметры генеральной совокупности и характеристики выборки. Формулы, пояснения).
Интервальные оценки
По
известной величине выборочной
характеристики ( или
или
 и др.) можно определить интервал, в
котором с той или иной вероятностью
определяется значение параметра
генеральной совокупности, оцениваемого
по этой выборочной характеристике.
и др.) можно определить интервал, в
котором с той или иной вероятностью
определяется значение параметра
генеральной совокупности, оцениваемого
по этой выборочной характеристике.
Вероятности, признанные достаточными для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик, называются доверительными.
Обычно в качестве доверительных вероятностей выбирают значения 0,95, 0,99 или 0,999 (их принято выражать в процентах). Перечисленным значениям соответствуют 95, 99 и 99,9 .
5.3. Точечные оценки .
Под термином “оценка” в теории оценок понимаются как сами значения параметров генеральной совокупности, полученные по выборке, так и процесс получения этих значений, т. е. правило, по которому они получены.
Оценки подразделяются на два класса; точечные и интервальные.
Точечные оценки представляют собой определенные значения параметров генеральной совокупности, полученные по выборочным данным. Эти значения должны быть максимально близки к значениям соответствующих параметров генеральной совокупности, которые являются истинными значениями оцениваемых параметров.
ряд требований:
1.
Состоятельность.
Точечная оценка В
называется
состоятельной, если при неограниченном
увеличении объема выборки ( )
она стремится к истинному значению
параметра .
)
она стремится к истинному значению
параметра .
2. Несмещенность. Оценка В называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра .
3. Эффективность. Несмещенная оценка является эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками того же параметра генеральной совокупности.
Параметры генеральной совокупности: дисперсия и матем. Ожидание.
11. Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя).
Медиа́на (50-й процентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Полигоном
частот называют ломаную линию, отрезки
которой соединяют точки
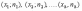 .
Для построения полигона частот на оси
абсцисс откладывают варианты
.
Для построения полигона частот на оси
абсцисс откладывают варианты
 ,
а на оси ординат – соответствующие им
частоты
,
а на оси ординат – соответствующие им
частоты
 и
соединяют точки
и
соединяют точки
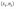 отрезками
прямых.
отрезками
прямых.
Полигон
относительных частот строится аналогично,
за исключением того, что на оси ординат
откладываются относительные частоты
 .
.
В
случае непрерывного признака строится
гистограмма, для чего интервал, в котором
заключены все наблюдаемые значения
признака, разбивают на несколько
частичных интервалов длиной h и находят
для каждого частичного интервала
 –
сумму частот вариант, попавших в i–й
интервал.
–
сумму частот вариант, попавших в i–й
интервал.
Гистограммой
частот называют ступенчатую фигуру,
состоящую из прямоугольников, основаниями
которой служат частичные интервалы
длиною h, а высоты равны отношению
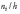 .
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го прямоугольника равна
.
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го прямоугольника равна
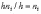 –
сумме частот вариант i–о интервала,
поэтому площадь гистограммы частот
равна сумме всех частот, т.е. объему
выборки.
–
сумме частот вариант i–о интервала,
поэтому площадь гистограммы частот
равна сумме всех частот, т.е. объему
выборки.

Модой
случайной величины называется её
наиболее вероятное значение. Термин
«наиболее вероятное значение», строго
говоря, применим только к прерывным
величинам; для непрерывной величины
модой является то значение, в котором
плотность вероятности максимальна.
Условимся обозначать моду буквой
 .
На рис. 5.6.1 и 5.6.2 показана мода соответственно
для прерывной и непрерывной случайных
величин.
.
На рис. 5.6.1 и 5.6.2 показана мода соответственно
для прерывной и непрерывной случайных
величин.

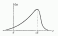
Рис. 5.6.1
В
качестве точечной оценки для “a” берут
выборочную среднюю
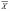 .
.
Def:
выборочной средней
 называется
среднее арифметическое выборки.
называется
среднее арифметическое выборки.
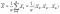 (2)
(2)
Теорема:
выборочная средняя является состоятельной
и несмещенной оценкой математического
ожидания
 .
.
12)Прямые измерения-числовые значения искомой величины получаются сравнением её с мерой(температура,длина,расстояние).
Косвенные-сводятся к нахождению значения искомой величины по известной зависимости между нею и измеренными величинами.
Погрешность-количественная х-ка качества измерения.
Абсолютная погрешность(дельта х)-разность между результатом измерения и истиным значением измеряемой величины.
дельта х=х-х0.
Относит.погрешность(Е)
Е=дельта х/х0*100%
Систематич. погрешности сохраняют постоянное значение или изменяются по известному закону в ходе измерения.
Пример:уличный термометр(дельта х=3 градусаС)
Чаще всего к систематич. относят приборные погрешности(инструментальные).Они обусловлены особенностью самого измерит. средства и его характеристиками(цена деления прибора).
Грубые погрешности(промахи)-возникают при резких изменениях условий измерений или ошибках самого оператора.(дельта t=1 час)
Пример:37.1,37.0,39.9,36.9,37.1
Результат грубой погрешности приводит к резкому отличию данных.
Случ. погр.-имеются при всех измерениях и явл. следствием случ. статических процессов в измерительном средстве или объекте измерения. Проявляются только тогда,когда измерит. средства обеспеч. достаточно высокую точность.Они имеют случайные по величине и знаку значения.
13. 13. Оценка систематической (приборной) погрешности. При прямых измерениях значение измеряемой величины отсчитывается непосредственно по шкале измерительного прибора. Ошибка в отсчете может достигать нескольких десятых долей деления шкалы. Обычно при таких измерениях величину систематической погрешности считают равной половине цены деления шкалы измерительного прибора. Например, при измерении штангенциркулем с ценой деления 0,05 мм величина приборной погрешности измерения принимают равной 0,025 мм.
Систематические
погрешности возникают и при использовании
постоянных величин, определяемых из
таблиц. В подобных случаях погрешность
принимается равной половине последнего
значащего разряда. Например, если в
таблице значение плотности стали дается
величиной, равной 7,9∙103
кг/м3,
то абсолютная погрешность в этом случае
равна
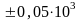 кг/м3.
кг/м3.
При
определении систематической (приборной)
погрешности косвенных измерений
функциональной величины
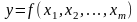 используется
формула
используется
формула
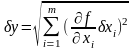 ,
(1)
,
(1)
где
 - приборные ошибки прямых измерений
величины
- приборные ошибки прямых измерений
величины
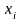 ,
,
 -
частные производные функции по переменной
.
-
частные производные функции по переменной
.
В качестве примера, получим формулу для расчета систематической погрешности при измерении объема цилиндра. Формула вычисления объема цилиндра имеет вид
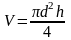 .
.
Частные производные по переменным d и h будут равны
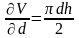 ,
,

 .
.
Таким образом, формула для определения абсолютной систематической погрешности при измерении объема цилиндра в соответствии с (2. ..) имеет следующий вид
 ,
,
где
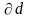 и
и
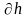 приборные
ошибки при измерении диаметра и высоты
цилиндра.
приборные
ошибки при измерении диаметра и высоты
цилиндра.
Оценка случайной погрешности.

Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.
1)погрешности измерений могут принимать непрерывный ряд значений;
2)при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
3)чем больше величина случайной погрешности, тем меньше вероятность ее появления.
График нормального закона распределения Гаусса представлен на рисунке Уравнение кривой имеет вид
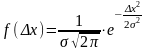 ,
,
где
 - функция распределения случайных
ошибок (погрешностей), характеризующая
вероятность появления ошибки
- функция распределения случайных
ошибок (погрешностей), характеризующая
вероятность появления ошибки
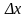 ,
σ
– средняя квадратичная ошибка.
,
σ
– средняя квадратичная ошибка.
Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное
значение средней квадратичной ошибки
σ,
как и истинное значение измеряемой
величины, неизвестно. Существует так
называемая статистическая оценка этого
параметра, в соответствии с которой
средняя квадратичная ошибка равняется
средней квадратичной ошибке среднего
арифметического
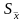 .
Величина которой определяется по
формуле
.
Величина которой определяется по
формуле
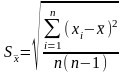 ,
(3)
,
(3)
где
- результат i-го
измерения;
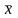 -
среднее арифметическое полученных
значений; n
–
число измерений.
-
среднее арифметическое полученных
значений; n
–
число измерений.
Чем
больше число измерений, тем меньше
и тем больше оно приближается к σ.
Если истинное значение измеряемой
величины μ,
ее среднее арифметическое значение,
полученное в результате измерений
,
а случайная абсолютная погрешность
,
то результат измерений запишется в
виде
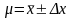 .
.
Интервал
значений от
 до
до
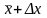 ,
в который попадает истинное значение
измеряемой величины μ,
называется доверительным
интервалом.
Поскольку
является случайной величиной, то
истинное значение попадает в доверительный
интервал с вероятностью α,
которая называется доверительной
вероятностью,
или надежностью
измерений.
Эта величина численно равна площади
заштрихованной криволинейной трапеции.
,
в который попадает истинное значение
измеряемой величины μ,
называется доверительным
интервалом.
Поскольку
является случайной величиной, то
истинное значение попадает в доверительный
интервал с вероятностью α,
которая называется доверительной
вероятностью,
или надежностью
измерений.
Эта величина численно равна площади
заштрихованной криволинейной трапеции.
Все
это справедливо для достаточно большого
числа измерений, когда
близка к σ.
Для отыскания доверительного интервала
и доверительной вероятности при
небольшом числе измерений, с которым
мы имеем дело в ходе выполнения
лабораторных работ, используется
распределение
вероятностей Стьюдента. Это
распределение вероятностей случайной
величины
 ,
называемой коэффициентом
Стьюдента,
дает значение доверительного интервала
в долях средней квадратичной ошибки
среднего арифметического
.
,
называемой коэффициентом
Стьюдента,
дает значение доверительного интервала
в долях средней квадратичной ошибки
среднего арифметического
.
 .
(4)
.
(4)
Распределение вероятностей этой величины не зависит от σ2, а существенно зависит от числа опытов n. С увеличением числа опытов nраспределение Стьюдента стремится к распределению Гаусса.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции вычисляют по формуле
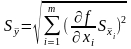 .
(5)
.
(5)
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.
1. Механические волны – процесс распространения механических колебаний в среде (жидкой, твердой, газообразной). механические волны переносят энергию, форму, но не переносят массу.Различают два вида механических волн: поперечные и продольные.Уравнение плоской волны:S=Acos [w(t-x/v),где(t-x/v)-фаза.Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении.Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), (с)Частота — число колебаний в единицу времени, (Гц, с−1).Угловая частота, круговая частота, число полных колебаний, совершающихся при периодическом колебательном процессе за 2p единиц времени.Скорость волны — скорость перемещения гребня волны в направлении ее распространения.начальная фаза, то есть фаза, с которой начинаются колебания.Фаза - это величина, которая характеризует состояние колеблющегося тела в некоторый момент времени - его положение и направление движения.
2. Звук— упругие волны, распространяющиеся в какой-либо упругой среде и создающие в ней механические колебания.Виды звуков:1)Тон-звук представляющий колебания с постоянной или закономерно изменяющейся по времени частотой.Процесс периодический. Тон может быть простым и сложным. Простой тон может быть получен с помощью камертона или звукового генератора. Сложный тон может быть разложен на простые.2)Шум-хаотический набор звуковых волн, отличающихся сложной неповторяющейся временной зависимостью(треск,скрип)
3)звуковой удар-кратковременное звуковое воздействие. Важной характеристикой звука является акустический спектр-набор частот с указанием их относительной интенсивности.
Для
плоской звуковой волны давление связано
с интенсивностью: 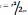 ,где -плотность среды, с- скорость звука
в данной среде.
,где -плотность среды, с- скорость звука
в данной среде.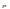 -акустический
импеданс или волновое
сопротивление.
-акустический
импеданс или волновое
сопротивление.
Интенсивность падающей волны - I1, интенсивность преломленной волны – I2. Отношение I2/ I1= В называют коэффициент проникновения звуковой волны.
3. Обьективные хар-ки звука:
1.поток энергии звуковой волны [Ф]=[Вт]
2.сила звука или интенсивность звуковой волны [I]=[Вт/м2]
3.звуковое
или акустическое давление-
максимальное
добавочное давление(избыточное над
среднем давлением окр.среды), образующееся
в участках сгущения частиц в звуковой
волне. [ ]=[Па]=[Н/м2].
]=[Па]=[Н/м2].
Для
плоской звуковой волны давление связано
с интенсивностью: 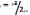 ,где -плотность среды, с- скорость звука
в данной среде.
,где -плотность среды, с- скорость звука
в данной среде.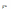 -акустический
импеданс или волновое сопротивление.
-акустический
импеданс или волновое сопротивление.
4.Эффект
Доплера
- изменение частоты и длины волн,
регистрируемых приёмником, вызванное
движением их источника и/или движением
приёмника .Для волн (например, звука),
распространяющихся в какой-либо среде,
нужно принимать во внимание движение,
как источника, так и приёмника волн
относительно этой среды. Для
электромагнитных волн (например, света),
для распространения которых не нужна
никакая среда, в вакууме имеет значение
только относительное движение источника
и приёмника. Если источник волн движется
относительно среды, то расстояние между
гребнями волн (длина волны) зависит от
скорости и направления движения. Если
источник движется по направлению к
приёмнику, то есть догоняет испускаемую
им волну, то длина волны уменьшается,
если удаляется - длина волны увеличивается:
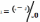 где ω0 -частота, с которой источник
испускает волны, c — скорость
распространения волн в среде, -скорость
источника волн относительно среды
(положительная, если источник приближается
к приёмнику и отрицательная, если
удаляется)Частота, регистрируемая
неподвижным приёмником.
где ω0 -частота, с которой источник
испускает волны, c — скорость
распространения волн в среде, -скорость
источника волн относительно среды
(положительная, если источник приближается
к приёмнику и отрицательная, если
удаляется)Частота, регистрируемая
неподвижным приёмником.
5. Упругие колебания частота, которых превышает 20 кГц, распространяющиеся в форме продольных волн в различных средах- ультразвук. Уз волна состоит из чередуюцихся участков сгущения и разряжения частиц.
В физиотерапии обычно применяют уз волны частотой 0,8-3 Мгц; при распространении в воде (с=1497м/с) уз-ка частотой (ню=0,88МГц) длина волны (λ=1,7мм). Важной физич. характеристикой уз явл. Амплитуда волны – максимальное смещение колеблющихся частиц среды от положения равновесия. Скорость, с которой частицы среды колеблются около среднего положения равновесия – колебательная.
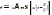 .
.
Важный
параметр- скорость
распространения уз-энергии в среде.
Колебательное движение передается от
1ой частицы к другой не мгновенно, а с
некоторой  .
Поэтому уз-волны в тканях ор-ма
распространяются с конечной
определяющейся упругими св-вами среды
и ее плотностью.
уз в жидкостях и тв телах значительно
выше чем в воздухе, где она ~330м/с
.
Поэтому уз-волны в тканях ор-ма
распространяются с конечной
определяющейся упругими св-вами среды
и ее плотностью.
уз в жидкостях и тв телах значительно
выше чем в воздухе, где она ~330м/с
Уз оказывает на ор-м механическое, тепловое и физикохимическое воздействие.
Уз терапевтический аппарат:
В аппаратах предусмотрена возможность работы в непрерывном и импульсном режимах частота следования импульсов в отечественных аппаратах 50Гц. Длительность периода (импульс+пауза) всегдасоставляет 20мс.длительность может варьировать.
6. Идеа́льная жи́дкость —воображаемая (идеализированная) жидкость, в которой, в отличие от реальной жидкости, отсутствует вязкость . В идеальной жидкости отсутствует внутреннее трение, то есть, нет касательных напряжений между двумя соседними слоями.
Уравнение
Бернулли(закон):
сумма трех членов уравнения Бернулли
для любого сечения потока идеальной
жидкости есть
величина
постоянная:
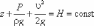
Согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Идеальная жидкость - жидкость, лишенная вязкости и теплопроводности.
1)
Условие
неразрывности струи: при
стационарном течении несжимаемой
жидкости через любые сечения трубки
тока, каждую секунду протекают одинаковые
объемы жидкости, равные произведению
площади сечения (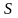 )
на среднюю скорость движения ее частиц
(
)
на среднюю скорость движения ее частиц
(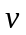 ).
).
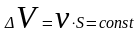 -
уравнение неразрывности струи.
-
уравнение неразрывности струи.
Если жидкость движется по системе последовательно соединенных трубок различного сечения, то скорость ее движения обратно пропорциональна площади сечения трубок (рис. 2.1).
Площадь
сечения пропорциональна квадрату
диаметра
трубки
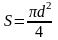 ,
поэтому
если диаметр трубки в сечении 2 вдвое
меньше,
чем в сечении 1, то площадь поперечного
сечения 2 в четыре раза меньше, чем
площадь сечения 1. Следовательно, и
скорость потока в сечении 2 будет в
четыре
раза
больше, чем в сечении 1.
,
поэтому
если диаметр трубки в сечении 2 вдвое
меньше,
чем в сечении 1, то площадь поперечного
сечения 2 в четыре раза меньше, чем
площадь сечения 1. Следовательно, и
скорость потока в сечении 2 будет в
четыре
раза
больше, чем в сечении 1.
2) Для идеальной жидкости (сила трения полностью отсутствует) справедливо уравнение, которое было получено швейцарским математиком и физиком Даниилом Бернулли. Рассмотрим тонкую трубку тока и выделим в ней два произвольных сечения (рис. 2.2).
В
общем случае эти сечения находятся на
различных высотах (h1
и h2),
и их площади различны (S1
и S2).
Вследствие уравнения неразрывности,
различны будут и скорости течения
жидкости в этих сечениях (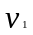 и
и
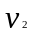 ).
Обозначим давления жидкости в этих
сечениях P1
и Р2,
соответственно.
).
Обозначим давления жидкости в этих
сечениях P1
и Р2,
соответственно.
Выделим в трубке тока малый объём жидкости ΔV, массой Δm, который перемещается из положения А в положение Б (рис. 2.2). ΔV = S1·Δl1 = S2·Δl2
Из-за малости объёма ΔV,можно считать, что сечения трубки S1 и S2 на протяжении отрезков Δl1 и Δl2 постоянны.
Перемещение массы Δm жидкости происходит под действием разности внешних сил давления в сечениях А и Б (давление Р2 противодействует движению жидкости).
Сила давления в сечении А: FP1 = P1·S1; в сечении Б: FP2 = P2·S2. FP1> FP2
За
время Δt
частицы жидкости перемещаются в сечении
А
на расстояние
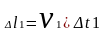 ,
в
сечении Б
на расстояние
,
в
сечении Б
на расстояние
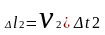
Работа
силы давления: А = FP1
·Δl1
- FP2·Δl2
=
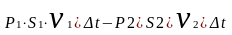 ,
,
так
как
 ,
то A
= P1·
ΔV
- P2·
ΔV
,
то A
= P1·
ΔV
- P2·
ΔV
Эта
работа затрачивается на изменение
потенциальной и кинетической энергии
массы Δm
при переходе из положения
Б
в положение
А
(из конечного вычитаем начальное)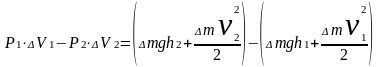 Перенесём,
все компоненты, относящиеся к сечению
А,
в левую часть уравнения, а компоненты,
относящиеся к сечению
Б
- в правую часть.
Перенесём,
все компоненты, относящиеся к сечению
А,
в левую часть уравнения, а компоненты,
относящиеся к сечению
Б
- в правую часть.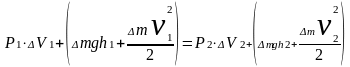 разделим
всё уравнение на ΔV,
получим:
разделим
всё уравнение на ΔV,
получим:
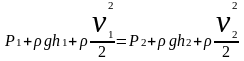 Положения
А
и Б
выбраны произвольно, значит можно
утверждать, что в любом месте вдоль
трубки сохраняется условие:
Положения
А
и Б
выбраны произвольно, значит можно
утверждать, что в любом месте вдоль
трубки сохраняется условие:
 -
это уравнение Бернулли,
-
это уравнение Бернулли,
где
Р - статическое давление, ρgh -
гидростатическое давление, обусловленное
движением жидкости, а
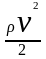 - динамическое
- динамическое
давление.
Уравнение Бернулли формулируется так: при стационарном течении идеальной жидкости полное давление, равное сумме статического, динамического и гидростатического давлений, одинаково во всех поперечных сечениях трубки тока.
7. Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
Ламинарное течение- упорядоченный режим течения вязкой жидкости (или газа), характеризующийся отсутствием перемешивания между соседними слоями жидкости.
Турбулентное течение — течение жидкости или газа, характеризующееся беспорядочным, нерегулярным перемещением его объёмов и их интенсивным перемешиванием.
Вязкость- внутреннее трение, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой.
Формула Ньютона
F=ƞ(dʋ/dx)S, где dʋ/dx- изменение скорости,S- площадь соприкосновения слоев,ƞ- динамическая вязкость жидкости.
ν=ƞ/ρ, гдеν- кинематический коэффициент вязкости, ƞ- динамическая вязкость жидкости,ρ- плотность жидкости.
Ньютоновскими называются жидкости, течение которых подчиняется уравнению Ньютона и не зависит от градиента скорости.Неньютоновскими называются жидкости, течение которых не подчиняется уравнению Ньютона. Неньютоновские жидкости- кровь, так как содержит белки и клетки крови.
Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы и определяется числом Рейнольдса: Re = pжvD/ђ
pж- плотность жидкости
D–диаметр трубы
v– средняя по сечению трубы скорость течения
ђ – динамическая вязкость
Если число Рейнольдса больше некоторого критического, то движение жидкости турбулентное. Так как число Рейнольдса зависит от вязкости и плотности жидкости. Например, для гладких цилиндрических труб Re= 2300.
Кинематическая вязкость ν является отношением динамической вязкости η к плотности жидкости ρ при той же температуре, т. е. ν = η/ρ
В качестве системной единицы измерения кинематической вязкости в СИ применяют квадратный метр на секунду (м2/сек), в системе СГС - стокс (ст); Соотношение между ними 1Ст = 10-4 м2/с.
8. Вязкость - свойство жидкости оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Ньютон установил, что сила внутреннего трения между двумя || слоями жидкости движущимися с различными скоростями зависят от ее природы и прямо пропорциональна площади S соприкосающихся слоев и градиенту скорости
d ν /dx.
Ур. Ньютона: Fтр.=ɳ*S*d ν /dx
ɳ-динамическая вязкость жидкости. ɳ=Па*с=Н/м2 *с.
Градиент скорости хар-ет быстроту изменения скорости при переходе от слоя к слою жид.т.е в направлении перпендикулярном оси трубы.
d ν /dx=ν- ν0/х-х0= ν/х.
Для характеристики вязкости жидкости используют понятие относительной вязкости жидкости, под которым понимают отношение коэф.вязкости исслед.жид. к вязкости воды. ɳотн=ɳ/ɳводы. С ↑температуры вязкость↓.
Такие жидкости называют ньютоновскими, а соотв. им вязкость- нормальной. (вода,низкомолекулярные орган.соед.) у некоторых жидкостей преимущественно высокомолекул.,коэф.вязкости зависит также от режима течения-давления и градиента скорости. Такие жидк.- неньютоновские, соотв.им вязкость аномальной.(кровь)
9.Формула стокса.
Для
сферических тел зависимость силы
сопротивления выраж.зак. Стокса. 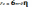 r-радиус
шарика.
r-радиус
шарика.
Ход работы-
цилиндр наполняем глицерином.(цилиндр с 2-мя кольцевыми метками
отмечаем высоту
берем стальные шарики, измеряем их диаметр.
в жидкость опускаем шарики и в определенном промежутке засекаем время.
данные вносим в табл
определяем вязкость жидкости.
n= d2tg(пл.ш-пл.ж)/18l
где.пл.ж-плотность жидкости пл.ш-плотность шарика n-вязкость(ню) d-диаметр шарика t-время g=9,8 l-высота
При движении шарика в вязкой жидкости с небольшой скоростью, когда нет вихрей, сила сопротивления:
F=6πηrν, где r - радиус шарика, ν - его скорость.
Метод Стокса.На высоком цилиндрич.сосуде с исследуемой жидкостью нанесены 2 метки: А и В на расстоянии L. А – соответствует высоте, на которой силы, действующие на шарик, уравновешивают друг друга – движение равномерное.В – для удобства подсчёта времени.Бросая шарик известной плотности р и диаметра d отмечают по секундомеру время t прохождения шариком расстояния L между метками.
Тогда вязкость жидкости опред-ся по формуле:
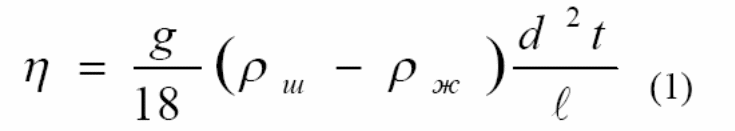
10. Коэф.Вязкости метод Оствальда.
Ход работы:
1.жидкость известной концентрации наливаем в вискозиметр и с помощью шприца поднимаем столб жидкости выше верхнего резервуара.
2.с помощью секундомера засекаем время вытекания жидкости из верхнего резервуара.
3.Проводим этот опыт 3 раза с жидкостями с концентрацией 50%, 25%, 12% и неизв. концентрацией.
4.строим график зависимости вязкости и по нему примерно определяем неизв. Концентрацию.(по оси У-вязкость, по оси Х-концентрация)
Формула вязкости по оствальду.
Vисл/Vводы =Тисл\Тводы
Где-Vисл- вязкость исследуемой жидкости
Т-время вытекания жидкости
Vисл=А*Тисл Одно колено вискозиметра – капиллярная трубка.Определенный объем жидкости вливают в широкое колено вискозиметра, а затем грушей всасывают жидкость в другое колено так, что ее уровень поднялся чуть выше отметки и далее наблюдаем понижение этого уровня ,засекая время секундомером.
Вязкость исследуемой жидкости равна=Pиссл. Жидкости * tпротекания иссл жидкости/P эталонной жидкости*tпротекания эталонной жидкости и умножить всё это на вязкость эталонной жидкости.
11.Условия применимости закона Пуазейля. Ф. Пуазейля.
Формулой Пуазейля пользуются при расчетах показателей транспортировки жидкостей и газов в трубопроводах различного назначения. Границы применимости закона Пуазейля: 1) ламинарное течение; 2) гомогенная жидкость
; 3) прямые жесткие трубки; 4) удаленное расстояние от источников возмущения.
Закон
Гагена и Пуазейля
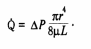 средняя скорость ламинарного течения
жидкости по круглой трубе постоянного
сечения прямопропорционально градиенту
давления X
средняя скорость ламинарного течения
жидкости по круглой трубе постоянного
сечения прямопропорционально градиенту
давления X
(где Р1иР2-давления в начале и в конце трубы длиноюl), квадрату радиуса трубы и обратна пропорциональна коэф.вязкости жидкостей.
кол-во жидкости
Ур-е Пуазейля:, можно записать: , где Х- гидравлическое сопротивление
Гидравлическое
сопротивление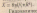 -сопротивление движению жидкости,
приводящее к потере механической
энергии потока (потери напора,
гидравлические потери).
-сопротивление движению жидкости,
приводящее к потере механической
энергии потока (потери напора,
гидравлические потери).
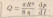
12.Последовательное
соединение.
Возьмем несколько труб различной длины,
разного диаметра и содержащих разные
местные сопротивления, и соединим их
последовательно При
подаче жидкости по такому составному
трубопроводу от точки М к
точке N расход
жидкости Q во
всех последовательно соединенных
трубах 1, 2 и 3 будет
одинаков, а полная потеря напора между
точками М и Nравна
сумме потерь напора во всех последовательно
соединенных трубах. Гидравлич.сопротивление
резко возрастает с уменьшением R
трубы. 

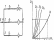 При
параллельном соединении проводников
величина, обратная общему сопротивлению
цепи, равна сумме величин, обратных
сопротивлениям параллельно включенных
труб.
При
параллельном соединении проводников
величина, обратная общему сопротивлению
цепи, равна сумме величин, обратных
сопротивлениям параллельно включенных
труб.
13..
Поверхностное натяжение
–определяется
отношением работы, затраченной на
создание некоторой пов-ти жидкости при
постоянной температуре и площади этой
пов-ти.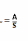 .
.
Поверхностное
натяжение равно отношению силы
пов.натяжения к длине отрезка, на котором
действует эта сила.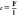 .
Пов.нат. зависит от температуры.
.
Пов.нат. зависит от температуры.
Капиллярные явления-поверхностные явления на границе жидкости с др. средой, связанные с искривлением ее пов-сти
 А)Смачивание
-вогнутый
мениск, уровень жидкости выше начального
А)Смачивание
-вогнутый
мениск, уровень жидкости выше начального
Б)Несмачивание- выпуклый мениск ,уровень жидкости меньше начального.

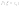 дискретной
случайной величины
дискретной
случайной величины
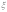 называется
сумма парных произведений всех
возможных значений случайной величины
на соответствующие им вероятности,
т.е. *
называется
сумма парных произведений всех
возможных значений случайной величины
на соответствующие им вероятности,
т.е. *
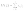
 —
случайная величина, определённая на
некотором вероятностном
пространстве.
Тогда
—
случайная величина, определённая на
некотором вероятностном
пространстве.
Тогда