2. Вибір способу реалізації

Для реалізації використано середовище програмування Qt на операційній системі Linux Ubuntu 12. Cередовище програмування Qt є актуальним, оскільки використовується в Autodesk Maya, Adobe Photoshop Elements, OPIE, Skype, VLC media player, VirtualBox, і Mathematica, і на European Space Agency, DreamWorks, Google, HP, KDE, Lucasfilm, Panasonic, Philips, Samsung, Siemens, Volvo і Walt Disney Animation Studios. Крім того, на Qt є основа середовища робочого столу KDE, графічного інтерфейсу мобільного ОС MeeGo і Qt Creator — середовища розробки на Qt при реалізації алгоритму розв’язання диференціальних рівнянь методом Ейлера використовуються процедури та функції, для того щоб скоротити витрати машинного часу при обчислюванні, та для компактності програми.

3. Дослідження системи Ресслера

Розроблено програмний продукт для розв’язування диференціальних рівнянь моделі Ресслера. В середовищі для графічного представлення використовується бібліотека OpenGL.

OpenGL — (англ. Open Graphics Library — відкрита графічна бібліотека) — специфікація, що визначає незалежний від мови програмування крос-платформовий програмний інтерфейс (API) для написання застосунків, що використовують 2D та 3D комп'ютерну графіку. Цей інтерфейс містить понад 250 функцій, які можуть використовуватися для малювання складних тривимірних сцен з простих примітивів. Широко застосовується індустрією комп'ютерних ігор і віртуальної реальності, у графічних інтерфейсах (Compiz, Clutter), при візуалізації наукових даних, в системах автоматизованого проектування тощо.

Розв’язування системи диференціальних рівнянь методом Ейлера. Зміна параметрів виконується в самому коді програми. Програмний продукт дає можливість обертати модель у програмному продукті розроблено функціонал що до повороту графічного розв’язку системи в різних напрямках. Це реалізовано кодом:

«void GLWidget::drawGear(GLuint gear, GLdouble dx, GLdouble dy, GLdouble dz, GLdouble angle) { glPushMatrix(); glTranslated(dx, dy, dz); glRotated(angle, 0.0, 0.0, 1.0); glCallList(gear); glPopMatrix(); }»

Розглянемо вплив зміни параметра µ на виникнення біфуркації в розв’язку системи взявши початкові умови На рис 2.2 представлено розв’язок при µ =8.5, інші параметри описано вище.

Рис. 2.2. Система Ресслера при µ =8.5.

На рис. 2.3 представлено графік залежності координат від часу:

Рис. 2.3. Графік залежності координат від часу при µ =8.5.

Змінимо µ. На рис. 2.4 показано який вигляд вона приймає.

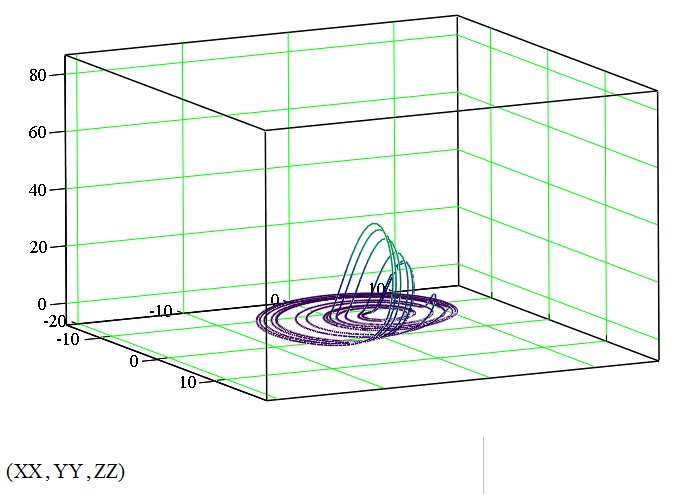
Рис. 2.4. Система Ресслера при µ =5.6.

На рис. 2.5 представлено графік залежності координат від часу:

Рис. 2.5. Графік залежності координат від часу при µ =5.6.

Змінимо µ на 4.5 На рис. 2.6 показано який вигляд приймає атрактор.

Рис. 2.6. Система Ресслера при µ =4.5.

На рис. 2.7 представлено графік залежності координат від часу:

Рис. 2.7. Графік залежності координат від часу при µ =4.5.

Змінимо µ на 3.2 На рис. 2.8 показано який вигляд приймає атрактор.

Рис. 2.8. Система Ресслера при µ =3.2.

На рис. 2.9 представлено графік залежності координат від часу:

Рис. 2.9. Графік залежності координат від часу при µ =3.2.

Змінимо µ на 2.7 На рис. 2.10 показано який вигляд приймає атрактор.

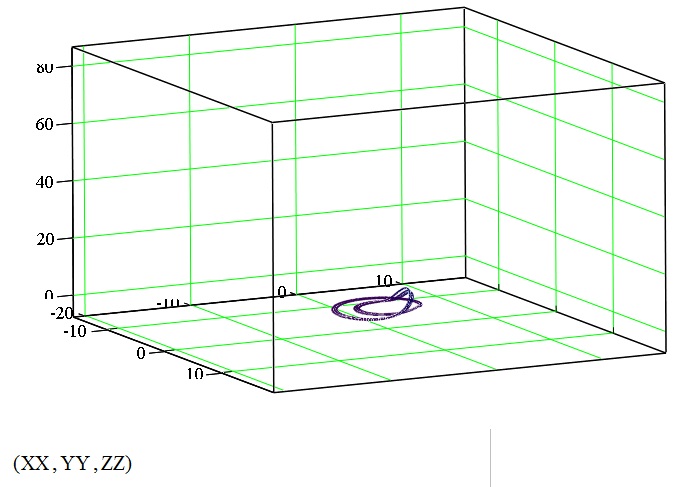
Рис. 2.10. Система Ресслера при µ =2.7.

На рис. 2.11 представлено графік залежності координат від часу:

Рис. 2.11. Графік залежності координат від часу при µ =2.7.

Текст програми приведений в Додатку А.

Проаналізувавши одержані дані можна зробити висновок, що системи з початковими умовами періодичні, а хаотичні. Це видно з графіку залежності координат від часу.