2.2 Расчет углов поворотов в опорах

Для определения угловых перемещений в сечениях C и B приложим в этих сечениях единичные моменты M=1 ( ). Получим единичные состояния (рисунок 7 а, б и 8 а, б). Построим для этих состояний эпюры изгибающих моментов и (рисунок 7 в,г и 8 в,г).

Построим грузовые эпюры и (рисунок 7 д,е и 8 д,е).

2.2.1 Расчет углов поворотов в опорах в вертикальной плоскости

Разобьем эпюру изгибающих моментов (рисунок 7д) на элементарные фигуры, площади которых обозначим через , , и (рисунок 7 д).

Определим положения центров тяжести фигур (рисунок 7д) обозначив их , , и . Вычислим значения ординат взятых по центрам тяжести , , и (рисунок 7 д) на эпюрах и (рисунок 7 в,г).

Причем для :

- индекс j соответствует номеру «единичного» состояния (для эпюры j=3, а для эпюры j=4)

- индекс i – соответствует номеру фигуры (на эпюре .четыре элементарные фигуры, следовательно i=1,2,3,4).

Значения площадей , , и были вычислены ранее табл. 1

Занесем полученные значения и в таблицу 6

Таблица 6 – Рассчитанные значения

№ фигур i	Площадь фигур , Нм2	Ордината м
		Номер состояния j
		3	4
1	60	0	0
2	310,5	0,0784	0,0323
3	92,547	0,0118	0,1323
4	49,14	0	0

Найдем углы поворота балки по формулам:

(25)

(26)

Вычитание в квадратных скобках осуществляется когда эпюра ЭМу (рисунок 7д) принимает отрицательные значения, в данном случае эпюра на всем протяжении положительна кроме участков с площадью фигуры и .

Подставим значения:

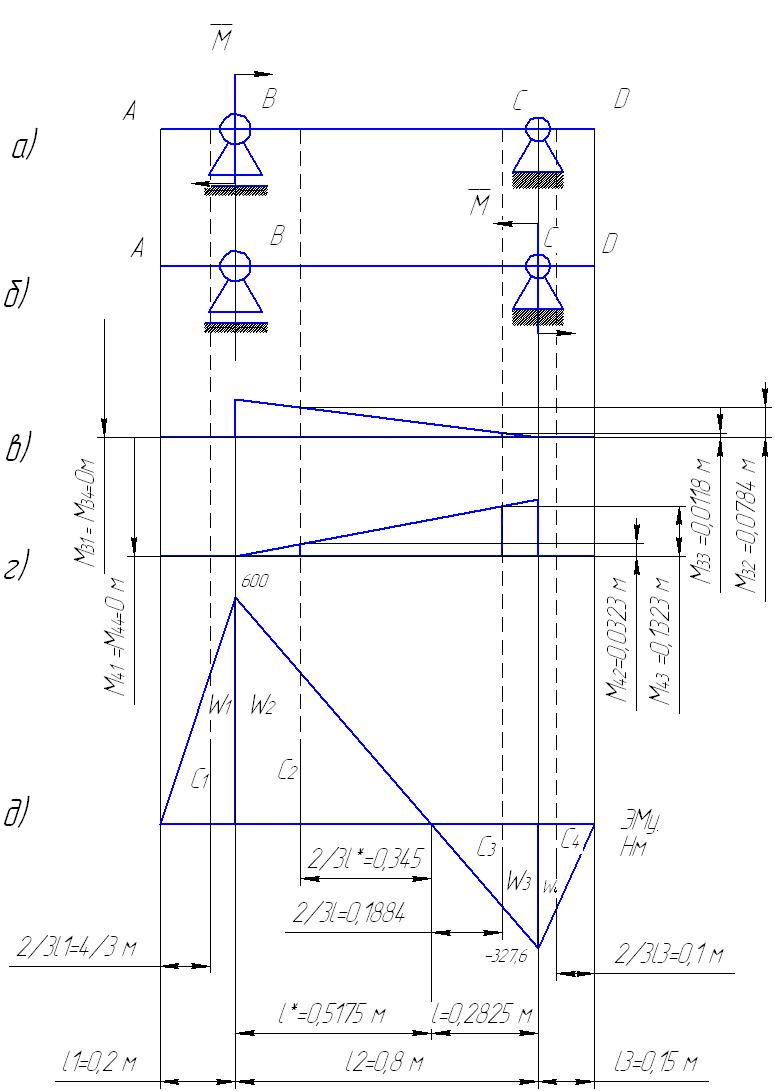
Рисунок 7 – Эпюры определения углов поворота в вертикальной плоскости

2.1.2 Расчет прогибов вала в горизонтальной плоскости

Разобьем эпюру изгибающих моментов (рисунок 8 д) на элементарные фигуры, площади которых обозначим через , , , и (рисунок 8 д).

Определим положения центров тяжести фигур (рисунок 8 д) обозначив их , , , и . Вычислим значения ординат взятых по центрам тяжести , , и . (рисунок 7 д) на эпюрах и (рисунок 8 в,г).

Причем для :

- индекс j соответствует номеру «единичного» состояния (для эпюры j=3, а для эпюры j=4) ;

- индекс i – соответствует номеру фигуры (на эпюре .четыре элементарные фигуры, следовательно i=5,6,7,8,9).

Значения площадей , , и были получены ранее (таблица 2).

Занесем полученные значения и в таблицу 7.

Таблица 7 – Рассчитанные значения

№ фигур i	Площадь фигур , Нм2	Ордината м
		Номер состояния j
		3	4
5	38	0	0
6	11	0	0
7	30	0,0916	0,0126
8	270	0,0252	0,1122
9	67,5	0	0

Найдем повороты балки по формулам:

(27)

(28)

Вычитание в квадратных скобках осуществляется, когда эпюра ЭМz (рисунок 8д) принимает отрицательные значения, в данном случае эпюра на всем протяжении положительна кроме участков с площадью фигуры и .

Подставим значения:

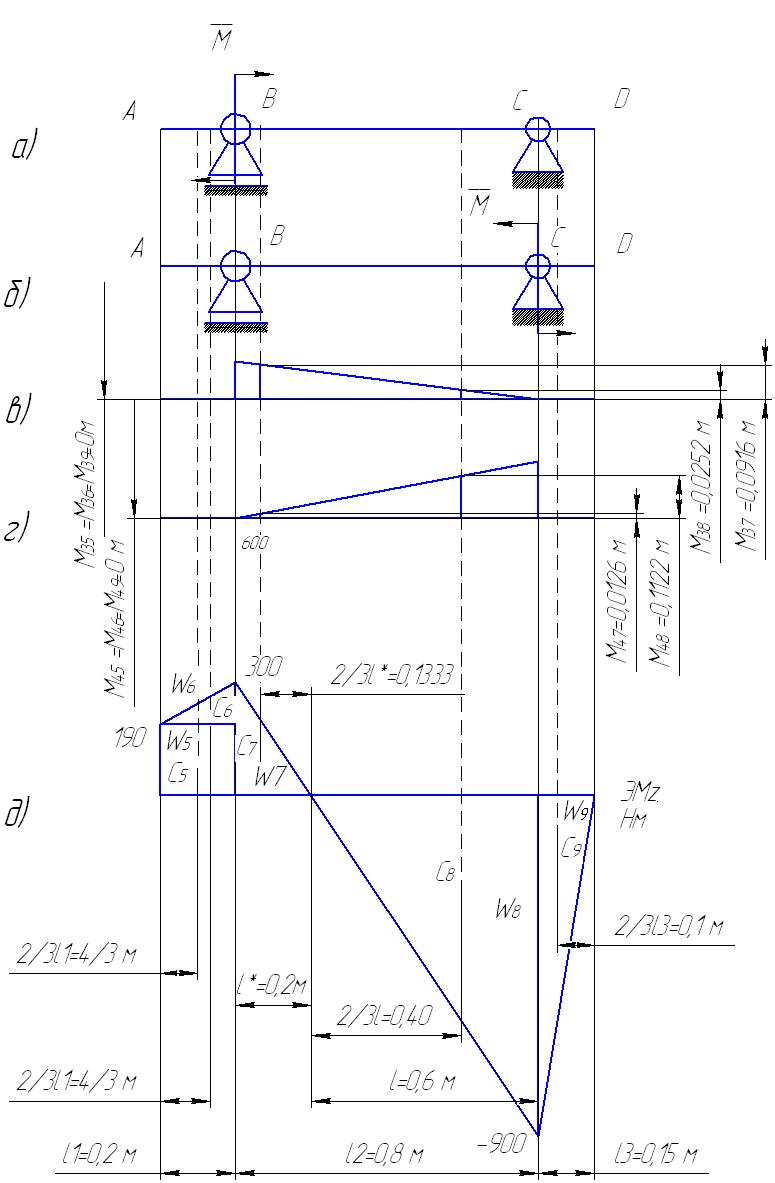
Рисунок 8– Эпюры угловых поворотов в горизонтальной плоскости

Найдем полные угловые повороты в точке С:

.

Найдем полные угловые повороты в точке В:

.