- •Проектировочный расчет вала на статическую прочность
- •1.1 Построение расчетной схемы вала
- •1.2.4 Анализ вала на изгиб в горизонтальной плоскости zox
- •1.2.5 Построение эпюры суммарных изгибающих моментов
- •1.3 Расчет диаметра вала
- •2 Расчет вала на жёсткость
- •2.1 Расчет прогибов вала в местах установки колёс
- •2.1.1 Расчет прогибов вала в вертикальной плоскости
- •2.1.2 Расчет прогибов вала в горизонтальной плоскости
- •2.2 Расчет углов поворотов в опорах
- •2.2.1 Расчет углов поворотов в опорах в вертикальной плоскости
- •2.1.2 Расчет прогибов вала в горизонтальной плоскости
- •2.3 Расчет на изгибную жесткость. Уточнение диаметров валов
- •3 Расчет вала на усталостную прочность
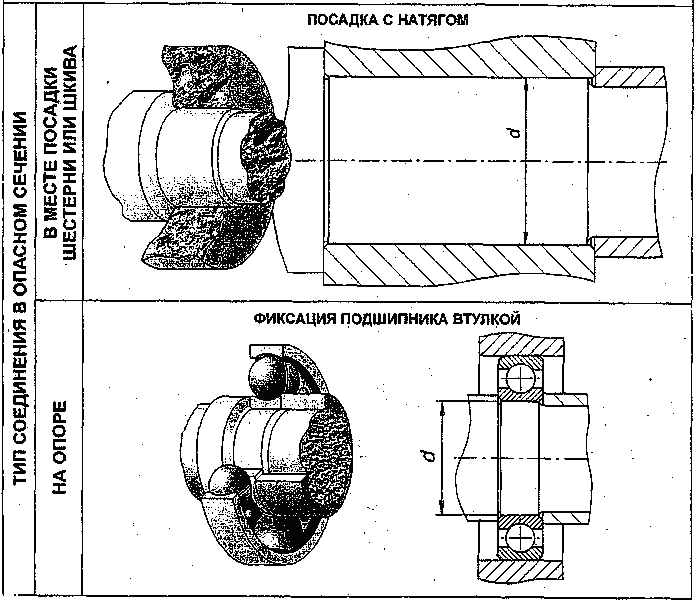
- •3.1 Выбор типа соединения в опасном сечении вала
- •3.2 Определение расчетных сечений и концентраторов напряжений
- •3.3 Расчет характеристик цикла для нормальных и касательных напряжений в расчетных сечениях
- •3.5 Расчет коэффициента запаса усталостной прочности
- •3.6 Расчет коэффициента запаса усталостной прочности. Проверка прочности
Формирование исходных данных
Шифр варианта задания состоит из четырех цифр:
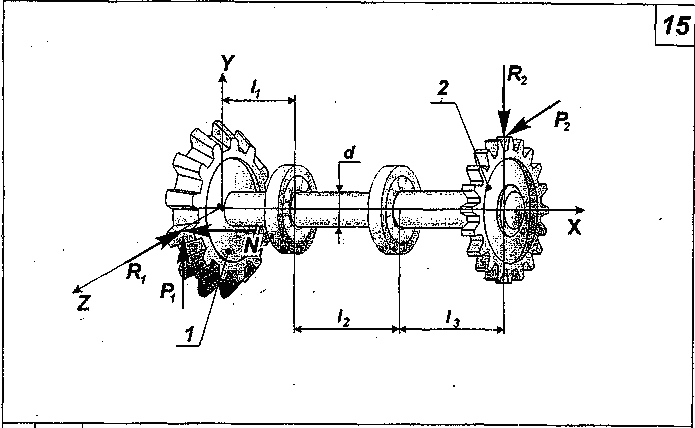
- первые две цифры соответствуют номеру расчетной схемы (Приложение II) – выбираются по порядковому номеру студента в журнале посещаемости группы принимаем 15;
- третья цифра соответствует силовым факторам (Приложение I , таблица 1, левая часть) - выбирается по последней цифре зачетной книжки, принимаем 6;
- четвертая цифра соответствует геометрическим параметрам расчетной схемы (Приложение I , таблица 1, правая часть) - выбирается по предпоследней цифре зачетной книжки. Принимаем 9.
Согласно данных соответствует шифр 15-6-9.
|
|
Рисунок 1 – Схема 15
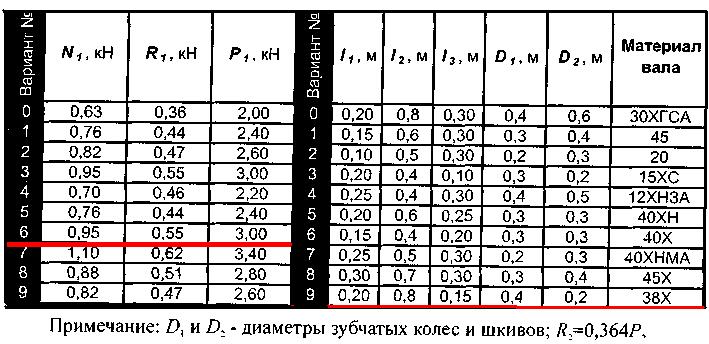
Таблица 1 – Исходные данные для расчета
Проектировочный расчет вала на статическую прочность
Согласно анализа исходных данных получены значения:
N1 = 0.95 кН = 950 Н;
R1 = 0.55 кН = 550 Н;
Р1 = 3 кН = 3000 Н;
l1 = 0.2 м, l2 = 0.8 м, l3 = 0.15 м;
D1 = 0.4 м, D2 = 0.2 м;
R2 = 0.364 Р2 ;
Материал вала (колес) сталь 38Х.
1.1 Построение расчетной схемы вала
При расчете на статическую прочность представим вал АВ в виде балки на двух опорах. Одну из опор примем шарнирно-неподвижной (сечение С), другую как наиболее близко расположенную к коническому колесу 1 ,- шарнирно-подвижной (сечение В).
Заменим действие установленных на вал колес соответствующими нагрузками. Векторы радиальных сил R1 и R2 перенесем в центр тяжести сечения вала по линии их действия. Векторы окружных сил P1 и P2 –параллельно самим себе (рисунок 2).
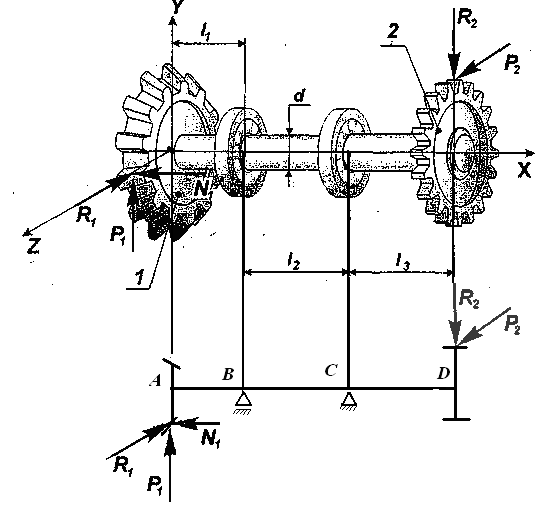
Рисунок 2 – расчетная схема
При этом появятся два крутящих момента на участке от A до D в сечениях А и D соответственно.
![]() Нм
Нм
![]() Нм
Нм
Для определения окружного усилия Р2 запишем уравнение статического равновесия в виде суммы моментов всех сил, действующих на вал, относительно продольной оси х:
![]() (1)
(1)
Откуда выразим:
![]() Н.
Н.
![]() Нм.
Нм.
Перенесем вектор силы N1 на ось вала. При этом в сечении А возникнет изгибающий момент:
![]() Нм.
Нм.
Радиальное усилие R2 найдем по формуле:
![]() Н.
Н.
Силовые
факторы, лежащие в вертикальной плоскости
YОX,
вызовут в подшипниках реакции
![]() и
и
![]() ,
а в горизонтальной ZX -
,
а в горизонтальной ZX -
![]() и
и
![]() .
.
Величины этих реакций определим, как для балки, лежащей на двух опорах.
Запишем сумму моментов относительно точек B и C в плоскости УОХ.
![]() (2)
(2)
![]() (3)
(3)
Из уравнений статистического равновесия определим RCY и RBY:
![]() Н;
Н;
![]() Н.
Н.
Проверим правильность реакций. Для этого запишем уравнения статистического равновесия в виде суммы проекций всех сил на ось у:
![]()
Значит реакции RCY и RBY найдены верно.
Запишем сумму моментов относительно точек B и C в плоскости ZОХ:
![]() (4)
(4)
![]() (5)
(5)
Из уравнений статического равновесия определим реакции в опорах С и B (RCZ и RBZ):
![]() Н
Н
![]() Н
Н
Для проверки правильности определения реакций запишем уравнения статистического равновесия в виде суммы проекций всех сил Fi на ось z:
![]() .
.
Следовательно реакции RCZ и RBZ найдены верно.
1.2 Построение эпюр внутренних силовых факторов
Видно, что вал работает на совместное действие растяжения (сжатия), кручения и изгиба в вертикальной (уох) и горизонтальной (zоx) плоскостях. Рассмотрим каждую деформацию отдельно.
Определим опасную точку вала. Для этого установим как меняются по длине вала внутренние силовые факторы, т.е. построим их эпюры.
1.2.1 Анализ вала на растяжение (сжатие)
Вал нагружен двумя сосредоточенными продольными силами: N1 и реакцией RСX=N1=950 Н. Построим эпюру нормальных сил ЭN (положительная так как происходит растяжение) на участке от А (где приложена сила N) до С (где расположена неподвижная опора С и соответственно приложена сила RСX ), (рис. 3.a).
1.2.2 Анализ вала на кручение
Два скручивающих момента Т1 и Т2 вызывают кручение на участке от А (где приложен крутящий момент Т1=600 Нм) до D (где приложен крутящий момент Т2=600 Нм. Эпюру крутящих моментов строим так же, как и при чистом кручении ЭТ,Нм (рис. 3.b).
1.2.3 Анализ вала на изгиб в вертикальной плоскости YOX
Эпюра ЭМy изгибающих моментов относительно оси y строится от сил Р1, R2, RCY и RBY, действующих в вертикальной плоскости.
Так как балка нагружена только сосредоточенными силовыми факторами, то изгибающий момент My на всех участках будет постоянен или меняться по линейному закону.
Вычислим изгибающие моменты My в сечения А, В, С и D.
Участок 0<x1 <l1
M (x1) = Р1 x1
M (0) = Р1 0 =0Нм
M (l1) = Р1 l1 =3000·0,2=600 Нм
Участок l1<x2 <l1 + l2
M (x2) = Р1 x2 – RBY (x2- l1)
M (l1) = Р1 l1– RBY (l1- l1)=3000·0,2=600 Нм
M (l1 + l2) = Р1 (l1 + l2)– RBY (l1 + l2 - l1) = Р1(l1 + l2)– RBY l2
M (l1 + l2) = 3000·(0,2+0.8) – 4159.5·0.8= -327,6Нм
Участок 0<x3 <l3
M (x2) = -R2 x3
M (0) = -R2 0=0 Нм
M (l3) = -R2 l3=-2184·0.15= -327,6Нм
В итоге получены значения в точках:
![]() Нм,
Нм,
![]() Нм,
Нм,
![]() Нм,
Нм,
![]() Нм
Нм
По полученным значениям строим эпюру ЭМy. (рис. 3.с).