27. Структурная и приведенная формы систем одновременных уравнений

Система одновременных уравнений (или струк­турная форма модели) обычно содержит эндогенные и экзоген­ные переменные.

Эндогенные переменные обозначены в системе как у. Это зависимые пере­менные, число которых равно числу уравнений в системе.

Экзогенные переменные обозначаются обычно как х. Это пре­допределенные переменные, влияющие на эндогенные перемен­ные, но не зависящие от них.

Простейшая структурная форма модели имеет вид:

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Эконо­мические переменные могут выступать в одних моделях как эн­догенные, а в других — как экзогенные переменные. Структурная форма модели позволяет увидеть влияние изме­нений любой экзогенной переменной на значения эндогенной переменной.

Структурная форма модели в правой части содержит при эн­догенных и экзогенных переменных коэффициенты b и a, которые называются структурные коэффициенты модели. Все переменные в модели выражены в от­клонениях от среднего уровня, т. е. под х подразумевается х — х , а под у — соответственно у — у. Поэтому свободный член в каждом уравнении системы отсутствует.

Использование МНК(метод наименьших квадратов) для оценивания структурных коэффи­циентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

По виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры, которой оценива­ются традиционным методом наименьших квадратов. Применяя МНК, можно оценить _ij, а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной фор­мы модели (_ij) через коэффициенты структурной модели a_j и b_i. .

Для структурной модели вида приведенная форма модели имеет вид:

в которой у₂ из первого уравнения структурной модели можно выразить следующим образом:

Приравнивая правую часть этого выражения к правой части второго уравнения системы получим: =b₂₁  y₁+a₂₂  x₂

Приводим это равенство к общему знаменателю: y₁ - a₁₁x₁ = b₁₂b₂₁y₁ + b₁₂a₂₂x₂

После приведения подобных членов получим

Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели.

Вопрос № 30. Понятие временного ряда. Компоненты временного ряда.

Эконометрическую модель можно построить, используя два типа исходных данных:

1. Данные, характеризующие совокупность различных объектов в определенный момент (период) времени. Модели, построенные по данным такого типа, называются пространственными моделями.

2. Данные, характеризующие один объект за ряд последовательных моментов (периодов) времени. Такие модели называются моделями временных рядов.

Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов (периодов) времени.

Факторы, влияющие на формирование уровней временного ряда:

1. Факторы, формирующие тенденцию ряда

2. Факторы, формирующие циклические колебания ряда

3. Случайные факторы

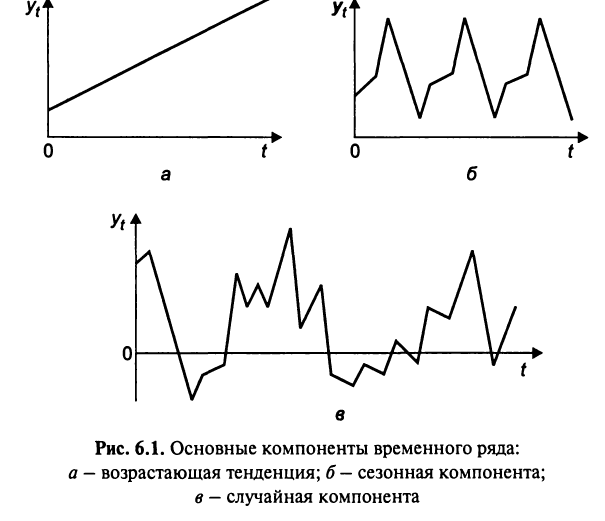
Основные компоненты временного ряда (см. Рис.):

1) а – возрастающая тенденция (в совокупности воздействие множества фактов на динамику показателя формирует либо возрастающую, либо убывающую тенденцию).

2) б – сезонная компонента (изучаемый показатель подвержен циклическим колебаниям, т.е. зависимость от времени года и т.п., например, цена на с/х продукцию в летний период выше, чем в зимний).

3) в – случайная компонента (каждый следующий уровень временного ряда образуется как сумма среднего уровня ряда и некоторой случайной компоненты (положительной или отрицательной)).

Реальные данные не соответствуют ни одной из описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.

Модели временных рядов:

• Аддитивная модель временного ряда – временной ряд представлен как сумма трендовой, циклической и случайной компонента.

• Мультипликативная модель временного ряда - временной ряд представлен как произведение трендовой, циклической и случайной компонента.

Задача эконометрических исследований отдельного временного ряда - выявление и придание количественного выражения каждой из перечисленных выше компонент для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.