Вопрос 17. Натуральная и стандартная формы модели множественной регрессии

Уравнение регрессии, построенное по исходным данным, называется моделью в натуральном виде или в натуральном масштабе. Например, множественная линейная регрессия в натуральном масштабе имеет вид:

Если провести стандартизацию переменных, входящих в модель, т.е. выполнить следующие преобразования:

а затем построить по новым переменным модель множественной линейной регрессии:

то такая модель будет называться моделью в стандартизированной форме или в стандартизированном масштабе. Стандартизированные переменные имеют среднее, равное нулю, и среднее квадратическое отклонение, равное единице. Например, для результата y имеем:

Коэффициенты модели в стандартизированной форме отличаются от коэффициентов исходной модели и поэтому обозначены другими символами – , а случайный остаток – u. Свободный член в этой модели отсутствует, что следует из свойств стандартизированной переменной и результатов применения метода наименьших квадратов (для стандартизированной формы модели свободный член равен нулю, т.к. средние всех переменных, входящих в нее, равны нулю).

18. Оценка параметров уравнения множественной регрессии и их экономическая интерпретация. Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.

Параметры уравнения множественной регрессии в задачах по эконометрике оценивают аналогично парной регрессии, методом наименьших квадратов (МНК). При применении этого метода строится система нормальных уравнений, решение которой и позволяет получать оценки параметров регрессии.

При определении параметров уравнения множественной регрессии на основе матрицы парных коэффициентов корреляции строим уравнение регрессии в стандартизованном масштабе:

в уравнении стандартизированные переменные

Применяя метод МНК к моделям множественной регрессии в стандартизованном масштабе, после опрделенных преобразований получим систему нормальных уравнений вида

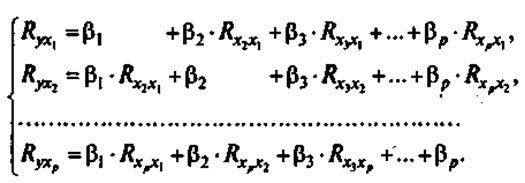
Решая системы методом определителей, находим параметры — стандартизованные коэффициенты регрессии (бета - коэффициенты). Сравнивая коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом заключается основное достоинство стандартизованных коэффициентов в отличие от обычных коэффициентов регрессии, которые несравнимы между собой.

В парной зависимости стандартизованный коэффициент регрессии связан с соответствующим коэфициентом уравнения зависимостью

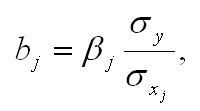
Это позволяет от уравнения в стандартизованном масштабе переходить к регрессионному уравнению в натуральном масштабе переменных:

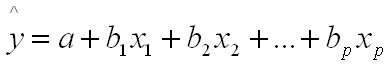
Параметр а определяется из следующего уравнения

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор xj изменится на одну сигму при неизменном среднем уровне других факторов.

(Т.е. экономический смысл параметров множественной регрессии - коэффициент множественной регрессии b_j показывает, на какую величину в среднем изменится результативный признак а, если переменную X_j увеличить на единицу измерения, т. е. является нормативным коэффициентом.)

В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии сравнимы между собой.

Рассмотренный смысл стандартизованных коэффициентов позволяет использовать их при отсеве факторов, исключая из модели факторы с наименьшим значением.

Компьютерные программы построения уравнения множественной регрессии позволяют получать либо только уравнение регрессии для исходных данных и уравнение регрессии в стандартизованном масштабе.